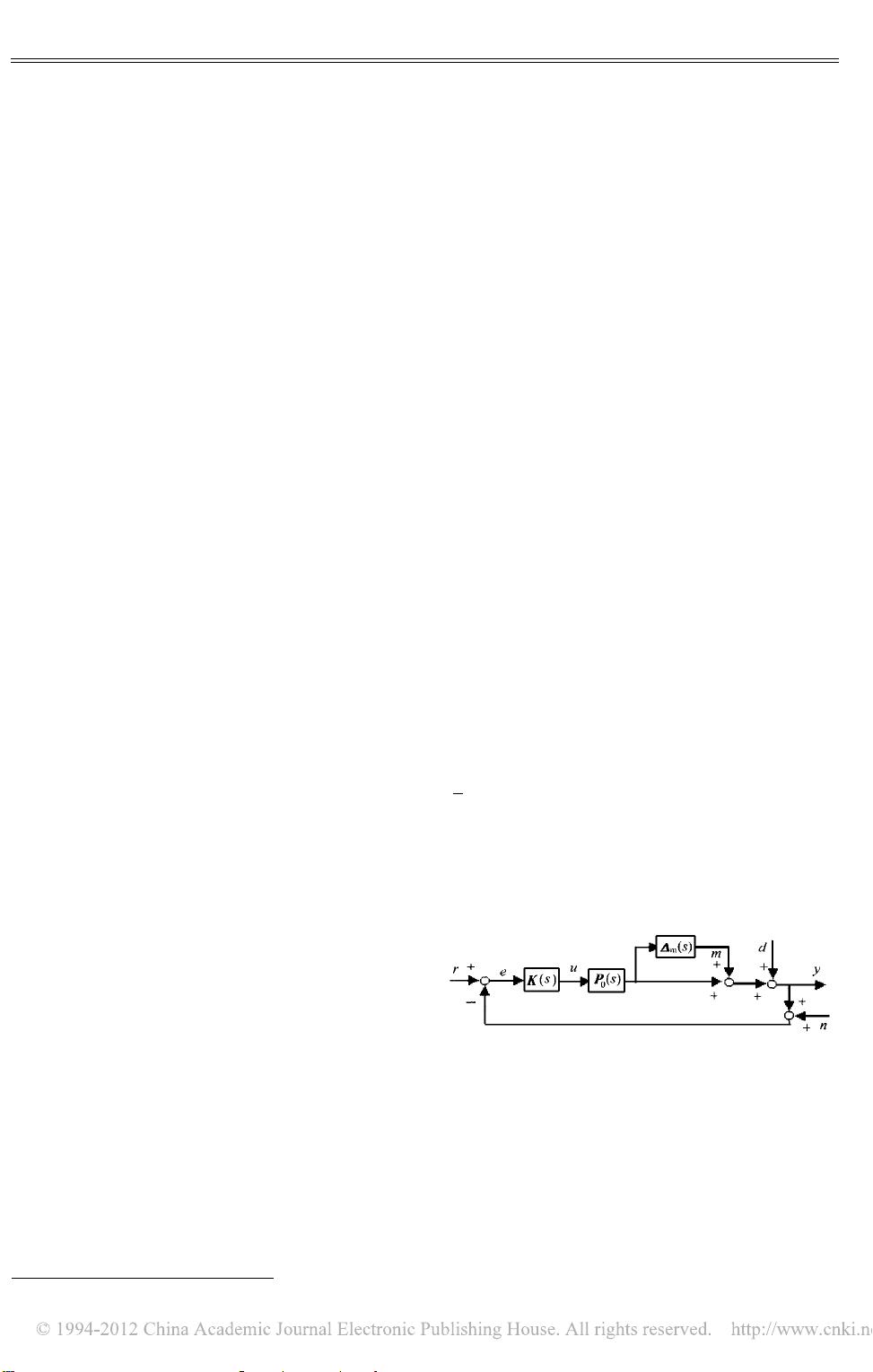
频域不确定性系统加权混合灵敏度函数频域整形

### 频域不确定性系统加权混合灵敏度函数频域整形 #### 摘要与背景 本文讨论了频域不确定性系统中加权混合灵敏度函数的设计问题，并将其应用于多变量混合灵敏度H∞控制设计中。研究的核心是解决带有输出端乘性不确定性的系统如何确定合适的加权混合灵敏度函数。通过引入一种带宽可调的加权函数频域整形方法，实现了在频域H∞控制设计中同时考虑并平衡时域和频域性能指标的目标。这种方法可以通过调整带宽来优化控制系统的性能。 #### 关键概念解释 - **频域不确定性系统**：这类系统是指在频率域内存在不确定性的动态系统，这些不确定性可能来自于系统参数的变化、未建模的动力学等。 - **鲁棒稳定性**：指控制系统在面对各种不确定性因素时仍能保持稳定性的能力。 - **加权混合灵敏度函数**：用于衡量控制系统对参考输入变化和外部扰动响应的敏感程度，通过引入加权函数来调整系统对不同频率下的信号响应。 - **带宽**：在本文中特指加权函数的有效作用范围或频率范围。 #### 技术细节 1. **频域不确定性系统分析**： - 被控对象的集合被定义为 \(M(P_0,W_m)\)，其中 \(P(s) = [I + \Delta_m(s)]P_0(s)\)，\(P_0(s)\) 是被控对象的标称模型，\(\Delta_m(s)\) 表示不确定性相对误差，\(W_m(s)\) 是稳定真有理函数，用于表示未建模动态的幅值界限。 - 鲁棒稳定性判据基于 \(M(P_0,W_m)\) 和控制器 \(K(s)\)，当 \(\Delta_m(s) = 0\) 时系统稳定，并且满足一定的条件，则系统是鲁棒稳定的。 2. **加权函数的一般化构造**： - 为了克服传统方法中对设计者经验的高度依赖性，提出了一种新的带宽可调的加权函数频域整形方法。 - 该方法提供了一个方程式构造法，可以有效地在时域和频域之间进行折衷设计。 - 通过调整带宽，可以在保证系统鲁棒稳定性的前提下，进一步优化系统的动态性能。 3. **仿真验证**： - 通过在一个双转子涡喷发动机气动热力学非线性模型上的仿真试验，验证了所提出的抗干扰性和目标跟踪性能。 - 实验结果表明，通过适当调整加权函数的带宽，可以显著提高控制系统的性能。 #### 结论 本文提出的方法为解决频域不确定性系统中的加权混合灵敏度函数设计问题提供了一种有效的解决方案。通过引入带宽可调的加权函数频域整形技术，不仅能够在频域H∞控制设计中实现时域和频域性能指标之间的平衡，还能通过调整带宽来优化控制系统的整体性能。这对于提高控制系统的鲁棒性和适应性具有重要意义。未来的研究方向可以进一步探索该方法在更广泛的实际应用场景中的适用性和效果。 #### 参考文献 - Safonov, M.G., (1988). "Multivariable Feedback Design: Concepts for a Classical/Modern Synthesis." Addison-Wesley Publishing Company. - 其他相关的文献和技术报告。 通过上述内容，我们可以清晰地理解频域不确定性系统加权混合灵敏度函数频域整形的关键概念、技术细节以及其实现目标。这种方法不仅提高了控制系统的鲁棒性和适应性，也为复杂系统控制设计提供了一种新的思路。