没有合适的资源?快使用搜索试试~ 我知道了~
近年来,线性矩阵不等式广泛应用于解决系统与控制中的一系列问题。随着解决线LMI内点法的提出以及Matlab 中LMI 控制工具箱的推广,LMI 这一工具已经受到人重视。LMI 控制工具箱已经成为了从控制工程到系统识别 设计和结构设计等诸多领域的一个强大的设计工具。由于许多控制问题都可以转化为一个LMI 系统的可行性问 题,或者是一个具有LMI约束大的徒优化问题,应用LMI来解决系统和控制问题已经成为这些领域中的一大研 究热点。
资源推荐
资源详情
资源评论

打造最优秀、专业和权威的 Matlab 技术交流平台!
http://www.matlabsky.com
近年来,线性矩阵不等式广泛应用于解决系统与控制中的一系列问题。随着解决线 LMI 内点法的提出以及 Matlab
中 LMI 控制工具箱的推广,LMI 这一工具已经受到人重视。LMI 控制工具箱已经成为了从控制工程到系统识别
设计和结构设计等诸多领域的一个强大的设计工具。由于许多控制问题都可以转化为一个 LMI 系统的可行性问
题,或者是一个具有 LMI 约束大的徒优化问题,应用 LMI 来解决系统和控制问题已经成为这些领域中的一大研
究热点。
LMI 控制工具箱,采用内点法的 LMI 求解器,这些求解器比经典的凸优化算法速度有了显著提高。另方方面,
它采用了有效的 LMI 结构化表示,在求解和计算领域做出了重大贡献。
LMI 基础知识 ......................................................................................................................................................................3
一、LMI 的一般表示 ..................................................................................................................................................3
二、描述 LMI 的相关术语 .........................................................................................................................................4
三、3 类标准的 LMI 控制问题 ..................................................................................................................................5
1.可行性问题 .......................................................................................................................................................5
2.线性目标最小化问题........................................................................................................................................5
3.广义特征值最小化问题....................................................................................................................................5
LMI 工具箱介绍和使用 ......................................................................................................................................................6
一、LMI 工具箱概述 ..................................................................................................................................................6
1.系统描述 ...........................................................................................................................................................6
2.信息检 ...............................................................................................................................................................6
3.问题求解 ...........................................................................................................................................................6
4.结果验证 ...........................................................................................................................................................6
二、LMI 工具箱函数列表 ..........................................................................................................................................8
1.确定 LMI 系统的函数 ......................................................................................................................................8
2.对 LMI 变量的操作 ..........................................................................................................................................8
3.LMI 解算器 .......................................................................................................................................................8
4.LMI 结果验证与修改 .......................................................................................................................................8
5.LMI 系统信息的提取 .......................................................................................................................................8
三、LMI 工具箱函数详解 ..........................................................................................................................................9
1.确定 LMI 系统的函数 ......................................................................................................................................9
2.对 LMI 变量的操作 ........................................................................................................................................13
3.LMI 求解器命令 .............................................................................................................................................14
4.结果验证和修改..............................................................................................................................................21
5.LMI 系统信息提取 .........................................................................................................................................24
LMI 系统实例分析 ............................................................................................................................................................25
命令行形式解答 ........................................................................................................................................................25
GUI 形式解答 ............................................................................................................................................................27
Matlab Sky

打造最优秀、专业和权威的 Matlab 技术交流平台!
http://www.matlabsky.com
LMI 基础知识
一、LMI 的一般表示
一个 LMI 就是具有形式
011
()0(1)
mm
FxFxFxF=+++<L
式
的表达式,式中的不等号表示矩阵 F(x)是【负定】的。
Tnn
ii
FFR
×
=∈ 是一组给定的是对称矩阵
i
x
是待确定的是变量,称为 LMI 系统的【决策变量】
1
[,,]
T
m
xxx
= K 以有决策变量构成的向量,成为【决策向量】
其中 i=0,1,...,m
尽管不等式(式 1)是以很基本的形式给出,然而在许多控制系统问题中,LMI 系统却很少以这样的形式给出。问
题的变量往往都是以矩阵的形式给出,例如 Lyapunov 矩阵不等式:
0(2)
T
AXXAQ++<
式
其中, ,
nn
AQR
×
∈ 是给定的常数矩阵,并且 Q 为对称矩阵,
nn
XR
×
∈
是对称的未知【矩阵变量】,下面通过一
个实例来说明不等式(式 1)和(式 2)两种形式之间的相互转化。
假设,常数
12
02
A
−
=
−
,Q 为零矩阵,变量
12
23
xx
X
xx
=
(注意 A,Q 和 X 都是对称的),那么不等式(式 2)中
的【决策变量】是【矩阵变量】X 中的独立元
123
,,
xxx
。将这个矩阵不等式写成一般形式(式 1)的时候,会得到
下面形式:
123
220300
0()
203404
xxx
−−
++<
−−
式
3
可以看出,不等式(式 3)所涉及的矩阵要比不等式(式 2)中的多。如矩阵 A 是 n 阶矩阵,那么不等式(式 3)中的系
数矩阵一般要有 n(n+1)/2 个,要占用更多的存储空间。此外,不等式(式 3)已经不再具有不等式(式 2)所具有的控
制中的直观含义,因此,LMI 工具箱中的函数一般采用线性矩阵不等式块结构来表示,并且其中每一个块都是矩
阵变量的仿射函数。
Matlab Sky
打造最优秀、专业和权威的 Matlab 技术交流平台!
http://www.matlabsky.com
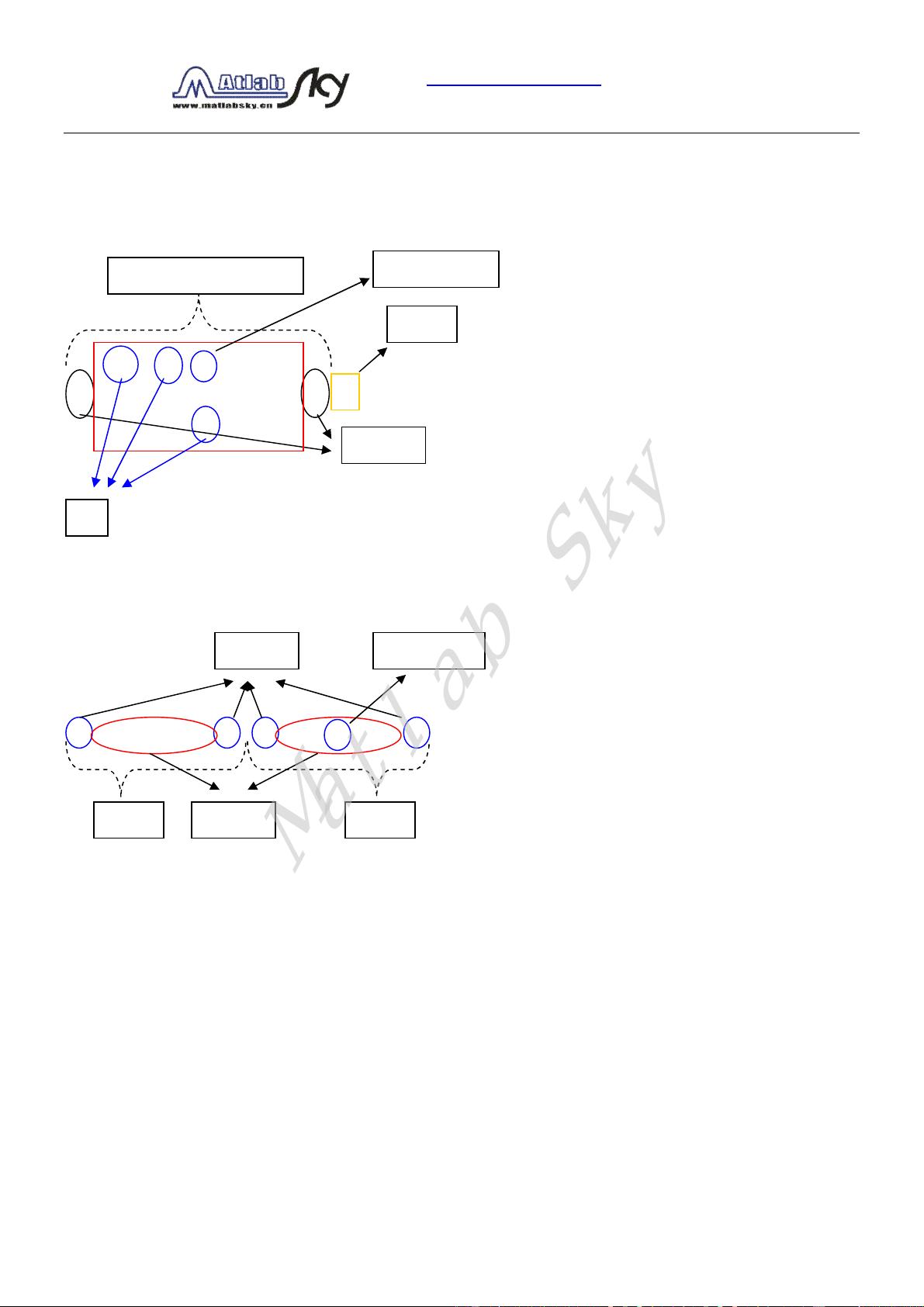
二、描述 LMI 的相关术语
以
H
∞
控制中的一个典型线性矩阵不等式为例来进行说明:
0()
TT
T
TT
AXXAXCB
NCXIDN
BDI
γ
γ
+
−<
−
式
4
其中, ,
Tnn
XXRR
γ
×
=∈∈
是上述 LMI 的【变量】,而 A、B、C、D 和 N 都是给定的【常数矩阵】。或者用更
一般形式的表示 LMI 系统
1212
(,,,)(,,,)()
TT
nn
NLXXXNMRXXXM<LL式
5
其中
k
X
是 LMI 系统的第 k 个矩阵变量或标量变量,L 和 R 是关于
k
X
的分块矩阵,N 和 M 是给定的常数矩阵。
那么我们通过下列语句来描述这个 LMI:
(1)我们约定左边是不等式较小的一边,右边是不等式较大的一边。比如 X>0,X 是不等式的右边,而 0 是右边,
也就是说 LMI 系统一般总是使用“<”号表示不等式,与优化工具箱相似。还有就是标量在 Matlab 中认为是 1
×1 的对称矩阵,例如(式 4)中的γ。
(2) (式5)中的 N 和 M 称为 LMI 的【外因子】,是具有相同维数的给定矩阵,它们可以不是方阵,在一般的问题
中都是不出现的。
(3)(式 5)中的 L 和 R,或者说不等号两边的中间位置的大分块矩阵叫做【内因子】,L 和 R 是具有相同块结构的
对称块矩阵。
(3)内因子是一个分块对称矩阵,它的分块结构是由其对角块的数目来描述的,并可完全由其对角线以上或以下
外因子
内 因 子
较小的一边,叫左边
项
右边
外因子
内因子 右边 左边
矩阵变量 X
矩阵变量
Matlab Sky

打造最优秀、专业和权威的 Matlab 技术交流平台!
http://www.matlabsky.com
的那些部分来决定,故在 Matlab 编程时,内因子只需要并且只能写出它一半。
(4)内因子中的子块矩阵中每一个表达式都称为 LMI 的【项】,它们是关于矩阵变量 X 和矩阵标量γ的仿射表达
式,并且可以分解为一些基本项之和,例如(式 4)中的内因子的第(1,1)块就包含两个基本项:
T
AX
和
XA
。
(5) 内因子中的每项都有常数项和变量项之分,所谓常数项即(式 4)中所示的 B 和 D,而变量项则至少包含一个
矩阵变量,例如
XA
以及
I
γ
−
等。
三、3 类标准的 LMI 控制问题
1.可行性问题
寻找一个
n
XR
∈
,使的满足 LMI 系统成立,这个问题的求解器为 feasp。
2.线性目标最小化问题
min
..()()
T
x
cx
stAxBx
<
此类问题的求解器为 mincx。
3.广义特征值最小化问题
min
..()()
0()
()()
x
stCxDx
Bx
AxBx
λ
λ
<
<
<
相应的求解器是 gevp。
三个解算器的功能和具体使用方法在后面会详细介绍。
Matlab Sky
剩余25页未读,继续阅读
资源评论

sinat_38097973
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- Complex-YOLO点云上的实时 3D 物体检测 pytorch Darknet.zip
- 基于HOG+SVM的行人检测,包含三个python代码和一个训练好的模型Model,两张检测图片
- 扫雷游戏的实现,运行版本
- eclipse安装包eclipse-inst-jre-win64.zip
- HCIE数通V3.0宝典全面解析路由协议
- 基于AT89S52单片机数字音乐盒的设计.ASM
- caffe 中的 YOLOv3 模型.zip
- Android流式布局-开发类似网页的热门标签
- Android Live Demo 使用 ncnn 进行 Yolov7 推理.zip
- 像写SQL一样写ORM,链式方法调用,结合Lambda,枚举 灵活适应各种情况 使用不同种类数据库的实体生成器,支持:MySQL,MongoDb,Excel,一致性的调用方法 对数据进行分组,方便
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功