图论算法理论、实现及应用 高清带书签pdf

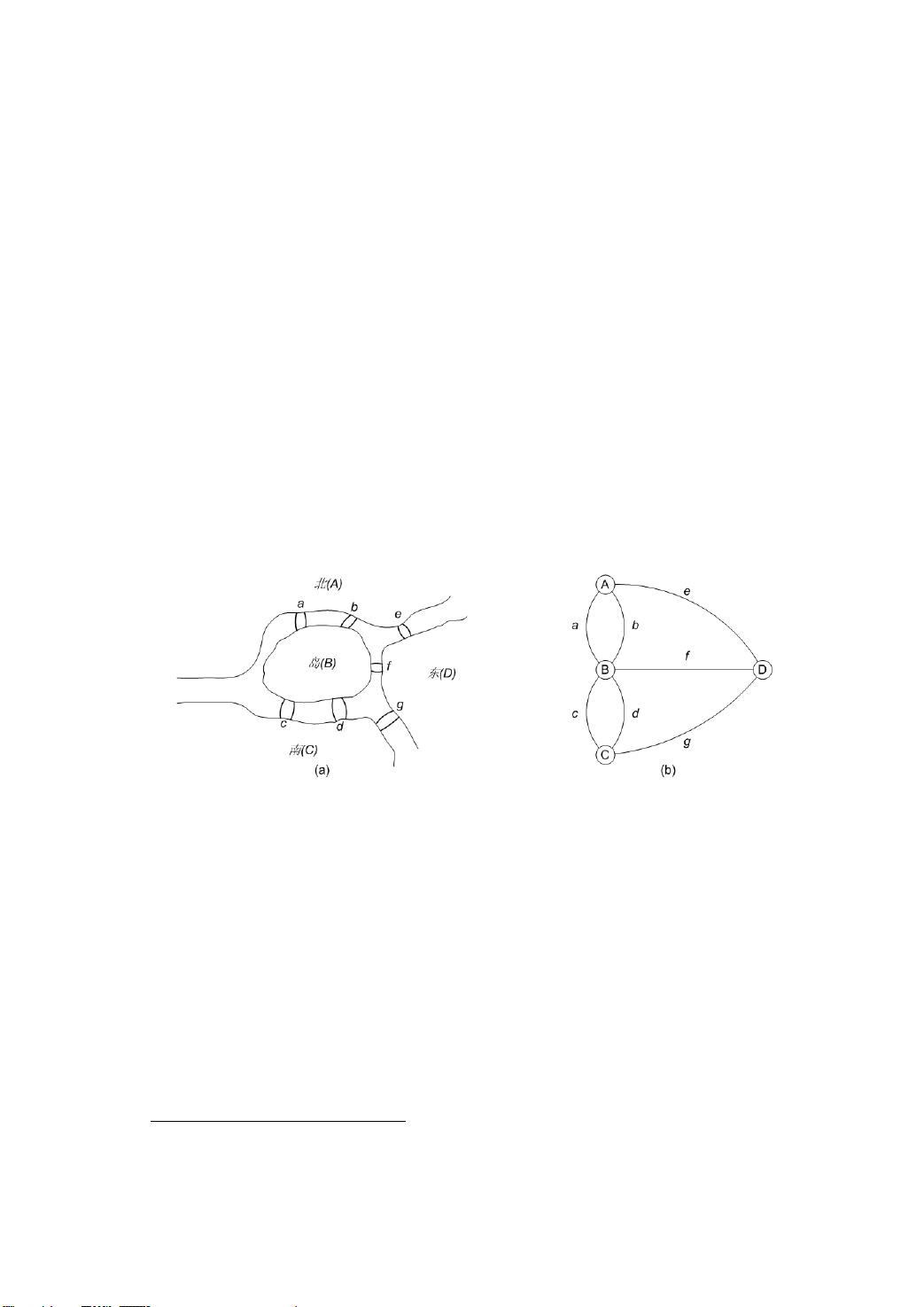
本书系统地介绍了图论算法理论，并选取经典的ACM/ICPC竞赛题目为例题阐述图论算法思想，侧重于图论算法的程序实现及应用。本书第1章介绍图论基本概念和图的两种存储表示方法：邻接矩阵和邻接表，第2～9章分别讨论图的遍历与活动网络，树与生成树问题，最短路径问题，可行遍性问题，网络流问题，点支配集、点覆盖集、点独立集、边覆盖集、边独立集(匹配)，图的连通性问题，平面图与图的着色问题等。本书可 以作为高等院校计算机(或相关专业)图论等相关课程的主教材，也可作为ACM/ICPC竞赛的辅导教材。 基本信息 书 名：图论算法理论、实现及应用 著作责任者：王桂平 王 衍 任嘉辰 标准书号：ISBN 978-7-301-17578-1/TP·1122 出 版 者：北京大学出版社 定 价：54.00元 ### 图论算法理论、实现及应用 #### 一、图论概述 图论作为数学的一个重要分支，主要研究由顶点和边组成的图形——图。这些图能够有效地表示现实世界中各种复杂的关系网络，例如社交网络、交通网络、通信网络等。通过图论的研究，不仅可以帮助我们更好地理解这些网络的特性，还能为我们提供解决实际问题的有效途径。 **1.1 基本概念** - **图(Graph)**：由顶点(Vertex)和边(Edge)组成的集合。顶点表示网络中的节点，边则表示节点之间的关系。 - **邻接矩阵(Adjacency Matrix)**：一种表示图的方式，它是一个二维数组，用于表示图中顶点之间的连接关系。 - **邻接表(Adjacency List)**：另一种表示图的方式，通过链表来存储每个顶点相邻的顶点列表。 #### 二、图论算法的核心内容 本书涵盖了多个核心章节，详细探讨了不同类型的图论问题及其解决方案。 **2.1 图的遍历与活动网络** - **深度优先搜索(DFS)**：一种遍历或搜索图中顶点的方法，从起始顶点出发，尽可能深地搜索树的分支。 - **广度优先搜索(BFS)**：另一种遍历图的方法，按层次顺序访问所有顶点。 - **活动网络**: 描述项目管理中任务间的依赖关系，常用于规划项目的完成时间。 **2.2 树与生成树问题** - **树(Tree)**：无环连通图的一种特殊形式，具有层次结构。 - **生成树(Generative Tree)**：图中包含所有顶点的最小连通子图，不包含任何环路。 **2.3 最短路径问题** - **迪杰斯特拉算法(Dijkstra's Algorithm)**：解决单源最短路径问题的经典算法。 - **弗洛伊德算法(Floyd's Algorithm)**：解决任意两点间最短路径问题的算法。 **2.4 可行遍性问题** - **连通性问题**: 确定图是否连通，即图中是否存在路径使得任意两个顶点都可以互相到达。 - **割点(Cut Vertex)** 和 **割边(Cut Edge)**：移除后会导致图不再连通的顶点和边。 **2.5 网络流问题** - **最大流算法(Maximum Flow Algorithm)**：确定网络中从源点到汇点的最大流量。 - **最小费用最大流算法(Min Cost Max Flow Algorithm)**：除了考虑流量外还考虑成本。 **2.6 点支配集、点覆盖集、点独立集、边覆盖集、边独立集(匹配)** - **点支配集(Dominating Set)**：图中的一组顶点，使得每个不在该集合中的顶点至少与集合中的一个顶点相邻。 - **点覆盖集(Vertex Cover)**：图中的一组顶点，使得图中的每条边至少与该集合中的一个顶点相连。 - **点独立集(Independent Set)**：图中没有任何两条边相邻的一组顶点。 - **边覆盖集(Edge Cover)**：图中的一组边，使得图中的每个顶点都至少被该集合中的一个边覆盖。 - **匹配(Matching)**：图中没有共享端点的边的集合。 **2.7 图的连通性问题** - **强连通图(Strongly Connected Graph)**：图中任意两个顶点之间都存在双向路径。 - **连通分量(Connected Component)**：无向图中不可再分割的连通部分。 **2.8 平面图与图的着色问题** - **平面图(Planar Graph)**：可以绘制在平面上而不发生边交叉的图。 - **图的着色问题(Graph Coloring Problem)**：给图中的顶点着色，使得相邻顶点的颜色不同，目标是最小化所需颜色的数量。 #### 三、ACM/ICPC竞赛与图论算法 **3.1 ACM/ICPC简介** ACM International Collegiate Programming Contest (ACM/ICPC)是一项全球性的大学生编程竞赛，旨在测试参赛者的算法设计、逻辑推理和编程能力。 **3.2 图论算法在ACM/ICPC中的应用** 本书通过经典的ACM/ICPC竞赛题目，展示了如何将图论算法应用于解决实际问题。通过这些例子，读者可以更好地理解算法的实际应用场景，并掌握如何在比赛中运用这些算法解决问题。 #### 四、本书的价值与适用范围 本书不仅适合高等院校计算机及相关专业的本科生和研究生作为主教材使用，也适用于希望参加ACM/ICPC竞赛的学生作为辅导教材。此外，对于从事软件开发的专业人士来说，本书也是一个非常有价值的参考资料，可以帮助他们更深入地理解和应用图论算法。