自动控制原理复习资料PPT学习教案.pptx

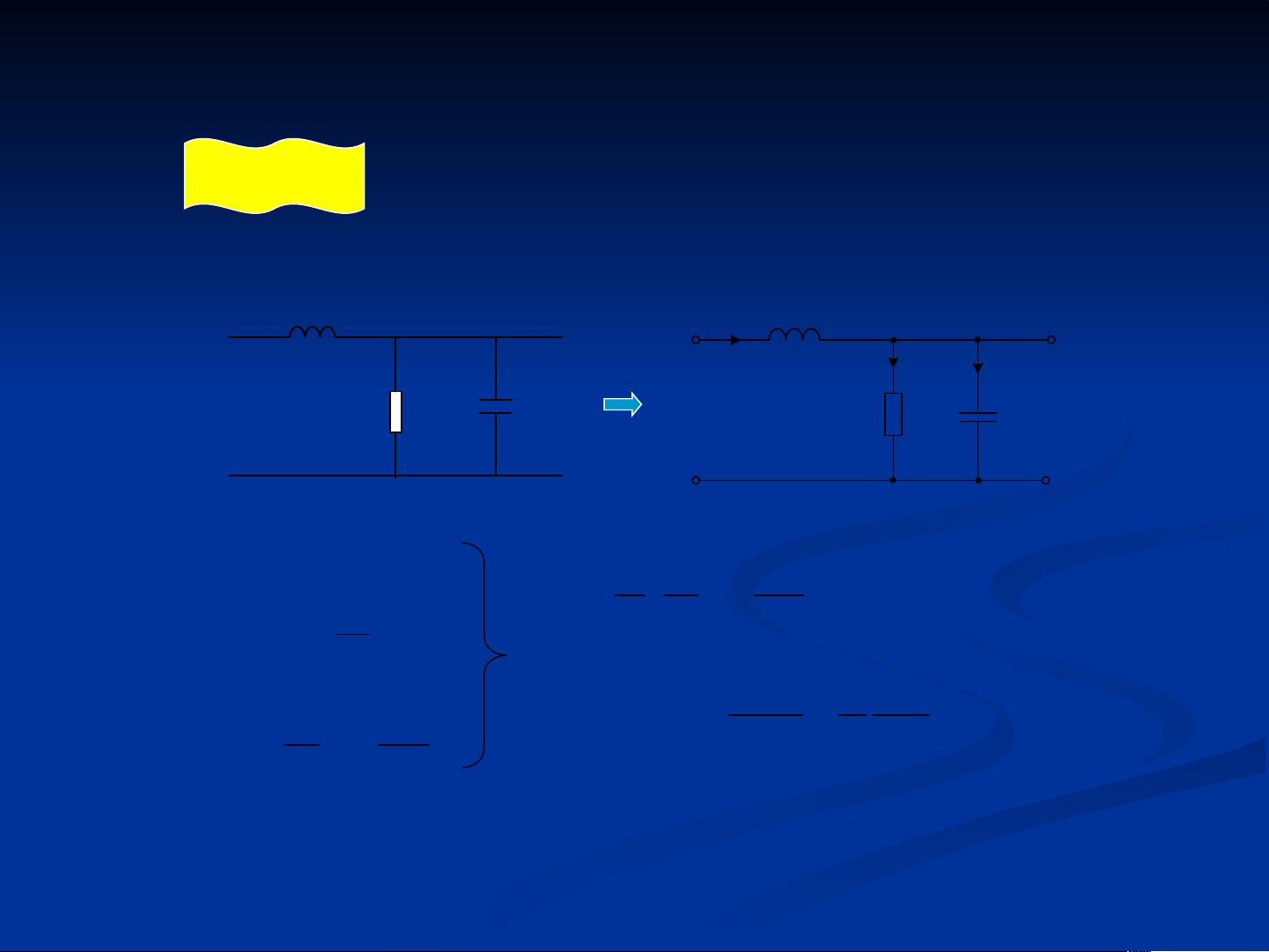
《自动控制原理复习资料》是针对自动控制领域的一份重要学习资源，主要涵盖了线性系统的数学模型、典型环节的传递函数以及如何通过微分方程和方框图来描述和分析控制系统。这份资料对于理解自动控制理论至关重要。 线性系统的数学模型是分析控制系统的基础。在电气工程中，电路系统分为无源网络和有源网络。无源网络由电阻(R)、电感(L)和电容(C)等不含电源的元件构成，而有源网络则包括运算放大器等含电源的器件。利用基尔霍夫电流定律(KCL)和电压定律(KVL)，结合元件的伏安关系，可以列出描述电路行为的微分方程。例如，理想运算放大器具有“虚短”和“虚断”的特性，这在构建微分方程时需考虑。 在处理电路系统时，可以通过列微分方程法或复阻抗法来求解传递函数。传递函数描述了系统输入与输出之间的关系，是控制系统分析的关键。例如，对于一个包含电阻、电感和电容的电路，可以通过对微分方程两边进行拉普拉斯变换，简化计算并得到传递函数的表达式。 在典型环节的传递函数部分，提到了比例环节、惯性环节、积分环节、纯微分环节以及一阶微分环节和二阶振荡环节。这些基本环节是构建复杂系统模型的基础，它们的传递函数分别具有特定的形式，例如，惯性环节的传递函数为1/(1+Ts*s)，其中T表示时间常数。 方框图方法是将系统的微分方程转化为图形化表示，便于理解和设计控制系统。绘制方框图时，需要注意每个环节的输入和输出关系，以及前向通路和反馈通路的清晰性。通过将各个典型环节组合，可以构建整个系统的传递函数方框图，从而分析系统的动态性能和稳定性。 例如，在给定的例题中，系统的微分方程被转换为一系列传递函数，然后通过方框图逐一构建，最终得到系统的总传递函数。这个过程展示了如何将复杂的动态系统分解为可管理的部分，并通过数学手段进行分析。 《自动控制原理复习资料》是学习自动控制理论的宝贵教程，涵盖了从基本的电路分析到高级的系统建模和分析技术，对于深入理解和应用控制理论至关重要。