详细的信号与系统的课件

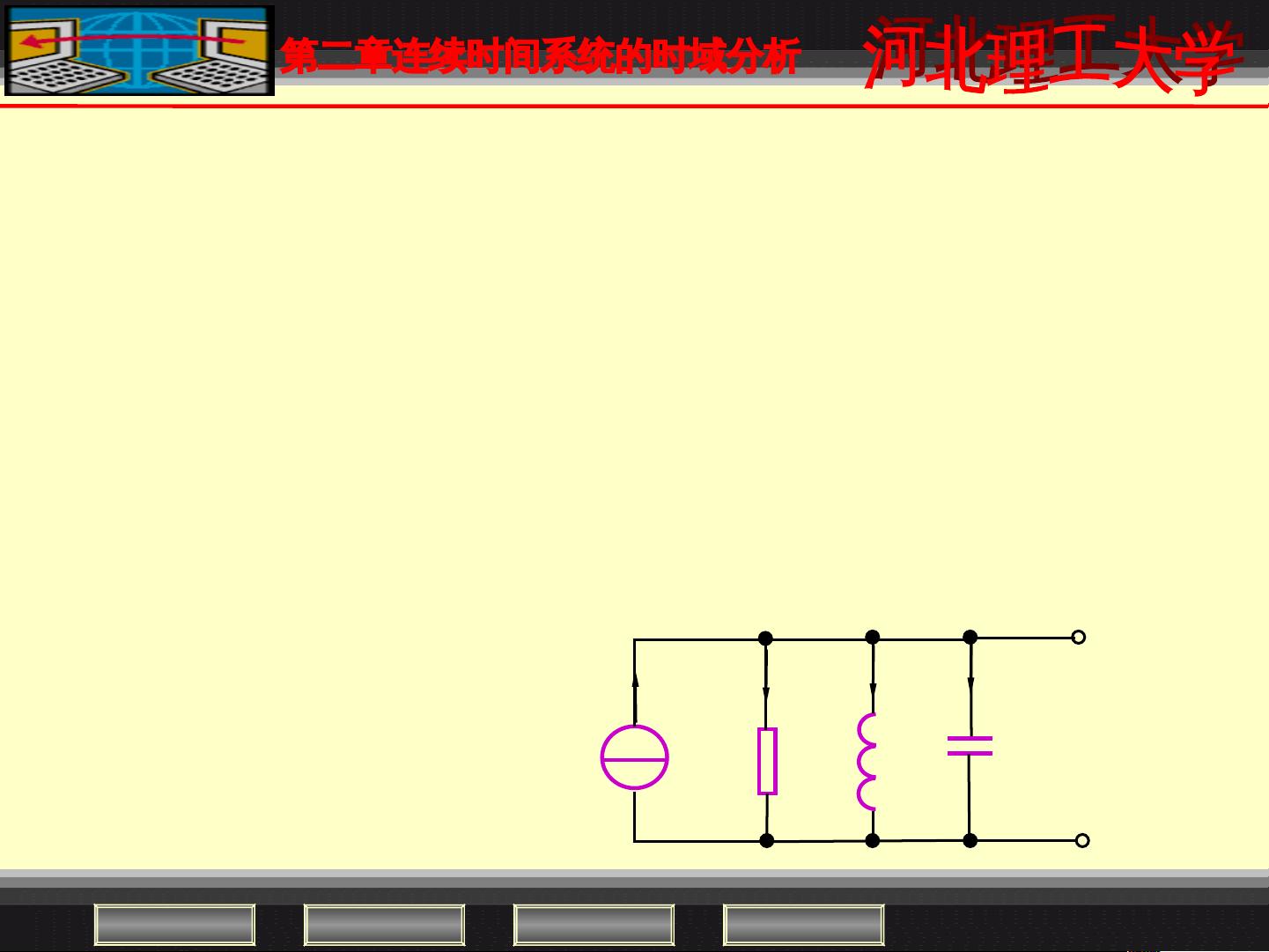
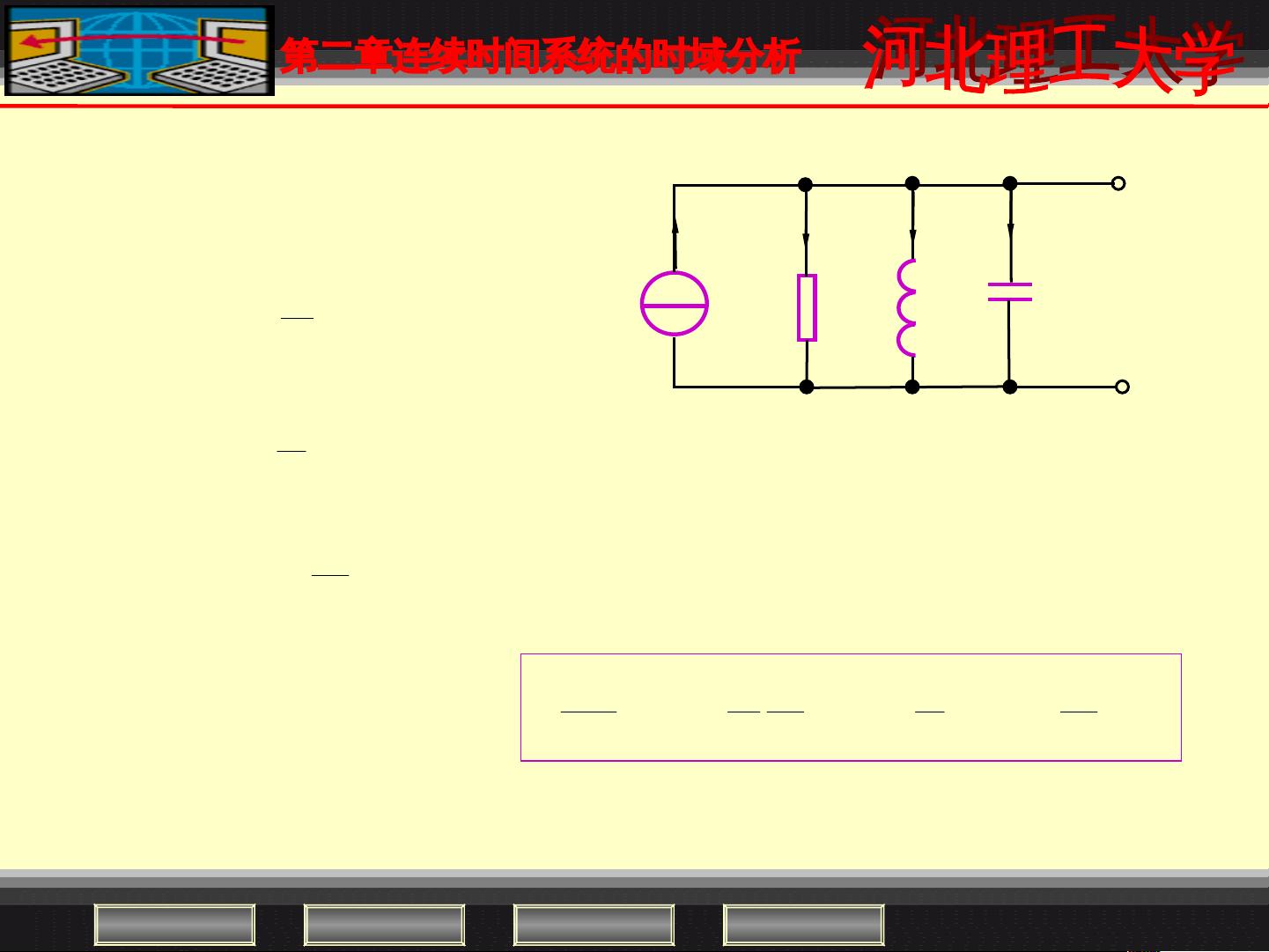
《信号与系统的详尽解析》 信号与系统是电子工程和通信领域中的核心课程，它主要研究信号的处理和传输，以及系统对这些信号的响应。在这个课件中，我们将深入探讨几个关键概念，包括微分方程的建立与求解、零输入响应和零状态响应、冲激响应与阶跃响应、卷积以及算子符号表示微分方程等。 让我们关注微分方程的建立与求解。在信号与系统中，微分方程被用来描述连续时间系统如何响应输入信号。例如，在RLC并联电路中，通过基尔霍夫电流定律（KCL）和电压定律（KVL）可以建立描述系统特性的微分方程。对于给定的物理模型，我们根据元件的特性（如电阻、电感、电容）及其相互关系，列出相应的微分方程。例如，RLC电路的微分方程可以表示为一个二阶线性常系数微分方程。 我们讨论零输入响应（ZIR）和零状态响应（ZSR）。零输入响应是指当系统在初始时刻没有外加激励时，仅由初始条件产生的系统响应；而零状态响应则是指系统在初始时刻没有储能，仅由当前输入产生的响应。这两种响应在分析线性时不变系统时尤为重要，因为它们可以分解复杂系统的行为。 接着，我们引入了冲激响应和阶跃响应的概念。冲激响应是系统对单位冲激函数的响应，反映了系统的基本动态特性。阶跃响应则是系统对阶跃输入的响应，通常用于评估系统的瞬态和稳态性能。卷积作为时域分析的核心工具，允许我们利用系统的冲激响应来计算任意输入信号下的系统输出。 卷积的性质是信号处理中的基本运算规则，它在求解线性系统的输出时起着至关重要的作用。卷积积分是连接时域分析和变换域分析的桥梁，通过将输入信号与系统的冲激响应相卷积，可以得到系统对任何输入信号的输出响应。 此外，算子符号表示微分方程是一种抽象的数学表示方法，它可以简化复杂的微分方程处理，便于进行系统分析。例如，通过引入算子L，我们可以将微分方程转化为代数方程，从而更方便地求解系统响应。 总结起来，信号与系统的研究涵盖了从基本的微分方程建立到高级的系统响应分析。理解和掌握这些概念，无论是对于理论学习还是实际工程应用，都是至关重要的。通过深入学习这个课件，你将能够更好地理解连续时间系统的时域特性，并具备解决复杂系统问题的能力。