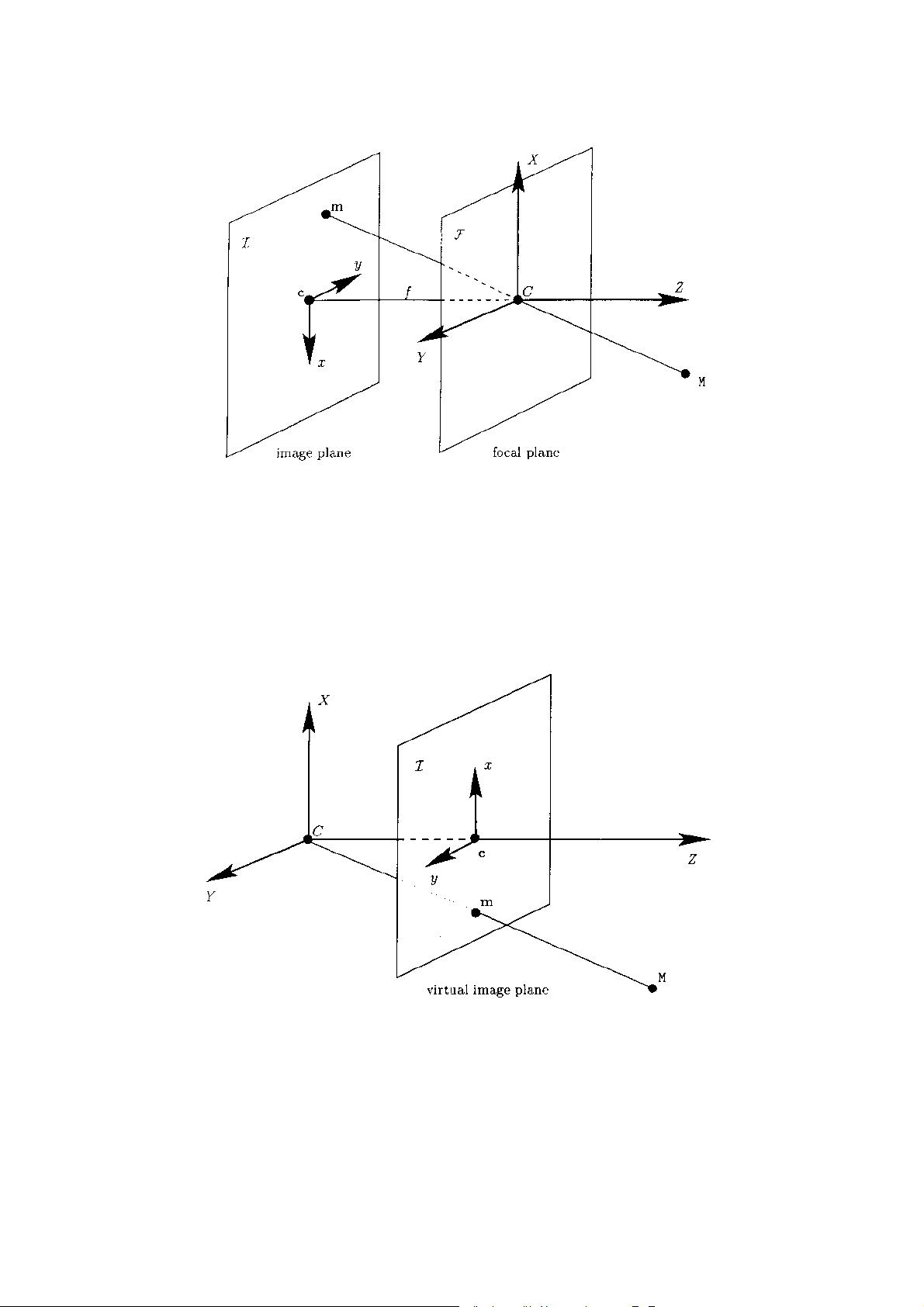
摄像机透视模型和外极线几何

### 摄像机透视模型和外极线几何 #### B.1 摄像机模型 ##### B.1.1 针孔模型和透视投影 针孔模型是一种简单的摄像机模型，用来模拟真实世界的摄像机如何将三维空间中的场景投影到二维的图像平面上。这种模型的核心在于透视投影，即远处的物体看起来比近处的小。 **针孔模型的几何关系：** - **定义坐标系：** - **摄像机坐标系**：原点位于焦心C，X、Y、Z轴分别由A、H'和V'决定，其中A指向光轴方向，而H'和V'与水平和垂直方向正交，形成右手直角坐标系。 - **图像坐标系**：原点位于光轴与图像平面的交点c（主点），两坐标轴与H'和V'平行且方向相反。 - **投影关系**：三维点\( (X_c, Y_c, Z_c)^T \)在图像平面上的投影坐标为\( (u, v)^T \)，具体投影公式为： \[ u = f\frac{X_c}{Z_c}, \quad v = f\frac{Y_c}{Z_c} \] 其中\( f \)为焦距，即焦心到图像平面的距离。 **透视投影的性质：** - 当物体距离焦心远远大于焦距时，可以使用虚拟图像平面来简化计算。此时，虚拟图像平面位于实际图像平面关于焦心对称的位置，虚拟平面上的坐标与三维点的摄像机坐标满足相同的投影关系。 ##### B.1.2 摄像机外参数 **定义**：摄像机外参数包括旋转矩阵\( R \)和位置向量\( t \)，用于描述摄像机相对于世界坐标系的位置和方向。 - **旋转矩阵\( R \)**：表示摄像机的方向。 - **位置向量\( t \)**：表示世界坐标系原点在摄像机坐标系中的坐标。 - **坐标转换公式**：\( M_c = RM + t \)，其中\( M_c \)为摄像机坐标系中的坐标，\( M \)为世界坐标系中的坐标。 ##### B.1.3 摄像机内参数和归一化摄像机 **问题描述**： - 图像坐标系与像素坐标系不完全一致，可能存在的差异包括：原点位置、单位长度不同、坐标轴不成直角等。 - 通过仿射变换处理这些问题。 **摄像机内参数**： - **焦距\( f \)**：焦心到图像平面的距离。 - **主点偏移**：图像坐标系的原点与像素坐标系原点之间的偏移量。 - **像素尺寸**：像素坐标系中每单位长度对应的物理尺寸。 - **坐标轴倾斜**：像素坐标系中坐标轴之间的夹角偏差。 **归一化摄像机**： - 通过归一化操作消除摄像机内参数的影响，使得所有摄像机都具有统一的参数标准，便于比较和分析。 - 归一化摄像机的坐标系通常设为主点为原点、单位像素大小、坐标轴相互垂直的标准坐标系。 #### B.2 透视投影的各种线性近似 透视投影在实际应用中往往需要简化处理。这里介绍几种常用的线性近似方法： ##### B.2.1 正投影（orthographic projection） 正投影忽略深度信息，假设所有物体都位于同一平面上，因此投影结果不会随距离而变化。 ##### B.2.2 弱透视（weak perspective） 弱透视是透视投影的一种近似方法，适用于距离摄像机较远的场景。它假设所有物体到摄像机的距离大致相等，从而简化投影计算。 ##### B.2.3 平行透视（para-perspective projection） 平行透视是介于正投影和透视投影之间的一种方法，适用于需要保留一定透视效果但又希望简化计算的情况。 ##### B.2.4 仿射摄像机 仿射摄像机是另一种近似方法，适用于摄像机移动范围有限或场景中没有显著深度变化的情形。它通过仿射变换来模拟摄像机的运动。 #### B.3 透视投影下的外极线几何 ##### B.3.1 外极线几何中的概念 外极线几何（Epipolar Geometry）是多视图几何学的一个核心概念，它描述了两个或多个摄像机之间以及它们所拍摄的图像之间的几何关系。关键概念包括： - **基本点（epipole）**：摄像机光轴与图像平面交点的投影。 - **外极线（epipolar line）**：通过基本点的一条直线，表示一个摄像机视图中点在另一个摄像机视图中的可能位置。 - **基础矩阵（Fundamental Matrix F）**：连接两个摄像机视图中对应点的线性关系。 - **基本矩阵（Essential Matrix E）**：仅考虑摄像机内参数已知的情况下的特殊基础矩阵。 ##### B.3.2 归一化坐标系中的外极线方程 在归一化坐标系中，外极线方程可以用更简单的形式表示。这有助于简化计算过程，并提高算法的效率。 ##### B.3.3 像素坐标系中的外极线方程 在外极线几何的实际应用中，通常需要将外极线方程从归一化坐标系转换到像素坐标系。这个过程中需要考虑摄像机的内参数，包括焦距、主点偏移等因素。 ##### B.3.4 投影矩阵下的外极线方程 投影矩阵\( P \)综合了摄像机内外参数的信息，通过投影矩阵可以方便地在不同摄像机视图之间建立联系。投影矩阵下的外极线方程能够更加准确地描述两视图之间的几何关系。 ##### B.3.5 基础矩阵和外极几何变换 基础矩阵\( F \)和基本矩阵\( E \)在外极线几何中起着核心作用。通过这些矩阵，可以实现从一个摄像机视图到另一个摄像机视图中对应点的精确匹配，这对于立体匹配、三维重建等问题至关重要。 摄像机透视模型和外极线几何是模式识别和计算机视觉领域的基础概念。理解这些原理对于开发高效的图像处理算法和实现可靠的视觉系统具有重要意义。