mean-shift算法概述

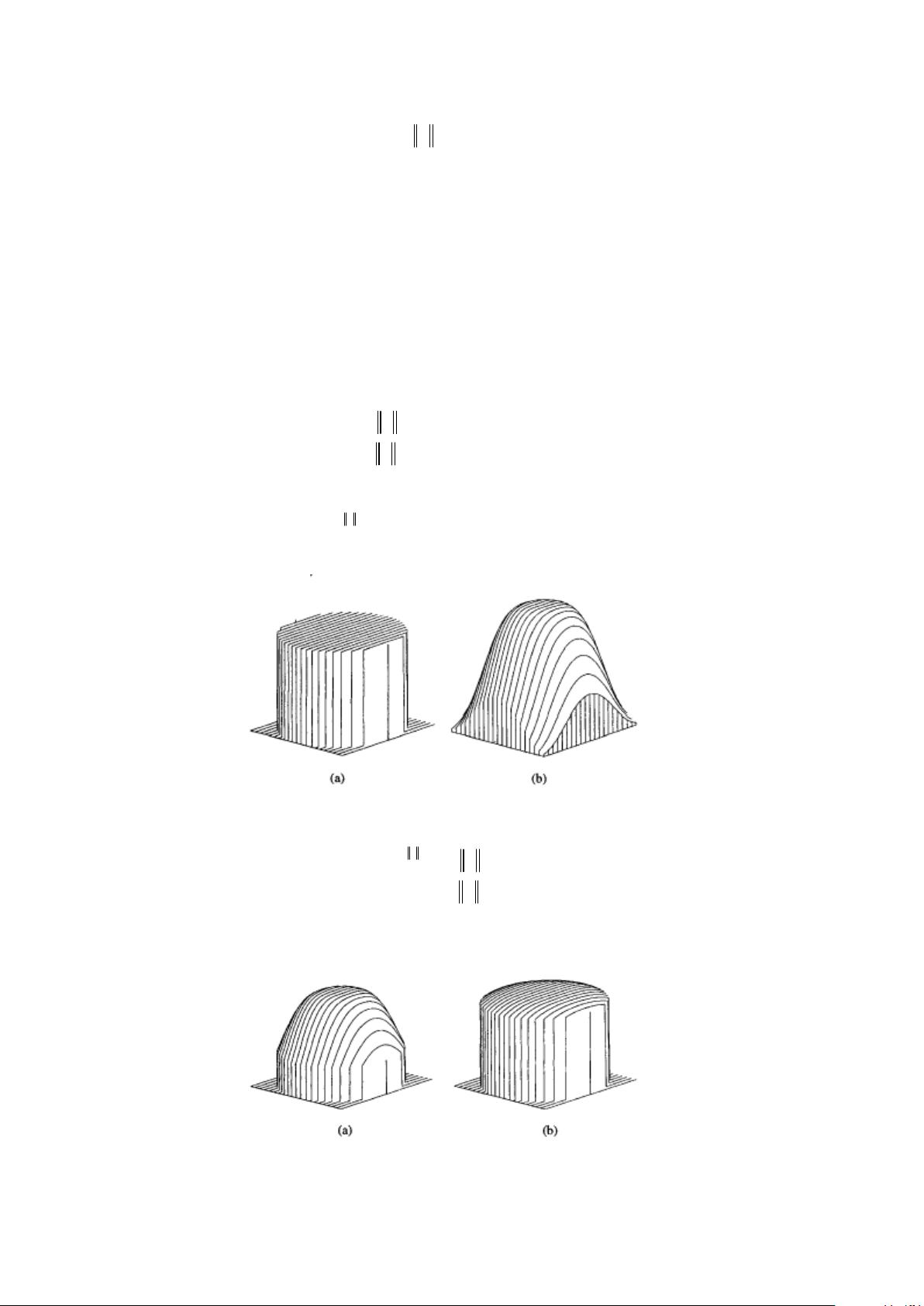
### Mean-Shift算法概述 #### 一、Mean-Shift算法的历史背景与发展 Mean-Shift算法是一种基于概率密度函数的方法，最初由Fukunaga等人在1975年的研究工作中提出，其最初的定义是一个简单的“偏移的均值向量”。随着时间的发展，这一概念逐渐演变成为一种迭代算法，其主要过程包括计算当前点的偏移均值，并将该点移动到计算出的新位置，这一过程重复进行直至满足特定的终止条件。 #### 二、Mean-Shift算法的关键发展 20年后，即1995年，Yizong Cheng发表的一篇重要论文对Mean-Shift算法进行了显著改进，主要包括： 1. **核函数的引入**：Yizong Cheng定义了一系列核函数，这些核函数可以根据样本点与参考点之间的距离赋予不同的权重，这意味着距离较近的点对均值偏移向量的影响更大。 2. **权重系数的设定**：除了核函数外，还引入了权重系数，允许对不同的样本点赋予不同的重要性，这极大地扩展了Mean-Shift算法的应用范围。 #### 三、Mean-Shift算法的应用领域 Yizong Cheng不仅提出了算法的改进，还指出了Mean-Shift算法可能的应用领域，并提供了实例。之后的研究者们进一步拓展了该算法的应用范围，包括但不限于图像处理领域： 1. **图像平滑**：利用Mean-Shift算法进行图像平滑处理，可以有效地去除图像中的噪声，同时保持边缘清晰。 2. **图像分割**：在图像分割任务中，Mean-Shift算法能够根据像素的颜色或纹理特性将其归类到不同的区域，从而实现高效的图像分割。 3. **物体实时跟踪**：Comaniciu等人将非刚体跟踪问题转化为Mean-Shift优化问题，实现了物体的实时跟踪。 #### 四、Mean-Shift算法的基本原理 给定一组数据点 \[ x_i, i = 1, \ldots, n \] 在多维空间 \[ \mathbb{R}^d \] 中，Mean-Shift向量的基本形式定义为： \[ M_h(x) = \frac{\sum_{x_i \in S_h(x)} (x_i - x)}{k} \] 其中， \[ S_h(x) = \left\{ y : \|y - x\|^2 \leq h^2 \right\} \] 是半径为 \[ h \] 的高维球区域，包含了距离 \[ x \] 小于等于 \[ h \] 的所有点；而 \[ k \] 是落入此区域内的样本点数量。 #### 五、扩展的Mean-Shift算法 为了更灵活地适应不同类型的数据分布，引入了核函数的概念。核函数 \[ K(\cdot) \] 可以定义为： \[ K(x) = k(\|x\|^2) \] 其中 \[ k(\cdot) \] 是满足特定条件的剖面函数。常用的核函数包括高斯核、Epanechnikov核等，这些核函数可以根据实际情况选择使用。 #### 六、算法的迭代过程与收敛性 Mean-Shift算法通过不断迭代计算当前点的偏移均值，逐步向概率密度的最大值移动，最终收敛到局部最大值。这意味着算法能够在数据集中找到潜在的模式或簇。 #### 七、结论与展望 Mean-Shift算法作为一种有效的模式寻找工具，在图像处理、计算机视觉等领域有着广泛的应用前景。随着研究的深入和技术的进步，预计未来Mean-Shift算法将在更多领域展现出其独特的优势，并为解决实际问题提供更加高效和准确的方法。