【swjtu】数据结构第4次作业.docx

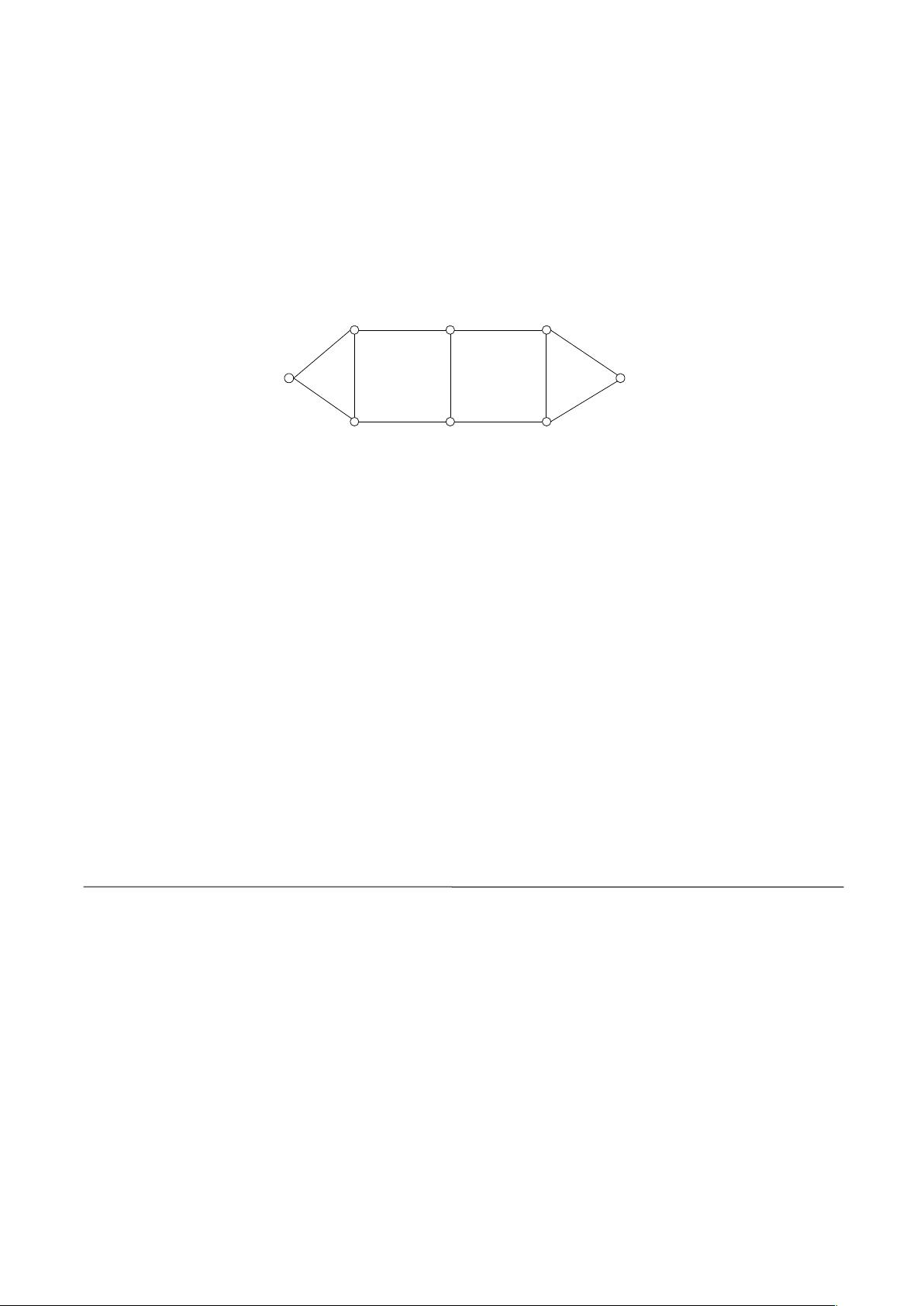
2. 写算法 (1) 二叉树的直径定义为从根结点至叶子的最大路径长度。编写算法，求二叉树(二叉链表)的直径。 (2) 已知二叉树(二叉链表)根结点指针bt，利用二叉树叶子结点的rchild指针域将所有叶子结点从左向右连接成一个单向链表。算法返回单向链表头结点指针(即最左边第1个叶子结点的地址)。 3. 上机题 (1) 用先序遍历法建立二叉树二叉链表存储结构(结点数据域类型为char，输入字符序列用字符'#'表示NULL)，实现中序线索化，并用非递归算法输出中序遍历结果的正序和逆序序列 1. 简答题 1. 已知某无向图如下图所示。画出该图的多重邻接表存储结构示意图。根据该存储结构，写出从顶点v0出发，深度和宽度优先遍历顶点访问次序。 2. 写算法 1. 写一个算法，判断无向图是否有环。算法提要：深度优先遍历过程中，访问某顶点后，该顶点的邻接点中有已访问的顶点且该已访问邻接点不是该顶点的上一级递归出发顶点(即存在回边)，则有环。 3. 上机题 1. 编程题: 建立无向图邻接表存储结构，输出深度和宽度优先遍历顶点访问次序。 2. 编程题：建立AOE网络存储结构，计算并输出ve[]和vl[]。 数据结构是计算机科学中的核心课程，它探讨了数据的有效组织和管理方式，以优化算法的效率。本作业涉及的主要知识点包括二叉树和图的处理。 1. **二叉树的直径**： - **定义**：二叉树的直径是指从根节点到任意两个叶子节点之间的最长路径长度。这个路径可能不经过根节点。 - **算法**：求解二叉树直径通常采用深度优先搜索(DFS)或广度优先搜索(BFS)。对于每个节点，分别计算以它为根的左子树和右子树的最大深度，然后取其中的最大值加上当前节点的高度，得到以该节点为根的子树的直径。比较所有节点的子树直径，取最大值即为整个二叉树的直径。 2. **连接叶子节点**： - **任务**：给定二叉树的根节点指针`bt`，利用叶子节点的`rchild`指针域，将所有叶子节点从左向右连接成一个单向链表。 - **实现**：可以使用深度优先搜索，每次到达叶子节点时，将其`rchild`指针连接到前一个叶子节点。初始时，最左边的叶子节点的`rchild`为空，后续叶子节点的`rchild`指向前一个叶子节点。 3. **先序遍历构建二叉树**： - **方法**：先序遍历顺序为根-左-右。输入字符序列，遇到'#'表示空节点。根据输入创建二叉链表存储结构，并实现中序线索化。 - **线索化**：在二叉链表中添加线索，以便非递归中序遍历。线索化过程涉及到修改指针，将`lchild`和`rchild`指针改为前驱和后继节点的指针。 4. **图的遍历**： - **深度优先搜索(DFS)**：从顶点v0出发，访问每个相邻的未访问顶点，记录访问顺序。在DFS过程中，如果发现已访问过的邻接点且它不是直接上级，说明存在环。 - **宽度优先搜索(BFS)**：同样从v0开始，按层次顺序访问所有顶点，BFS通常使用队列实现。 5. **判断无向图是否有环**： - **算法**：使用DFS，标记已访问过的节点。当访问一个节点时，检查其邻接点中是否有已访问过但不是直接上级的节点。若有，则存在环。 6. **邻接表存储结构**： - **构建**：对于无向图，邻接表是一个数组，每个元素对应图中的一个顶点，包含一个链表，链表中的每个节点表示与该顶点相邻的其他顶点。 - **遍历**：根据邻接表，可以很容易地进行深度优先和宽度优先遍历，输出访问次序。 7. **AOE网络**： - **存储结构**：AOE(Arc-Orientation Edge)网络用于表示活动-on-the-edge的项目网络图，通常用于项目计划和调度。 - **计算ve[]和vl[]**：ve[]是事件的最早开始时间，vl[]是事件的最迟结束时间。通过拓扑排序和松弛操作计算这些值，确保项目计划的可行性。 以上是对作业中涉及的二叉树和图相关知识的详细说明。理解并掌握这些概念和算法是理解和解决复杂问题的基础。