数字信号处理-基于巴特沃思模拟低通与数字频带变换的IIR高通数字滤波器设计

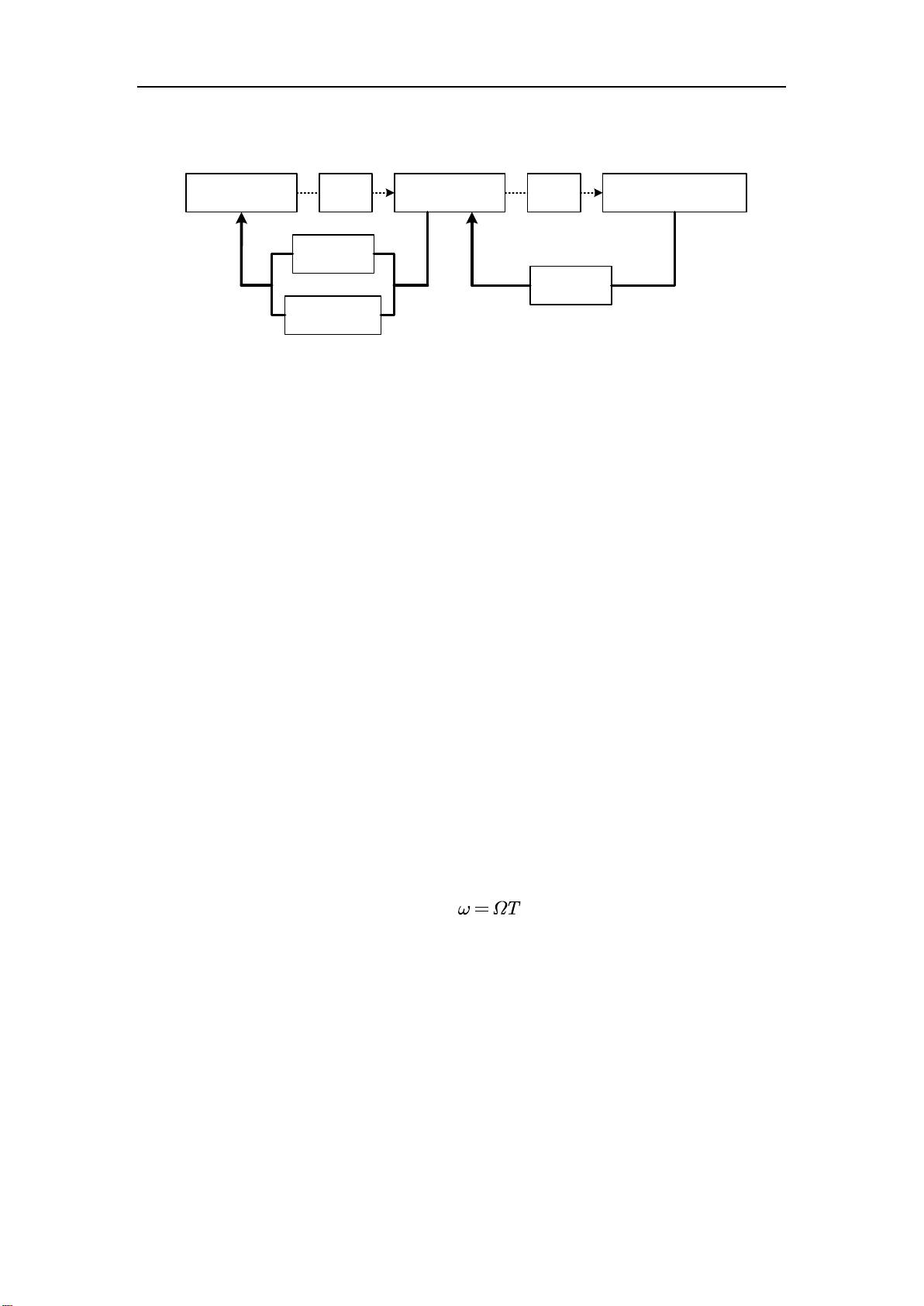
（1）五种模拟滤波器类型的比较 a) 巴特沃斯滤波器（Butterworth）：具有单调下降的幅频特性，过渡带最宽； b) 切比雪夫Ⅰ型滤波器（Chebyshev1）：在通带具有等波纹幅频特性，过渡带和阻带是单调下降的幅频特性； c) 切比雪夫Ⅱ型滤波器（Chebyshev2）：通道带幅频响应几乎与巴特沃斯滤波器相同，阻带是等波纹幅频特性； d) 椭圆滤波器（Ellipse）：过渡带最窄，通带和阻带均是等波纹幅频特性； e) 贝塞尔滤波器（Bessel）：在整个通带逼近线性相位特性，而其幅频特性的过渡带比其他四种滤波器宽得多。 （2）两种系统函数转换方法的比较 a) 双线性变换法 优点：频率变换关系是线性的，即 ，如果不存在频谱混叠现象，用这种方法设计得数字滤波器会很好地重现原模拟滤波器的频响特性。另外，数字滤波器的单位脉冲响应完全模仿模拟滤波器的单位冲激响应波形，时域特性逼近好。 缺点：会产生不同程度的频谱混叠失真，其适用于低通、带通滤波器的设计，不适用于高通、带阻滤波器的设计。 b) 脉冲响应不变法 优点：可由简单的代数公式 将 直接转换成 且不存在频谱混叠现象。 缺点： 在数字信号处理领域，设计和应用IIR（无限冲击响应）滤波器是至关重要的，尤其是在高通滤波器的设计中。本课题关注的是基于巴特沃思模拟低通滤波器转换到数字高通滤波器的过程。巴特沃思滤波器以其平缓的幅频响应和宽的过渡带而闻名，是许多滤波器设计的基础。它在电子工程、通信和音频处理等应用中被广泛使用。 设计数字滤波器时，通常会涉及两种主要的系统函数转换方法：双线性变换法和脉冲响应不变法。双线性变换法保留了频率变换的线性特性，这使得设计的数字滤波器能较好地复制模拟滤波器的频率响应，特别是在低通和带通滤波器的设计中。然而，这种变换可能导致频谱混叠失真，不适于高通和带阻滤波器。另一方面，脉冲响应不变法允许直接从模拟滤波器转换到数字滤波器，但可能产生频谱混叠，且转换过程简单明了。 在数字滤波器设计中，IIR高通滤波器的实现通常包括以下步骤：根据技术指标将数字高通滤波器的要求转换为模拟低通滤波器的参数。接着，设计一个巴特沃思模拟低通滤波器。然后，通过脉冲响应不变法或双线性变换法，结合适当的频带变换将模拟滤波器转换为数字滤波器。在本设计中，选择了数字频带变换的方法，即将数字高通滤波器设计为数字低通滤波器，然后进行预畸变校正和频率归一化。 在比较不同类型的模拟滤波器时，可以看到每种滤波器都有其独特的特性。切比雪夫Ⅰ型滤波器在通带内有等波纹幅频特性，而切比雪夫Ⅱ型滤波器在阻带有等波纹特性。椭圆滤波器则提供了最窄的过渡带，而贝塞尔滤波器以其接近线性相位的特性著称，但其过渡带较宽。 在实际应用中，滤波器的实现结构和参数字长都会对性能产生影响。例如，直接型和级联型结构会影响滤波器的幅频响应，而参数字长的选取将影响精度和稳定性。更长的字长可以提高精度，但也会增加计算复杂性和存储需求。 设计IIR高通数字滤波器是一个涉及理论知识、仿真分析和实际实现多个层面的综合过程。理解各种滤波器类型的特点以及选择合适的转换方法对于实现满足特定要求的滤波器至关重要。在设计过程中，需要考虑滤波器的性能、实现结构的复杂性以及计算资源的限制，通过不断的分析和优化来达到最佳设计效果。