模拟退火 Vehicle Routing Problem (VRP) using Simulated Annealing (SA) with Matlab
> Fore more information please visit: www.lzane.com/mo-ni-tui-huo-vehicle-routing-problem-vrp-using-simulated-annealing-sa-with-matlab
### Simulation
让我们来想一个特例,80座城市,分布在四个角上,仓库在正中间,总共有四辆车。那么路程最短的解很明显可以想象出是每辆车分别去访问一个角。matlab工程在文末附件部分给出,仿真结果如下:
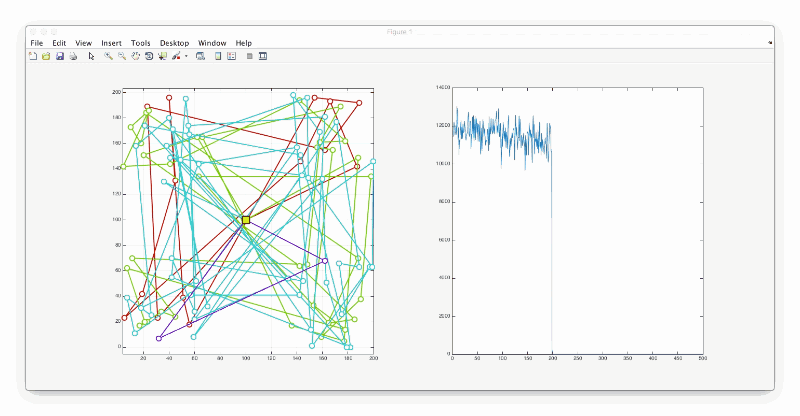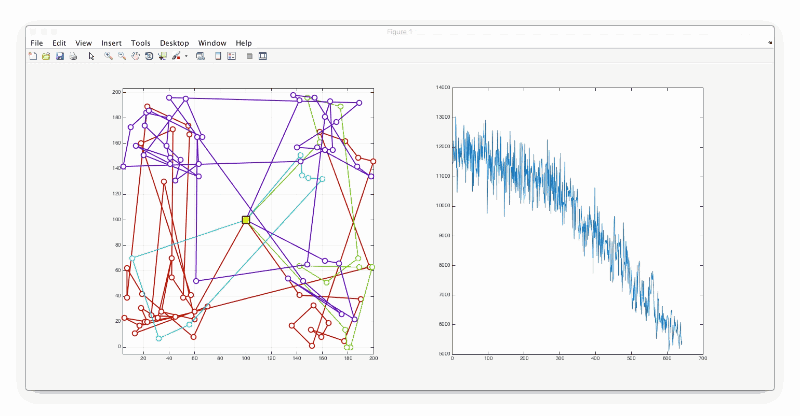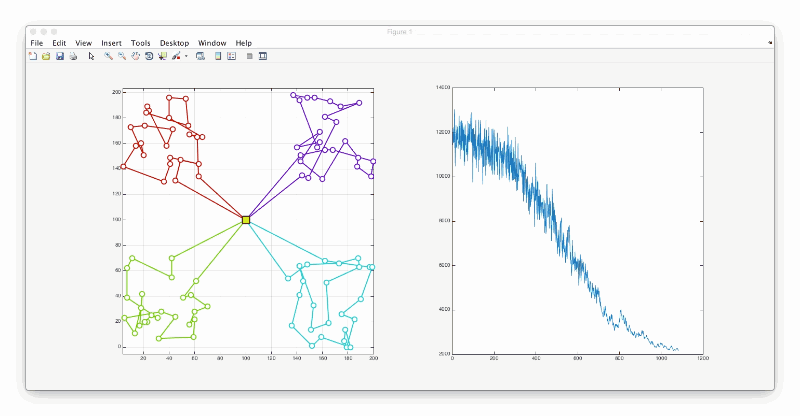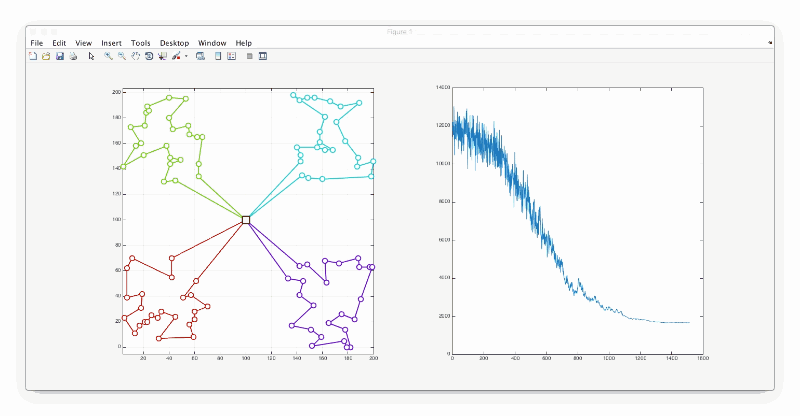
观察下图,可以看出一开始温度较高的时候,容易接受一个比自己差一点的解,从而跳出局部最优解,随着时间推移,温度降下来之后,就基本上不能再接受比自己再差的解了。
<img height="200px" src="https://qncdnssl.lzane.com/content/images/2016/05/Screen-Shot-2016-05-18-at-11-52-11-PM.png">
---------------
使用Matlab用模拟退火(SA)解决VRP问题。首先什么是VRP问题?
大家应该都知道旅行商问题(TSP,Traveling Salesman Problem),即求一个旅行家从一个仓库出发,通过沿途所有城市,再回到仓库所需要的最短路径。TSP问题中只有一个旅行商,那我们如何去解决有多个旅行商(车辆)同时送货的问题呢?
### VRP
这就引出了VRP问题,即在TSP问题的基础上,加上两个限定条件:
- 有多个旅行商(车辆)同时送货。
- 每个旅行商(车辆)能携带的货物量(capacity)。
也就是说,TSP问题是VRP问题的一个特例(不考虑capacity并且只有一辆车的情况)。
现在为了简化问题,我们先不考虑汽车容量,只考虑有多个旅行商(车辆)时我们应该如何解决这个问题。
下图是一个TSP问题的邻接矩阵 (D是仓库)
<img height="200px" src="https://qncdnssl.lzane.com/content/images/2016/05/Screen-Shot-2016-05-18-at-11-09-45-PM.png">
我们从[ABC]随机生成一个排列组合,然后再将D接到这个序列的两头即得出了一条路线。
<img height="200px" src="https://qncdnssl.lzane.com/content/images/2016/05/Screen-Shot-2016-05-18-at-11-12-42-PM.png">
现在考虑VRP问题,假设现在我们有两辆汽车,其实我们需要做的只是在原来的矩阵多加一行一列,然后把一辆车当成是城市,也可以理解成有多少辆车就有多少个仓库,但他们在地图上其实是一点,然后对[A B C D1]进行排列组合,即可得到:
<img height="200px" src="https://qncdnssl.lzane.com/content/images/2016/05/Screen-Shot-2016-05-18-at-11-14-47-PM.png">
然后把D2加到这个序列两头,就可以生成两条路线了(1. D-B-A-D 2.D-C-D)这样就把一个VRP问题装换成TSP问题了。
不过有两个方面要注意的:
- 生成的序列两头不能是D
- 不能有两个D连在一起
这两种情况都相当于少了一辆车
### 模拟退火 SA
首先看这张图,如果采用一般的贪心算法求最大值,那么当搜索到达A之后,就不会继续向前了,这就陷入了局部最优解。
<img height="200px" src="http://pic002.cnblogs.com/images/2010/63234/2010122016525713.png">
SA模拟退火算法就是解决这个问题的一个办法,模仿金属冶炼时的退火过程,以一定概率接受一个更差一点的解,从而跳出局部最优解。
具体算法的实现请参照文末参考文献,这里只是简单带过
- 假设温度比设置的最低温度高
- 假如生成的解比原来的解更优,则接受生成的较优解。
- 假如生成的解比原来的差,则计算 **P(dE)=exp(dE/(kT))**, 以一定的概率接受这个较差解,然后降温。
- 生成一个neighbor,重复整个过程。
生成neignbor的方法也多种多样,比如说:
- swap
- insert
- reverse
###### 参考文献:
- "Improvement heuristics for the Vehicle Routing Problem based on Simulated Annealing" —— Alex Van Breedam
###### matlab工程代码:
https://github.com/lzane/VRP-using-SA-with-Matlab
www.lzane.com
模拟退火算法求解VRP问题 车辆路径问题Matlab程序
需积分: 0 81 浏览量
更新于2024-08-04
收藏 19KB ZIP 举报
车辆路径问题(Vehicle Routing Problem,VRP)是一个经典的组合优化问题,涉及如何有效地分配车辆去访问多个客户点,并在满足约束条件的情况下最小化总行驶距离或成本。
假设有5个客户需求点和2辆车,每辆车的容量都足够大,可以服务所有客户。客户点之间的距离如下:
- 客户点1到客户点2的距离为5
- 客户点2到客户点3的距离为6
- 客户点3到客户点4的距离为7
- 客户点4到客户点5的距离为8
- 客户点5到客户点1的距离为9
- 车辆起始点(仓库)到每个客户点的距离分别为:仓库到客户点1为10,仓库到客户点2为12,仓库到客户点3为15,仓库到客户点4为6,仓库到客户点5为8。
随机生成两个初始解,例如:路径1: 客户点1 → 客户点2 → 客户点3 → 客户点4 → 客户点5,路径2: 仓库 → 客户点1 → 客户点2 → 客户点3 → 客户点4 → 客户点5。计算总距离:路径1为26,路径2为42。
在每次迭代中,对当前解进行扰动产生新解。扰动可以通过交换、插入或反转操作实现。
qq_50150617
- 粉丝: 12
- 资源: 13
最新资源
- 微信小程序源码-停车场微信小程序的设计与实现-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-网上商城-服务端-毕业设计源码-期末大作业.zip
- 动态0-1背包问题中的Q-learning算法实现及应用
- 微信小程序源码-网上商城设计-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-网上商城-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-网上商城设计-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序电影订票系统-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序电影订票系统-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序考试系统-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序考试系统-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序跑腿-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-微信小程序跑腿-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-小区租拼车管理信息系统-微信端-毕业设计源码-期末大作业.zip
- 微信小程序源码-消防隐患在线举报系统开发-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-小区租拼车管理信息系统-服务端-毕业设计源码-期末大作业.zip
- 微信小程序源码-校车购票微信小程序-微信端-毕业设计源码-期末大作业.zip














