没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论
八年级[丄]数学期末《全等三角形》《轴对称》复
习提优题【大海之音组卷】
一.选择题(共 4 小题)
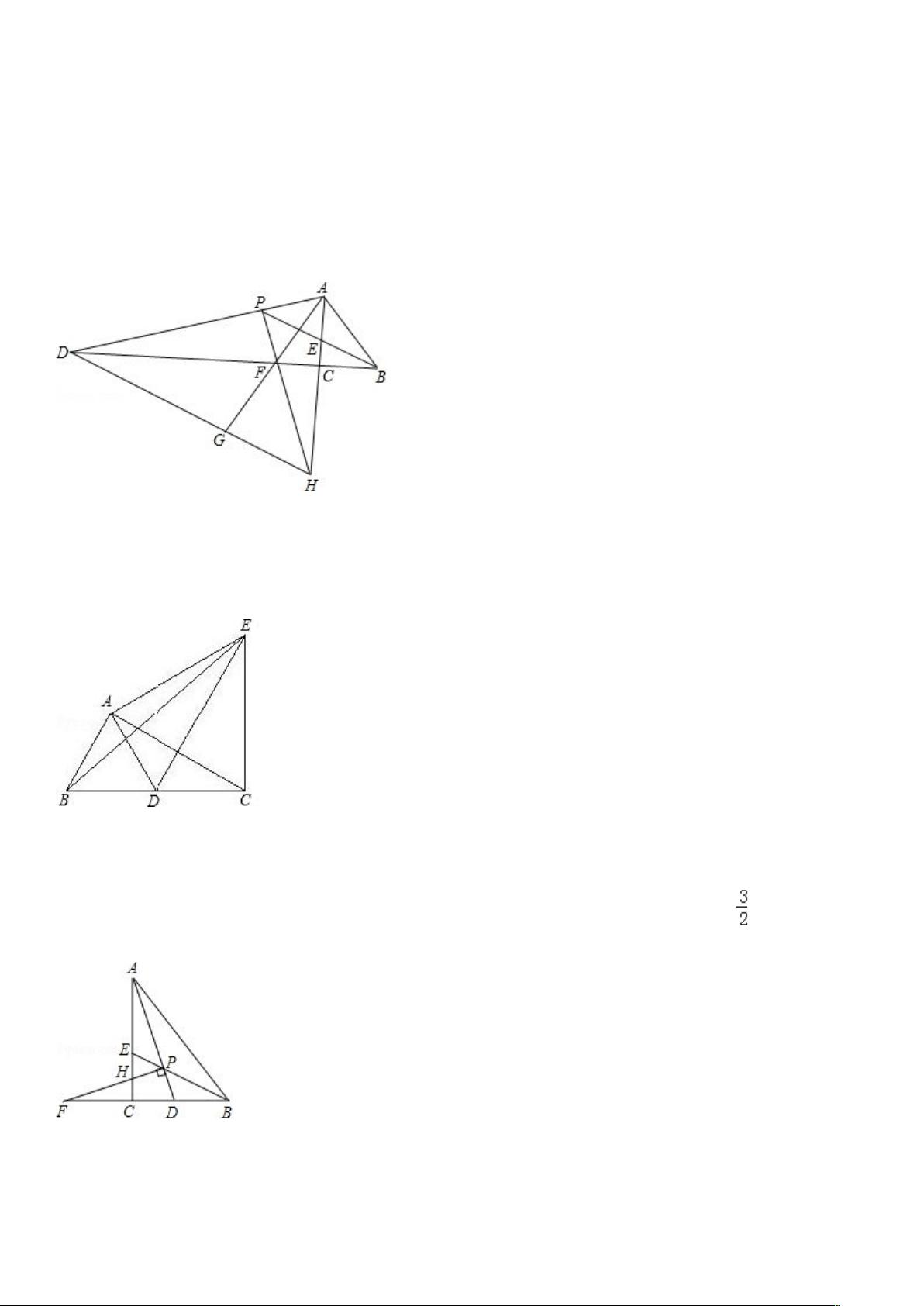
1.如图,Rt ACB△ 中,∠ACB=90°,∠ABC 的角平分线 BE 和∠BAC 的外角平分线 AD 相交于点 P,分别交 AC 和
BC 的延长线于 E,D.过 P 作 PF AD⊥ 交 AC 的延长线于点 H,交 BC 的延长线于点 F,连接 AF 交 DH 于点 G.则
下列结论:①∠APB=45°;② PF=PA;③ BD AH=AB﹣ ;④ DG=AP+GH.其中正确的是( )
A.
①②③
B.
①②④
C.
②③④
D.
①②③④
2.如图,将 30°的直角三角尺 ABC 绕直角顶点 A 逆时针旋转到 ADE 的位置,使 B 点的对应点 D 落在 BC 边上,
连接 EB、EC,则下列结论:①∠DAC= DCA∠ ;② ED 为 AC 的垂直平分线;③ EB 平分∠AED;④ ED=2AB.其
中正确的是( )
A.
①②③
B.
①②④
C.
②③④
D.
①②③④
3.如图,Rt ACB△ 中,∠ACB=90°,△ABC 的角平分线 AD、BE 相交于点 P,过 P 作 PF AD⊥ 交 BC 的延长线于
点 F,交 AC 于点 H,则下列结论:①∠APB=135°;② PF=PA;③ AH+BD=AB;④ S
四边形
ABDE
= S
ABP△
,其中正确
的是( )
A.
①③
B.
①②④
C.
①②③
D.
②③
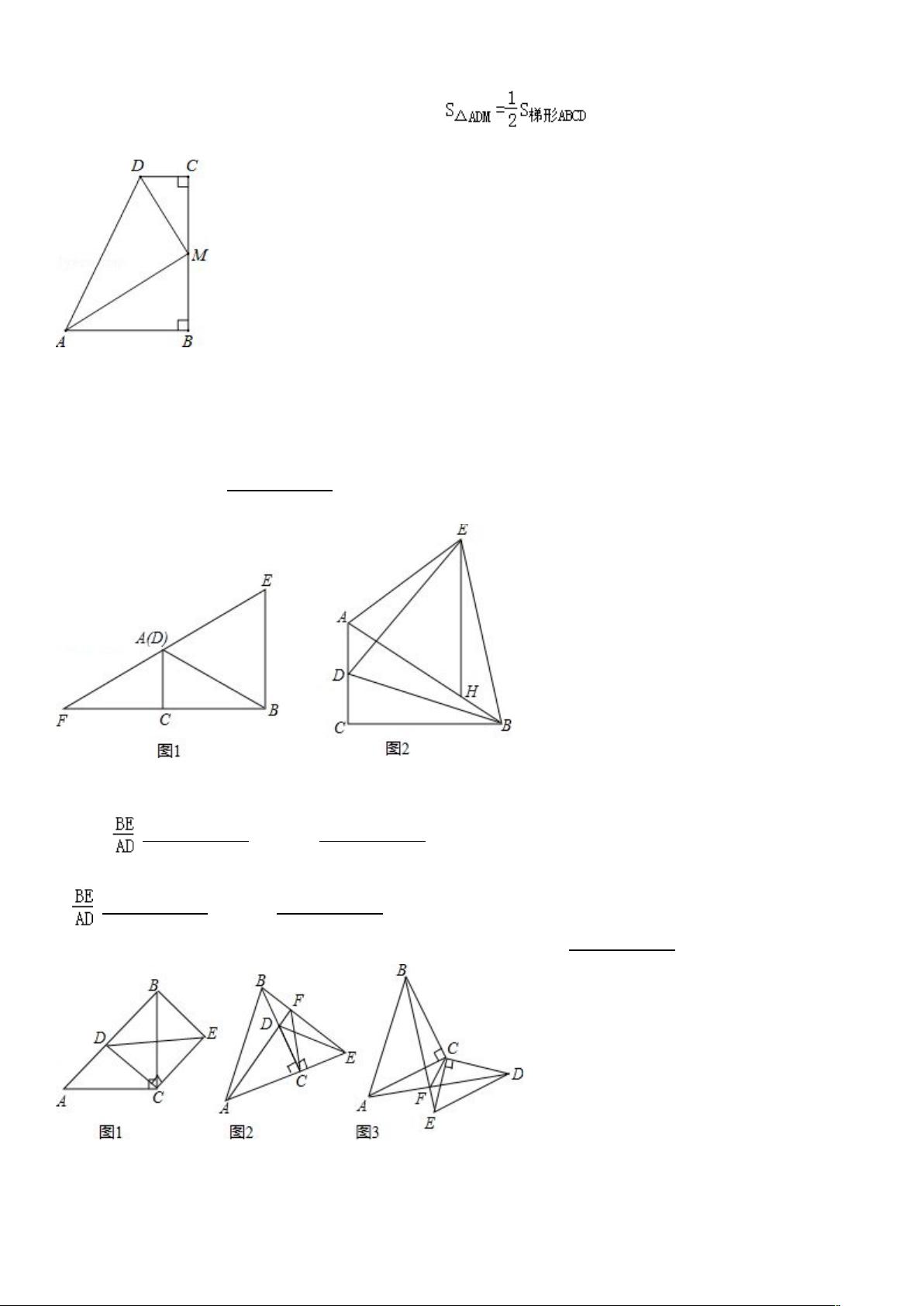
4.如图,在四边形 ABCD 中,∠B= C=90°∠ ,∠DAB 与∠ADC 的平分线相交于 BC 边上的 M 点,则下列结论:①
∠AMD=90°;② M 为 BC 的中点;③ AB+CD=AD;④ ;⑤ M 到 AD 的距离等于 BC 的一半;
其中正确的有( )
A.2 个 B.3 个 C.4 个 D.5 个
二.解答题(共 8 小题)
5.如图 1,在 Rt ACB△ 中,∠ACB=90°,∠ABC=30°AC=1 点 D 为 AC 上一动点,连接 BD,以 BD 为边作等边
△BDE,EA 的延长线交 BC 的延长线于 F,设 CD=n,
(1)当 n=1 时,则 AF= _________ ;
(2)当 0<n<1 时,如图 2,在 BA 上截取 BH=AD,连接 EH,求证:△AEH 为等边三角形.
6.两个等腰直角△ABC 和等腰直角△DCE 如图 1 摆放,其中 D 点在 AB 上,连接 BE.
(1)则 = _________ ,∠CBE= _________ 度;
(2)当把△DEF 绕点 C 旋转到如图 2 所示的位置时(D 点在 BC 上),连接 AD 并延长交 BE 于点 F,连接 FC,
则 = _________ ,∠CFE= _________ 度;
(3)把△DEC 绕点 C 旋转到如图 3 所示的位置时,请求出∠CFE 的度数 _________ .
7.已知△ABC 为边长为 10 的等边三角形,D 是 BC 边上一动点:
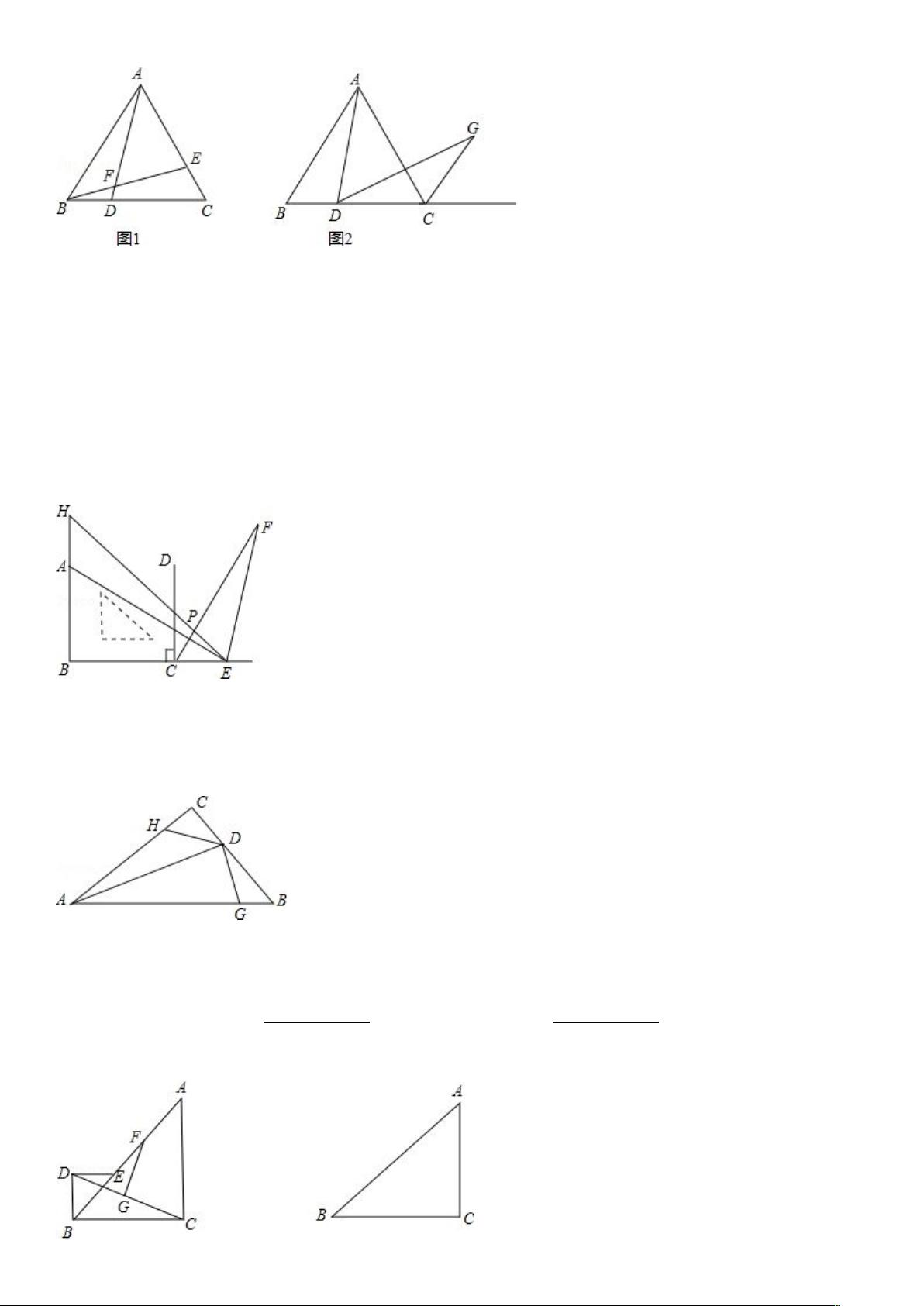
① 如图 1,点 E 在 AC 上,且 BD=CE,BE 交 AD 于 F,当 D 点滑动时,∠AFE 的大小是否变化?若不变,请求出
其度数.
② 如图 2,过点 D 作∠ADG=60°与∠ACB 的外角平分线交于 G,当点 D 在 BC 上滑动时,有下列两个结论:
① DC+CG 的值为定值;② DG CD﹣ 的值为定值.其中有且只有一个是正确的,请你选择正确的结论加以证明并
求出其值.
8.如图,点 A、C 分别在一个含 45°的直角三角板 HBE 的两条直角边 BH 和 BE 上,且 BA=BC,过点 C 作 BE 的
垂线 CD,过 E 点作 EF 上 AE 交∠DCE 的角平分线于 F 点,交 HE 于 P.
(1)试判断△PCE 的形状,并请说明理由;
(2)若∠HAE=120°,AB=3,求 EF 的长.
9.如图,AD 是△ABC 的角平分线,H,G 分别在 AC,AB 上,且 HD=BD.
(1)求证:∠B 与∠AHD 互补;
(2)若∠B+2 DGA=180°∠ ,请探究线段 AG 与线段 AH、HD 之间满足的等量关系,并加以证明.
10.如图,在等腰 Rt ABC△ 与等腰 Rt DBE△ 中,∠BDE= ACB=90°∠ ,且 BE 在 AB 边上,取 AE 的中点 F,CD 的
中点 G,连接 GF.
(1)FG 与 DC 的位置关系是 _________ ,FG 与 DC 的数量关系是 _________ ;
(2)若将△BDE 绕 B 点逆时针旋转 180°,其它条件不变,请完成下图,并判断(1)中的结论是否仍然成立?请
证明你的结论.
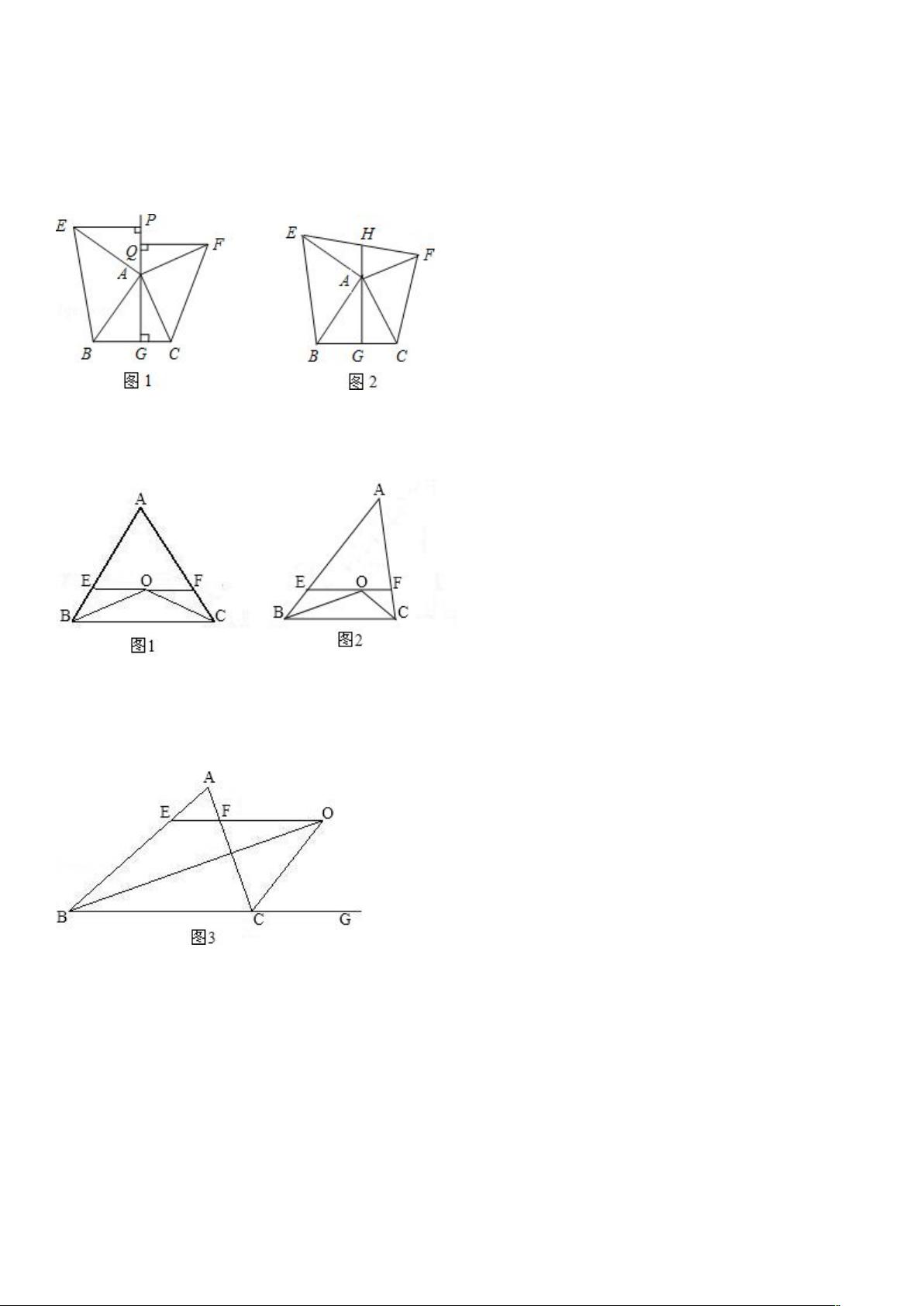
11.如图 1,△ABC 中,AG BC⊥ 于点 G,以 A 为直角顶点,分别以 AB、AC 为直角边,向△ABC 外作等腰
Rt ABE△ 和等腰 Rt ACF△ ,过点 E、F 作射线 GA 的垂线,垂足分别为 P、Q.
(1)试探究 EP 与 FQ 之间的数量关系,并证明你的结论.
(2)若连接 EF 交 GA 的延长线于 H,由(1)中的结论你能判断并证明 EH 与 FH 的大小关系吗?
(3)图 2 中的△ABC 与△AEF 的面积相等吗?(不用证明)
12.已知如图 1:△ABC 中,AB=AC,∠B、∠C 的平分线相交于点 O,过点 O 作 EF BC∥ 交 AB、AC 于 E、F.
① 图中有几个等腰三角形?请说明 EF 与 BE、CF 间有怎样的关系.
② 若 AB≠AC,其他条件不变,如图 2,图中还有等腰三角形吗?如果有,请分别指出它们.另第①问中 EF 与
BE、CF 间的关系还存在吗?
③ 若△ABC 中,∠B 的平分线与三角形外角∠ACD 的平分线 CO 交于 O,过 O 点作 OE BC∥ 交 AB 于 E,交 AC 于
F.如图 3,这时图中还有哪几个等腰三角形?EF 与 BE、CF 间的关系如何?为什么?
剩余19页未读,继续阅读
资源评论

CSGOGOTO
- 粉丝: 38
- 资源: 27万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功

