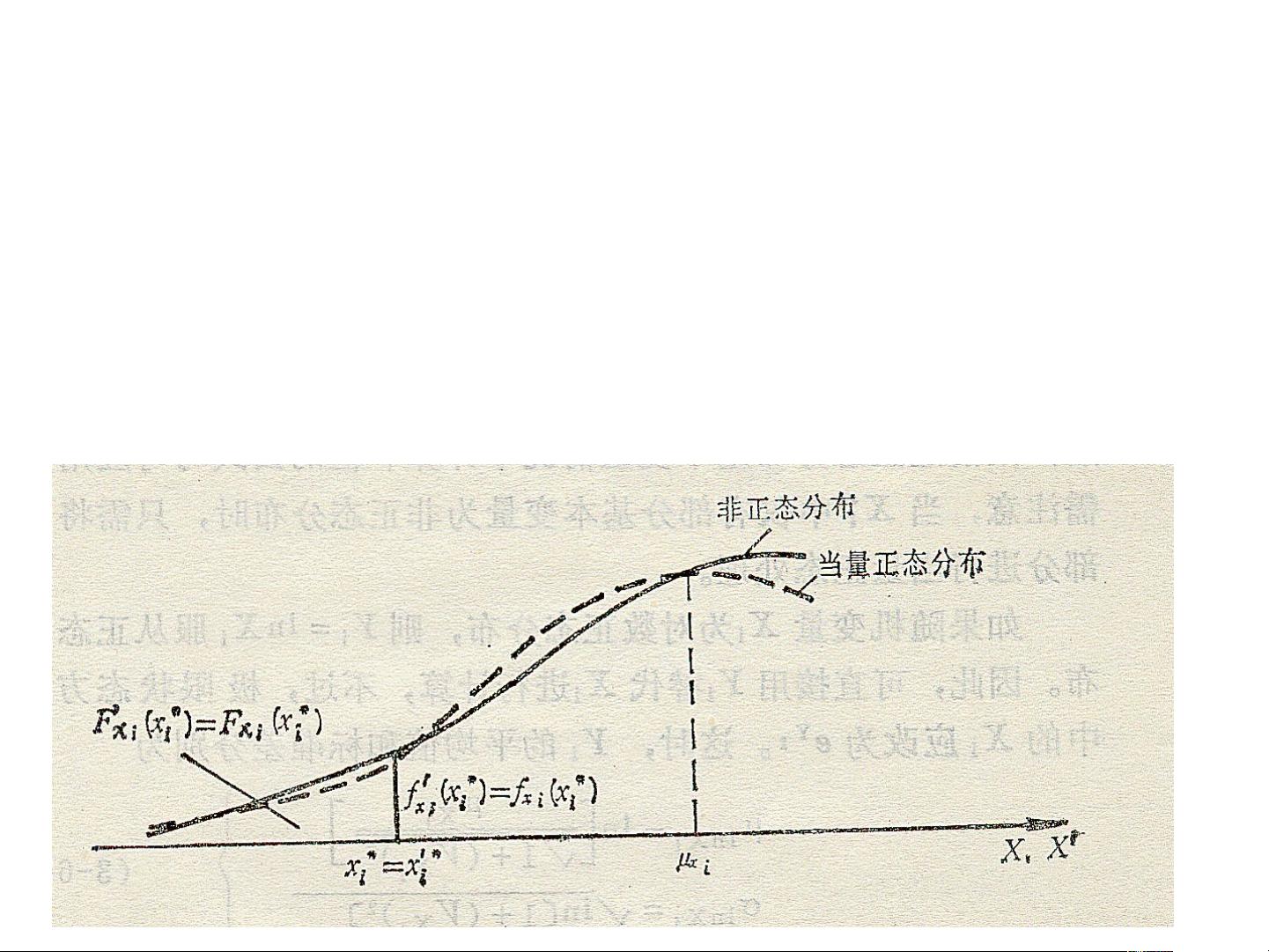
工程结构可靠度分析中，非正态分布的随机变量转换为正态分布是常见的处理方法，这是因为正态分布具有很多方便的性质，如对称性和中心极限定理，使得计算和分析更为简单。非正态分布转为正态分布的过程称为当量正态化。
当量正态化的条件有两个：
1. 在设计验算点P*处，非正态变量Xi与当量正态变量Xi'的概率分布函数值相等，即它们在尾部区域的面积相同。
2. 在设计验算点P*处，非正态变量Xi与当量正态变量Xi'的概率密度函数值也相等，意味着它们在该点的密度相同。
对于极值I型分布的随机变量Xi，转换成当量正态随机变量的平均值μ_Xi'和标准差σ_Xi'可以通过以下方式得到：
1. 使用条件①，通过比较两个变量在设计验算点P*处的概率分布函数，可以解出μ_Xi'。
2. 利用条件②，通过比较概率密度函数，可以解出σ_Xi'。
具体公式如下：
- 设计验算点P*处的概率分布函数相等：
\( F_{Xi}(x_i^*) = F_{Xi'}(x_i'^*) \)
- 设计验算点P*处的概率密度函数相等：
\( f_{Xi}(x_i^*) = f_{Xi'}(x_i'^*) \)
通过这些条件，我们可以求解出非正态随机变量Xi对应的当量正态随机变量Xi'的平均值μ_Xi'和标准差σ_Xi'。对于对数正态分布的随机变量，可以通过类似的方式进行转换，将对数正态分布的变量转换为对数正态的当量正态分布，然后进一步转换为标准正态分布。
对于非正态随机变量的处理，关键在于找到一个等价的正态分布，使得其在特定点的统计特性与原非正态分布相同。这样转换后，所有变量都成为正态分布，便于利用正态分布的性质进行计算和分析。
在实际工程应用中，如果结构极限状态函数包含了多个正态或非正态基本变量，可以采用迭代法来计算设计验算点P*和相关的统计参数。确定每个基本变量的概率分布类型和统计参数，然后进行当量正态化，最后通过迭代计算确定设计验算点的坐标值。
总结来说，工程结构可靠度分析中非正态分布转为正态分布的方法是一种常用的技术，它允许我们利用正态分布的便利性进行计算。通过满足特定的条件，我们可以将非正态分布的基本变量转换为正态分布，从而使整个分析过程更为简便。对于包含多种分布类型的变量，迭代法提供了一种有效的处理途径。
VIP享7折，此内容立减5.97元 
