离散数学的应用
Chan_Keyword
1 离散数学简介
离散数学(Discrete mathematics)是研究离散量的结构及其相互关系的数学
学科,是现代数学的一个重要分支。离散的含义是指不同的连接在一起的元素,
主要是研究基于离散量的结构和相互间的关系,其对象一般是有限个或可数个元
素。离散数学也叫组合数学,广义的组合数学就是离散数学,总之,组合数学是
一门研究离散对象的科学。随着计算机科学的日益发展,组合数学的重要性也日
渐凸显,因为计算机科学的核心内容是使用算法处理离散数据。狭义的组合数学
主要研究满足一定条件的组态(也称组合模型)的存在、计数以及构造等方面的
问题。 组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化(最
佳组合)等。
离散数学内容主要分为四大部分,分别是数理逻辑、集合论、代数结构和图
论。每个阶段内容都有深浅,在本科教学过程中,一般都讲解各部分的基础知识,
按各部分内容深浅由如下划分:
数理逻辑
命题逻辑、谓
词逻辑和推理
理论等
逻辑运算、位
运算
形式逻辑、智
能算法
搜索引
擎、硬件设计
集合论
集合、关系和
函数等
容斥、序列 运筹、密码 最优调度、软
件测试、公钥
代数结构
代数、半群、
群、环、域等
置换群、李群
近世代数
加密算法
图论
图、路径、回
路、树等
匹配、着色、
支撑、覆盖
图论应用 指令优化、路
径寻优
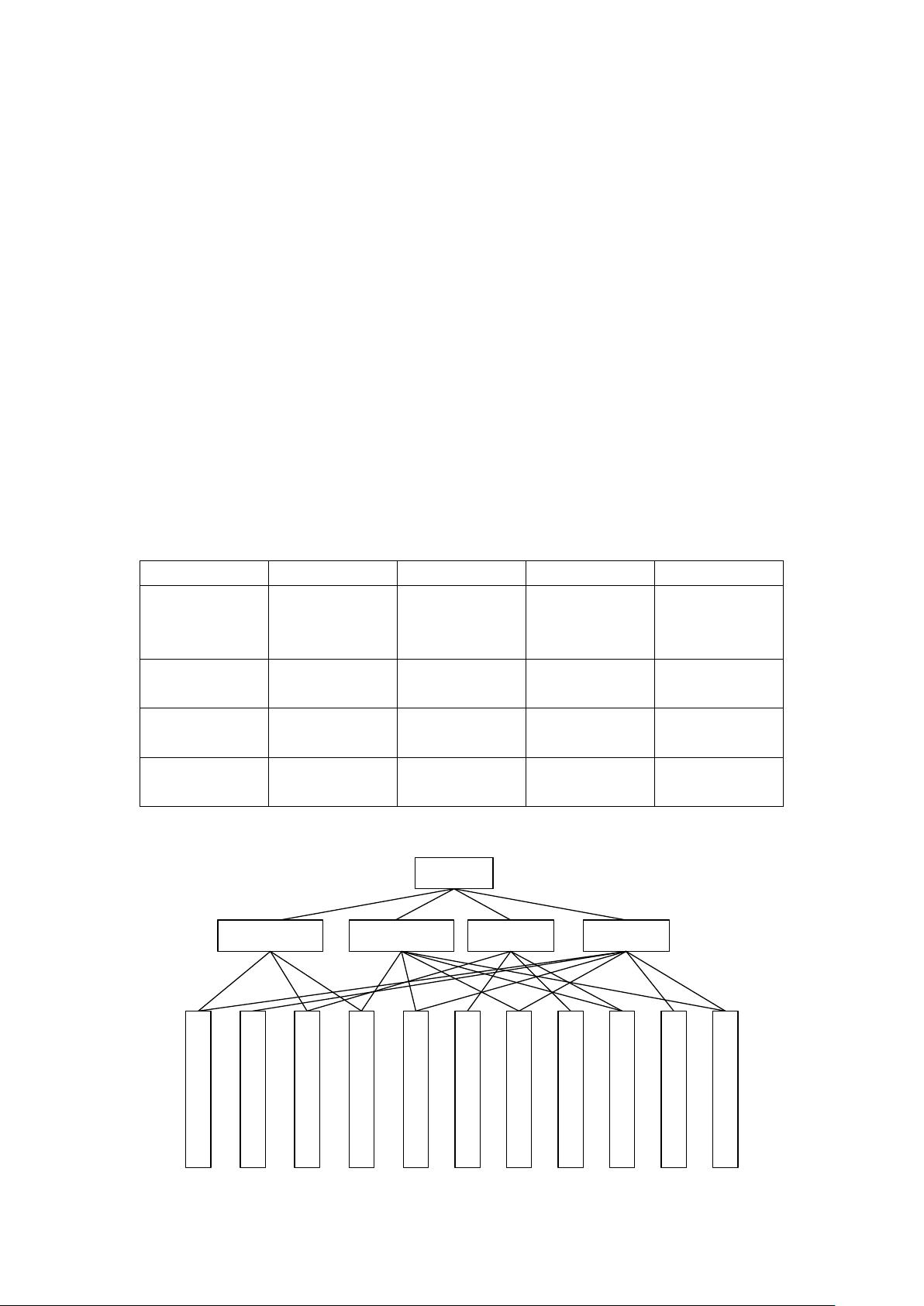
离散数学的知识内容及应用领域可用图 1.1 来概括。
离散数学离散数学
数理逻辑 集合与关系 代数系统 图论
网
络
协
议
分
析
网
络
安
全
计
算
机
组
成
与
结
构
数
据
库
原
理
编
译
原
理
现
代
密
码
学
数
据
结
构
软
件
工
程
信
息
论
与
编
码
数
字
水
印
隐
写
与
隐
写
分
析
图 1.1 离散数学各部分的应用
评论0
最新资源