数据结构赫夫曼树及其应用PPT学习教案.pptx

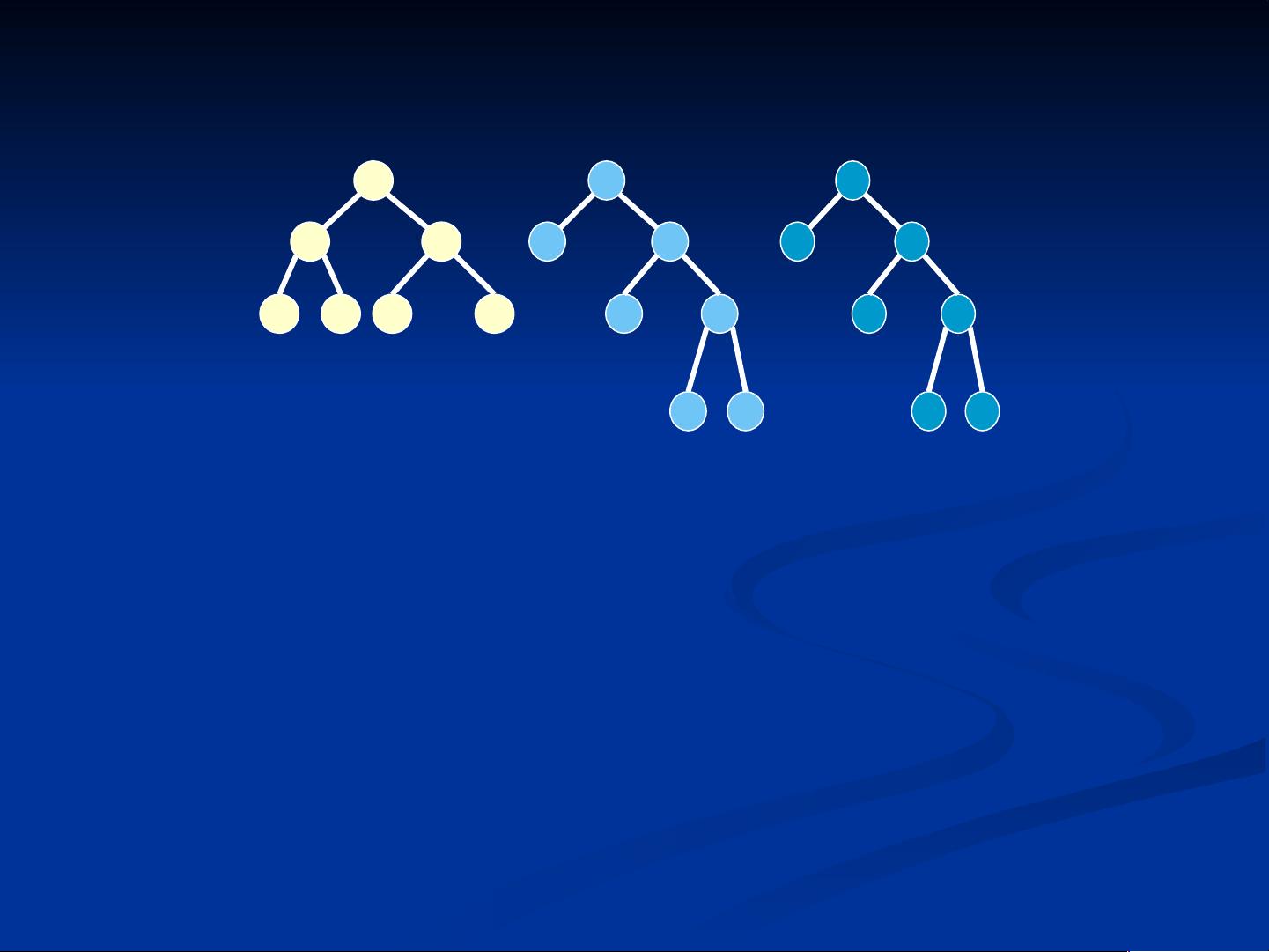
数据结构中的赫夫曼树（Huffman Tree），也被称为最优二叉树，是一种在特定应用场景下，能够优化路径长度的二叉树结构。赫夫曼树的构建是基于带权路径长度（Weighted Path Length, WPL）的概念，即从树的根节点到某个节点的路径长度与该节点权重的乘积。在数据处理和通信领域，赫夫曼树有广泛的应用，如压缩数据和提高传输效率。 构建赫夫曼树的过程通常包括以下步骤： 1. 针对给定的n个带权节点，创建n棵二叉树，每棵树只有一个带权重的根节点，左右子树为空。 2. 选取权值最小的两棵树，合并它们成为新的二叉树，新树的根节点权重为两棵子树的权重之和，将新树放入集合中。 3. 重复步骤2，每次从集合中移除两棵权值最小的树并生成新的树，直到集合中只剩下一棵树，这棵树就是赫夫曼树。 赫夫曼树的特性决定了它具有最小的带权路径长度。例如，在给定的四个叶子节点a、b、c、d，分别带有权值9、4、5、2的情况下，通过赫夫曼树的构建方法，可以找到WPL最小的二叉树结构，以达到优化路径的目的。 赫夫曼树在实际应用中，例如在判定问题中，可以提供最佳的决策算法。例如，对于学生百分成绩的分级问题，通过构建合适的赫夫曼树，可以减少判断成绩等级所需的比较次数。在成绩分布不均匀的情况下，利用赫夫曼树可以显著降低比较的复杂度，比如在处理10000个数据时，从原本的31500次比较降低到22000次。 此外，赫夫曼树在数据编码，特别是二进制编码方面也至关重要。在通信中，通过采用不等长的赫夫曼编码，可以为出现频率高的字符分配较短的编码，而频率低的字符则分配较长的编码，以此实现电文的高效压缩。关键在于保证编码的无前缀性，即任何字符的编码都不是其他字符编码的前缀，以确保正确解码。例如，给定字符集{A, B, C, D}，通过赫夫曼编码，可以将电文长度从14位缩短到9位，有效地节省了传输时间和资源。 赫夫曼树是一种用于优化带权重路径长度的二叉树结构，广泛应用于数据压缩、编码优化以及决策算法等领域，它的构造过程和应用特点体现了数据结构在实际问题中的智能解决方案。