自动控制系统原理 自动控制技术及其应用 第5章 频率响应法4 共39页.pptx

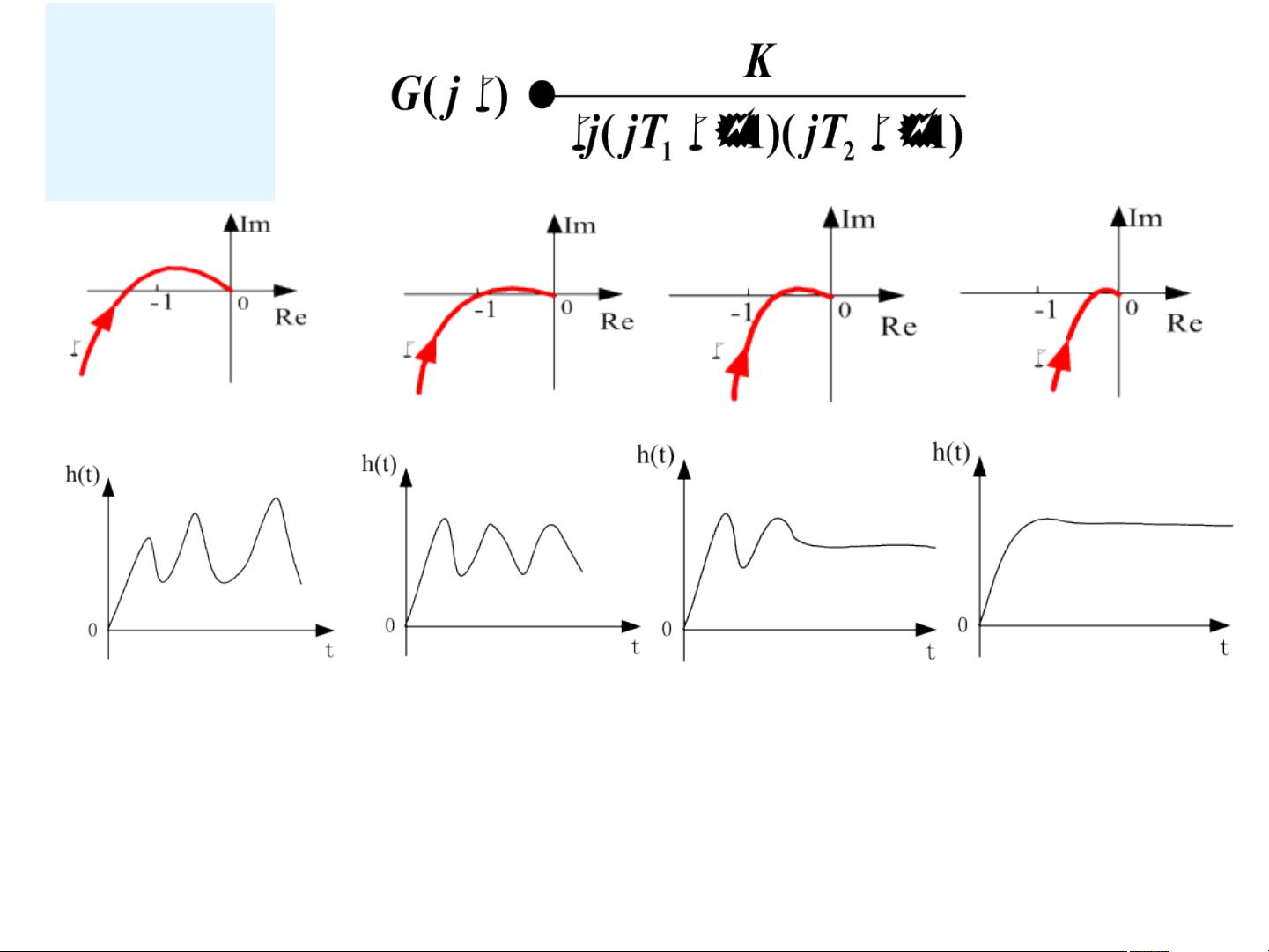
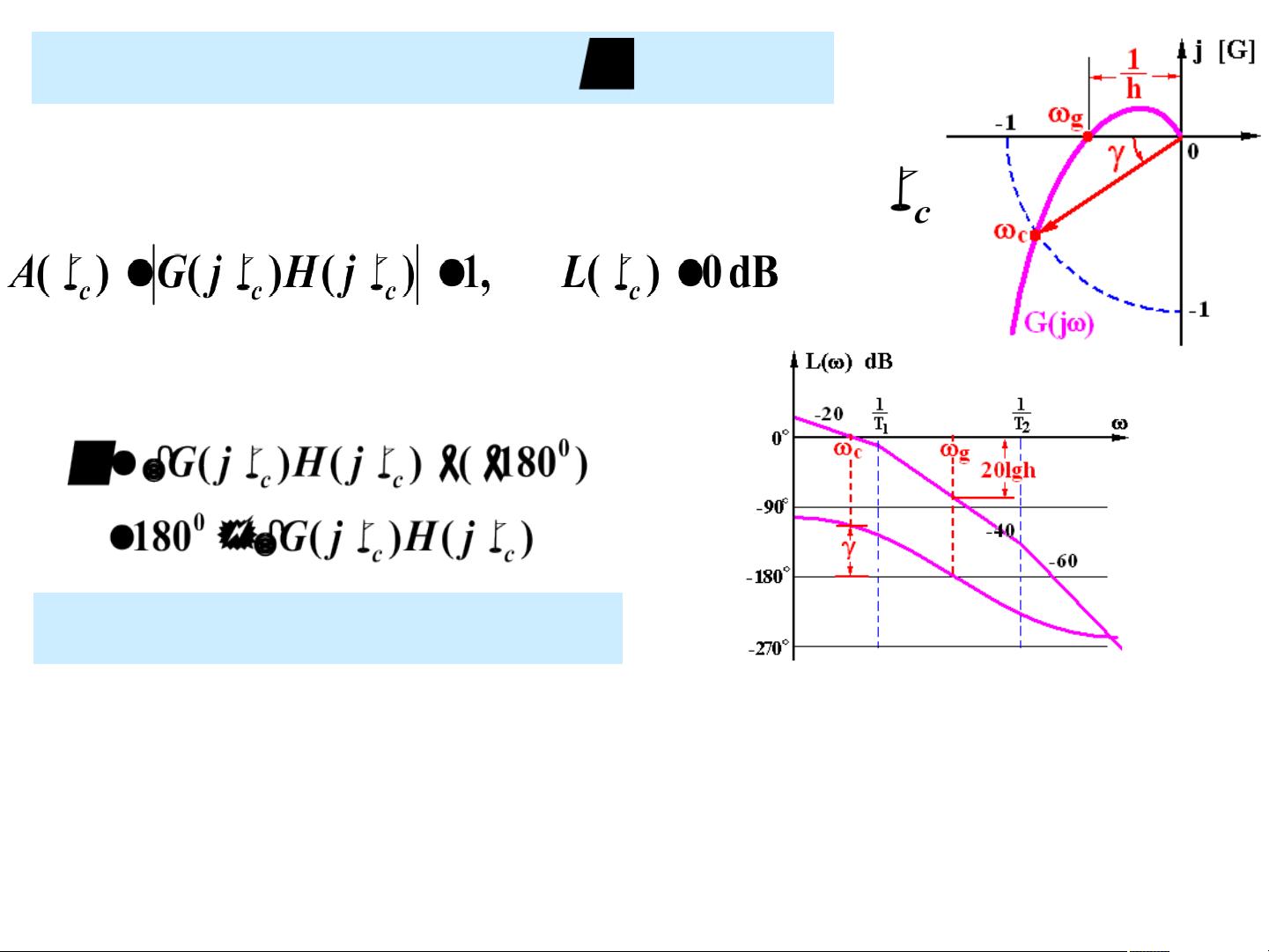
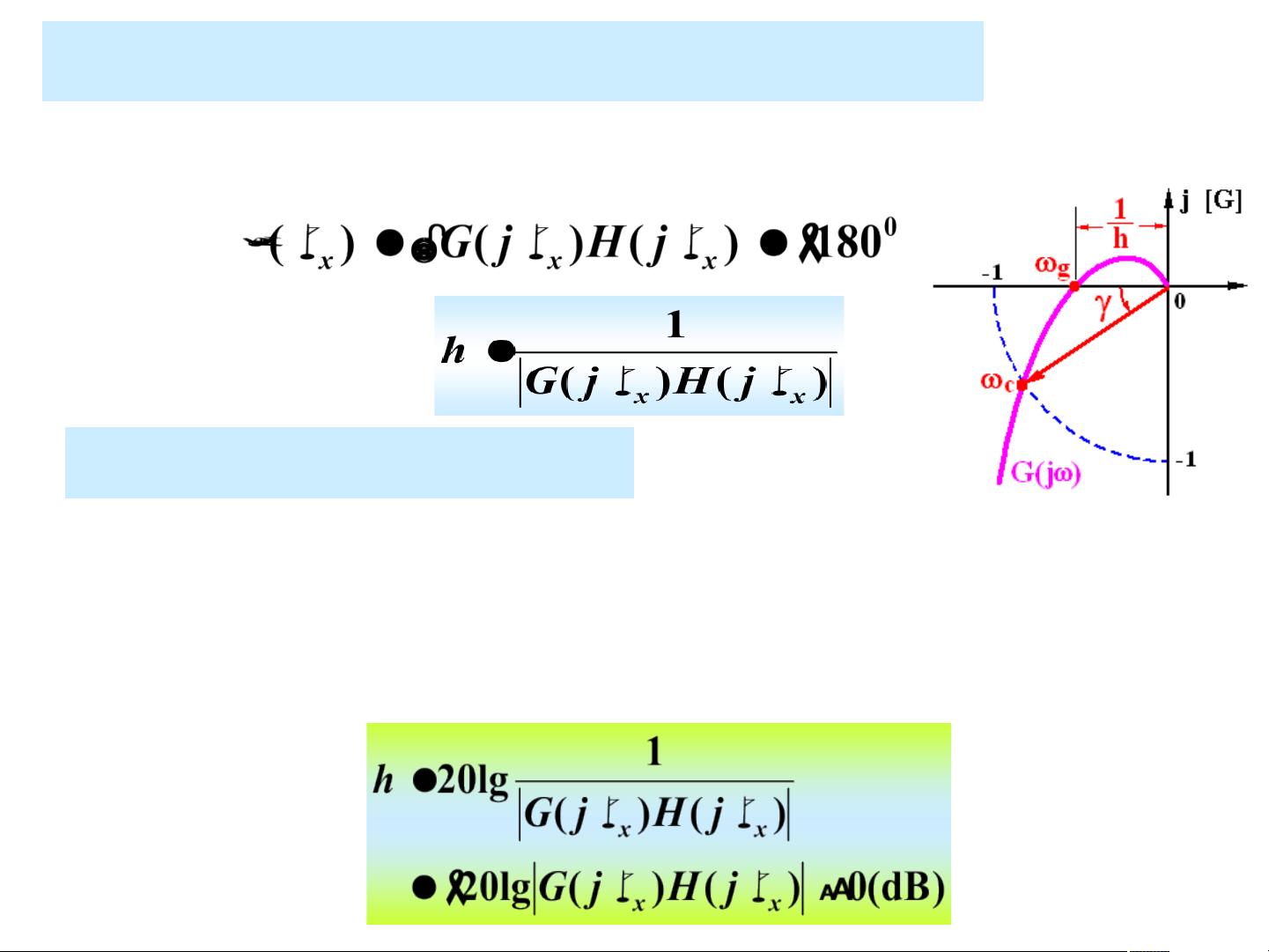
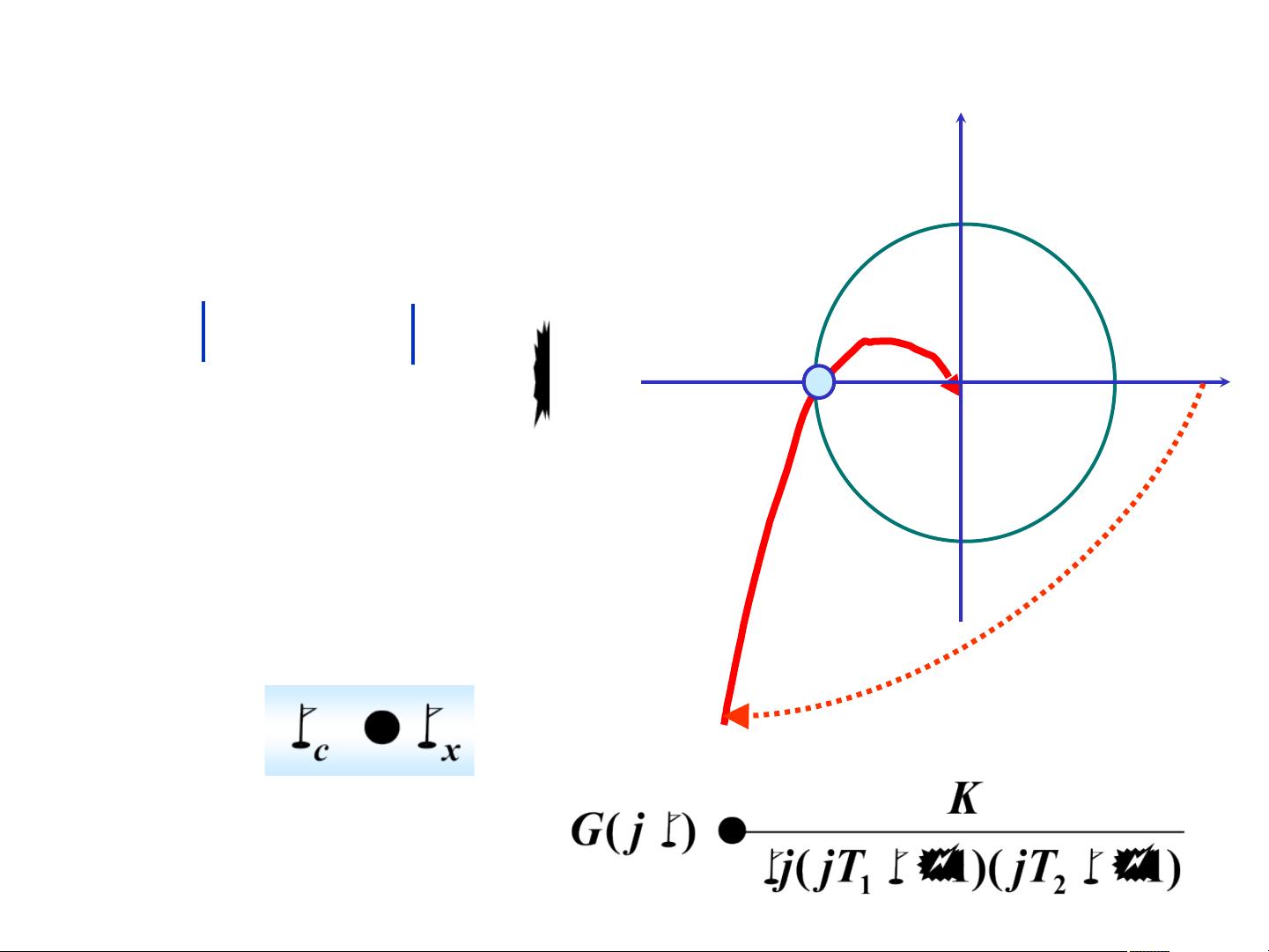
【课程大纲】 第1章 绪论 第2章 控制系统的数学模型1 第2章 控制系统的数学模型2 第2章 控制系统的数学模型3 第2章 控制系统的数学模型4 第3章 控制系统的时域分析—1引言及一阶系统时域分析 第3章 控制系统的时域分析—2二阶系统时域分析 第3章 控制系统的时域分析—3高阶系统时域分析 第3章 控制系统的时域分析—4稳定性分析 第3章 控制系统的时域分析—5稳态误差 第3章 控制系统的时域分析—5稳态误差(仿真分析不同信号作用下的稳态误差) 第4章 根轨迹1 第4章 根轨迹2 第5章 频率响应法1 第5章 频率响应法2 第5章 频率响应法3 第5章 频率响应法4 第6章 线性系统的校正方法1 第6章 线性系统的校正方法2 第6章 线性系统的校正方法3 ### 自动控制系统原理：频率响应法中的频域稳定裕度 #### 1. 频域稳定裕度的概念 在自动控制理论中，系统稳定性的评估不仅局限于时域内，还包括频域内的评估方法。其中，“频域稳定裕度”是评价系统相对稳定性的关键指标之一，它通过开环系统的频率特性来描述闭环系统的稳定性。稳定裕度主要包括两个方面：相角裕度（Phase Margin, PM）和幅值裕度（Gain Margin, GM）。这些指标能够帮助工程师判断系统是否稳定以及稳定性的优劣。 #### 2. 相角裕度 **定义**： - **相角裕度（PM）**：当系统的开环频率特性曲线在0dB线上时（即增益为1），其相角偏离-180°的程度。具体来说，它是从-180°到实际相角之间的角度差。 - **物理意义**：相角裕度反映了系统在达到临界稳定之前还能承受的最大相位滞后。如果相角裕度为正，系统是稳定的；如果为负，则系统不稳定。 **示例**： - 若某系统的相角裕度为45°，则意味着即使其相位再滞后45°，系统仍能保持稳定。 #### 3. 幅值裕度 **定义**： - **幅值裕度（GM）**：当系统的开环频率特性曲线相角为-180°时，其增益（以分贝表示）与0dB之间的差值。具体而言，它是增益曲线在-180°相角处的垂直距离。 - **物理意义**：幅值裕度反映了系统在达到临界稳定之前还能承受的最大增益增加量。如果幅值裕度为正，系统是稳定的；如果为负，则系统不稳定。 **示例**： - 若某系统的幅值裕度为10dB，这意味着即使增益再增加10dB，系统仍然能够保持稳定。 #### 4. 稳定裕度的应用 在工程实践中，通常需要确保相角裕度和幅值裕度均为正，以保证系统的稳定性。一般推荐的数值范围是相角裕度在30°至60°之间，幅值裕度大于6dB。这样的设计可以提高系统的鲁棒性，使其在面对参数变化时更加稳定可靠。 #### 5. 稳定裕度的具体计算 - **计算相角裕度**：首先找到系统的截止频率ωc（即增益为0dB时的频率），然后计算在该频率下的相角与-180°的差值。 - **计算幅值裕度**：找到系统相角为-180°时的频率ωx，然后计算在此频率下的增益与0dB的差值。 **实例解析**： **例1**：考虑一个单位负反馈二阶系统的开环传递函数为\[G(s) = \frac{k}{s^2 + 2\zeta s + 1}\]，计算相位裕量与阻尼比ζ的关系。 - **解答**：根据开环传递函数计算截止频率ωc，然后利用ωc计算在该频率下的相角，最后得到相角裕度。 **例2**：给定系统的开环传递函数\[G(s) = \frac{k}{s(s+1)}\]，计算K=5、20时的相角裕度和幅值裕度。 - **解答**：当K=5时，可通过绘制Nyquist图或Bode图读取相角裕度和幅值裕度；当K=20时，同样通过图解法或近似计算法获得相应的稳定裕度。 #### 6. “三频段”概念 在开环对数幅频特性中，还存在“三频段”的概念，即低频段、中频段和高频段。这三个频段分别对应系统在不同频率范围内的行为特征，有助于更全面地理解系统的性能和稳定性。 - **低频段**：主要反映系统的静态性能。 - **中频段**：与系统的动态性能（如响应速度和稳定性）有关。 - **高频段**：涉及系统的抗干扰能力和噪声抑制能力。 通过对这些概念的理解和应用，工程师能够在设计自动控制系统时做出更加合理的决策，确保系统的稳定性和可靠性。