前馈神经网络调研
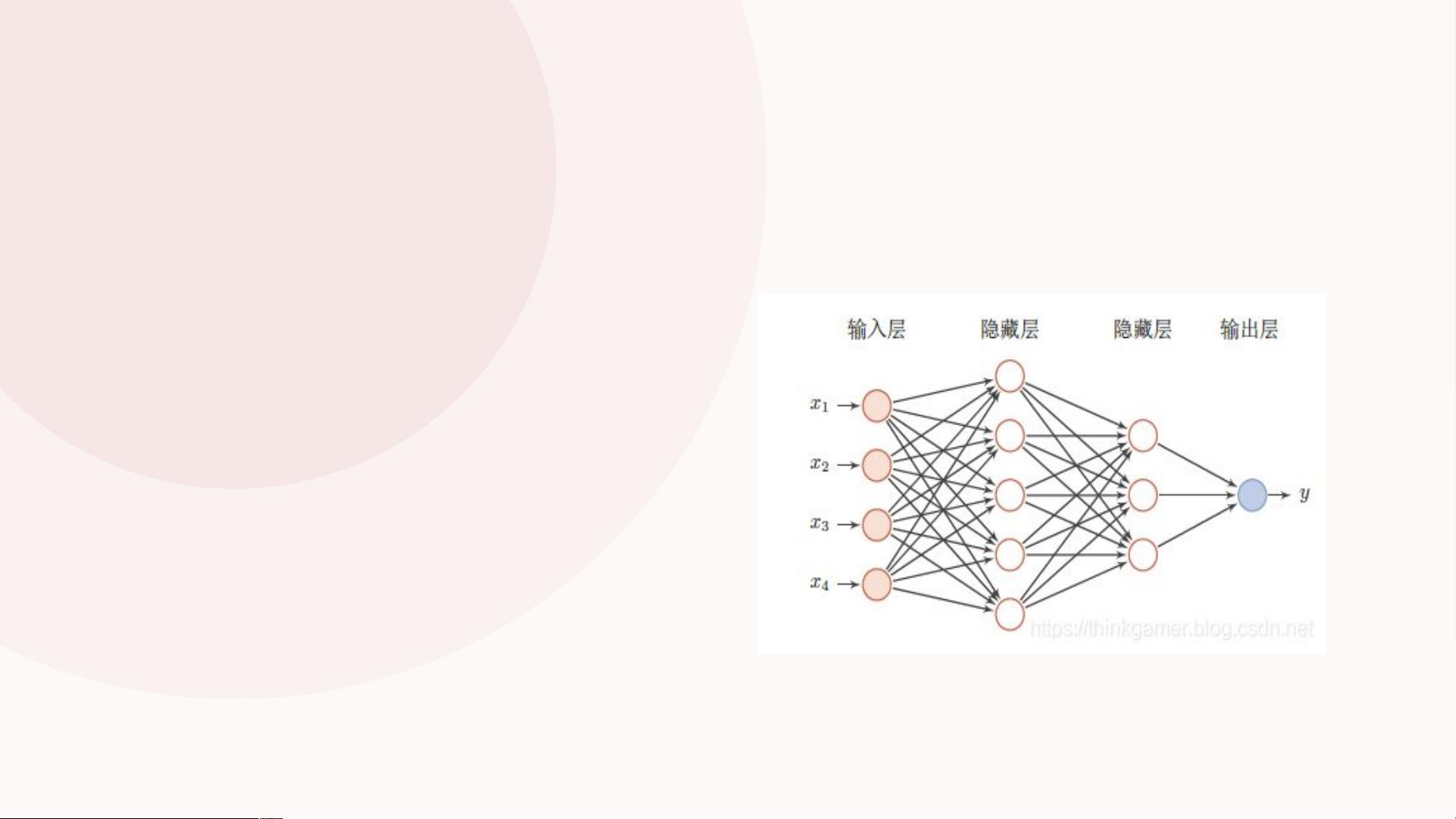
前馈神经网络(Feedforward Neural Network,FNN)是一种简单的人工神经网络类型,在人工智能领域中最早发明。它内部,参数从输入层经过隐含层向输出层单向传播,不会构成有向环。FNN 由一个输入层、一个(浅层网络)或多个(深层网络)隐藏层,和一个输出层构成。每个层(除输出层以外)与下一层连接,这种连接是 FNN 架构的关键,具有两个主要特征:加权平均值和激活函数。
FNN 的数据传播是将向量 x 作为第一层的输入 a^0,将第 l 层的输入 a^l,将第 L 层的输出 a^L 作为整个函数的输出。传播公式为:
a^l = f(W^l * a^(l-1) + b^l)
也即:
a^L = f(W^L * a^(L-1) + b^L)
最后输出函数:
f(x) = a^L
多层感知器(Multilayer Perceptron,MLP)程序的执行流程如下:
计算隐层单元的输出(利用输入单元和隐层单元到输入层单元的权值);然后,继续计算下一层(这里指输出层)单元的输出。通常这个过程被称为前向传送数据,或简单的称之为前馈(feed forward)。
可以把神经网络看成并行计算系统。每个神经元是一个处理元件,该处理元件接受一个或多个输入并产生一个输出,输入和输出均可以看成信息。在多层感知器架构中,输出可以被送往多个其他处理单元,做进一步的处理。神经网络并行性的特性来自于同一层多个神经元之间的并行性。所有的神经元能够同时处理它们各自的输入,使得在多处理器系统中同一层次上具有大量神经元的神经网络的运行速度更快。
激活函数定义了该节点在给定的输入或输入的集合下的输出,就是决定信息是否要传输到下一层。线性激活函数是一种简单的线性函数,公式为:f(x) = x。基本上,输入到输出过程中不经过修改。
非线性激活函数用于分离非线性可分的数据,是最常用的激活函数。非线性方程控制输入到输出的映射。为了解决非线性的分类或回归问题,我们的激活函数必须是非线性的函数,另外我们使用基于梯度的方式来训练模型,因此激活函数也必须是连续可导的。
常见的非线性激活函数包括Sigmoid 激活函数、Tanh 激活函数和ReLU 激活函数。Sigmoid 函数就是 Logistic 函数,其数学表达式为:
f(x) = 1 / (1 + exp(-x))
对应函数图像为:
导函数为:
f'(x) = f(x) * (1 - f(x))
Sigmoid 激活函数在定义域上是单调递增的,越靠近两端变化越平缓,而这会导致我们在使用 BP 算法的时候出现梯度消失的问题。
Tanh 激活函数就是双曲正切激活函数,其数学表达式为:
f(x) = 2 / (1 + exp(-2x)) - 1
对应函数图像为:
导函数为:
f'(x) = 1 - f(x)^2
tanh 函数几乎在任何情况下效果都比sigmoid 要好。tanh 函数的值在 -1 和 1之间,输出的结果的平均值为 0 。
ReLU 激活函数又称为修正线性单元或整流性单元函数,是目前使用比较多的激活函数,其数学表达式:
f(z) = max(0, z)
对应函数图像为:
导函数为:
f'(z) = 1 (z > 0)
ReLU 函数是非线性激活函数的默认选择,ReLU 激活函数的 X 轴左侧值恒为 0,使得网络具有一定的稀疏性,从而减少参数之间的依存关系,缓解了过拟合的情况,而且它的导函数有部分为常数 1,因此不存在梯度消失的问题。
感知机算法感知机算法中包含了前向传播(FP)和反向传播(BP)。前向传播是指计算每层的输出,然后将输出传递给下一层,以此类推,直到输出层。反向传播是指计算每层的误差,然后将误差传递给上一层,以此类推,直到输入层。
前馈神经网络是一种简单的人工神经网络类型,它的架构简单、易于实现、计算效率高,是机器学习和人工智能领域中最基本的神经网络类型。但是,它也存在一些缺陷,例如只能用于线性可分的问题,训练时间长,且对数据的要求很高。

















评论0