(一)信号
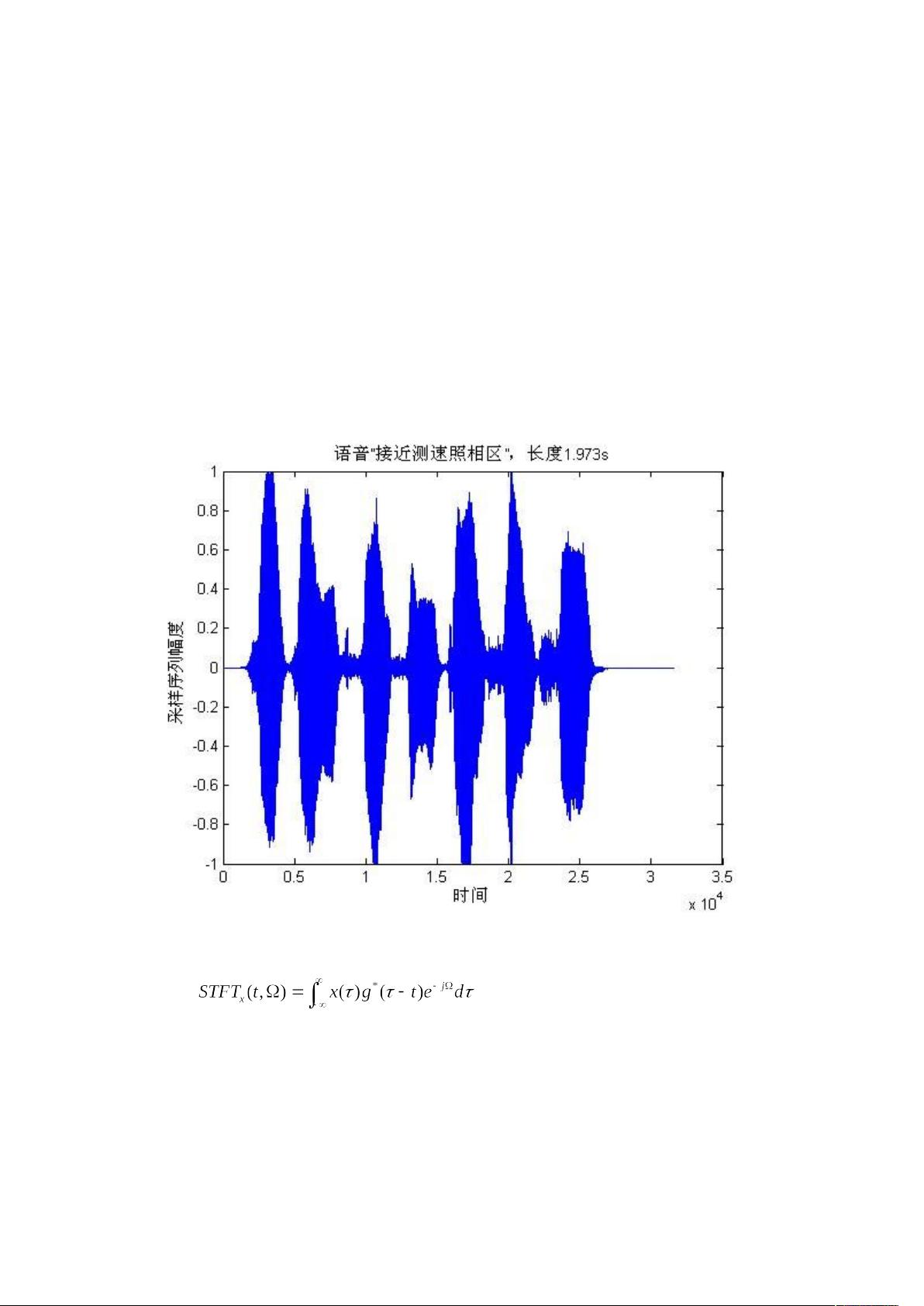
一段语音信号(一个词或词组,2秒左右),采样频率应在8kHz以上。
(二)要求
1. 分别用MATLAB作出短时傅立叶变换、Wigner-Ville分布和小波变换的时频分布图;
2. 列出公式,画出所有图谱;
3. 讨论三种时频分布的结果与特点。
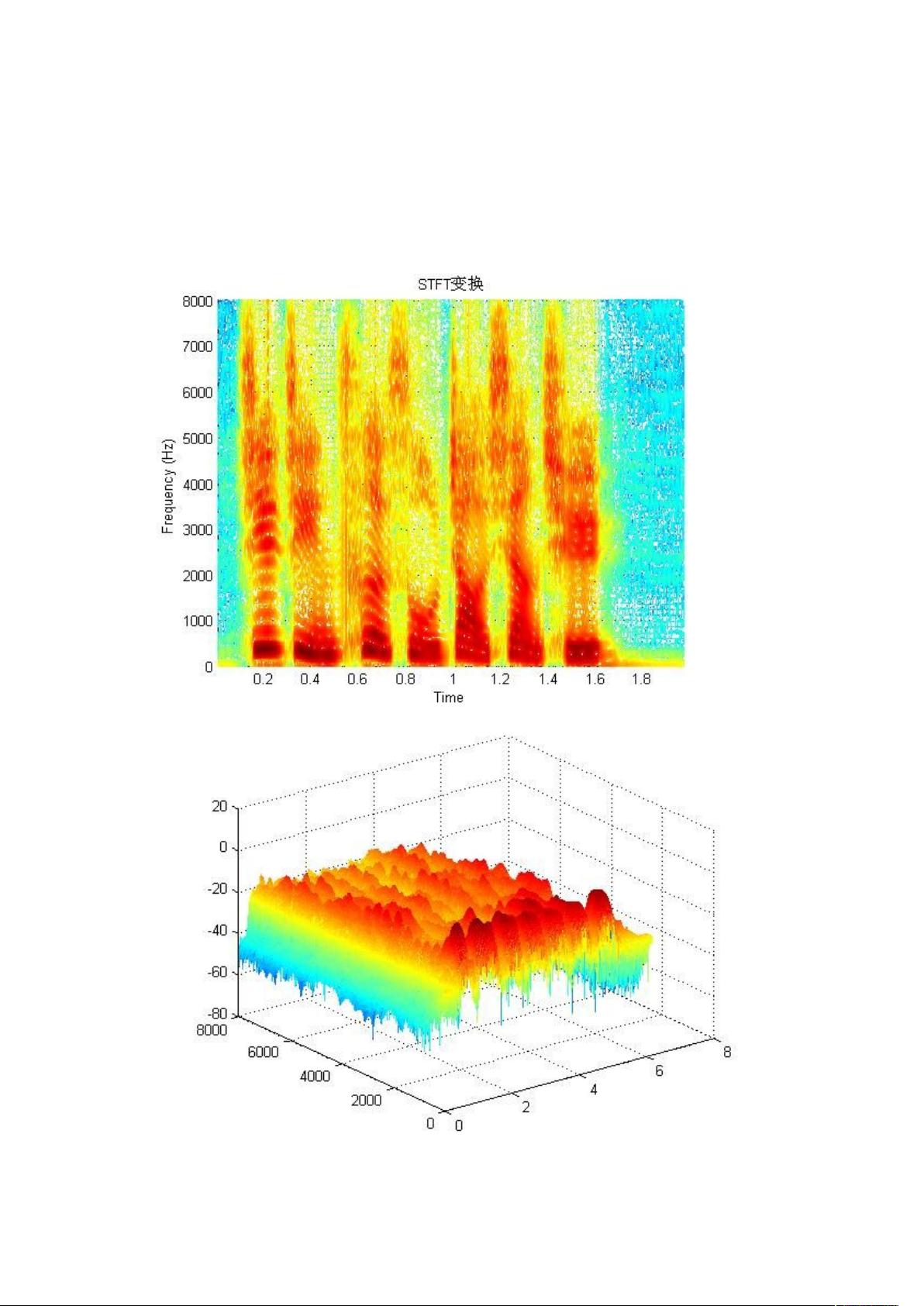
【短时傅立叶变换(Short-Time Fourier Transform, STFT)】
短时傅立叶变换是一种分析非平稳信号的方法,它通过将信号与一个局部化窗口函数(如汉明窗、哈特莱窗等)相乘,然后对每一窗口进行傅立叶变换,从而得到信号在不同时间区间的频谱特性。这种方法可以捕捉信号在短时间内随时间变化的频率信息。在MATLAB中,可以使用`tfrstft`函数实现STFT,例如:
```matlab
nfft = 512;
[x,fs,nbits]=wavread('T01.wav');
n = length(x);
STFT[tfr1,t1,f1]=tfrstft(x,1:10:n,nfft);
```
【Wigner-Ville分布(Wigner-Ville Distribution, WVD)】
Wigner-Ville分布是最早的时频分析方法之一,它可以提供信号在时间和频率上的局部能量分布,但可能会出现交叉项干扰,导致“斑点”现象。WVD是自相关函数和傅立叶变换的卷积,对于理解信号的局部性质非常有用。MATLAB中的`tfrwv`函数可以计算Wigner-Ville分布,如以下代码所示:
```matlab
nfft = 512;
[x,fs,bits1]=wavread('T01.wav');
n = length(x);
WVD[tfr2,t2,f2] = tfrwv(x,1:10:n,nfft);
```
【小波变换(Wavelet Transform)】
小波变换是一种灵活的时频分析工具,它通过使用具有不同尺度和位置的小波函数来分析信号。小波变换既保持了时间分辨率,又保持了频率分辨率,特别适合于分析非平稳信号。在MATLAB中,可以使用连续小波变换函数`cwt`来计算小波变换,如以下示例:
```matlab
nfft = 512;
[x,fs,bits1]=wavread('T01.wav');
n = length(x);
wave = cwt(x,A,'morl');
```
这里使用的是Morlet小波基,通过调整尺度参数可以改变时间-频率分辨率。
【讨论】
1. STFT提供了良好的频率分辨率,但时间分辨率受限于窗口大小。若要提高时间分辨率,必须减小窗口长度,但这会降低频率分辨率。
2. WVD提供了最精细的时频分辨率,但由于交叉项的存在,可能不适合解析复杂信号,尤其在信号重叠时。
3. 小波变换则通过调整小波基的尺度和位置,实现了动态的时间-频率分辨率,能够适应信号的不同局部特性,对于非平稳信号分析更为优越。
STFT适用于分段平稳信号的分析,WVD更适合于研究信号的精细时频结构,而小波变换则是处理非平稳信号的利器,可以根据实际需求选择合适的方法。在MATLAB中,这三个方法都可以通过绘制三维图来直观展示信号的时频分布特性。














- 1
- 2
- 3
- 4
- 5
前往页