线段树和树状数组入门介绍

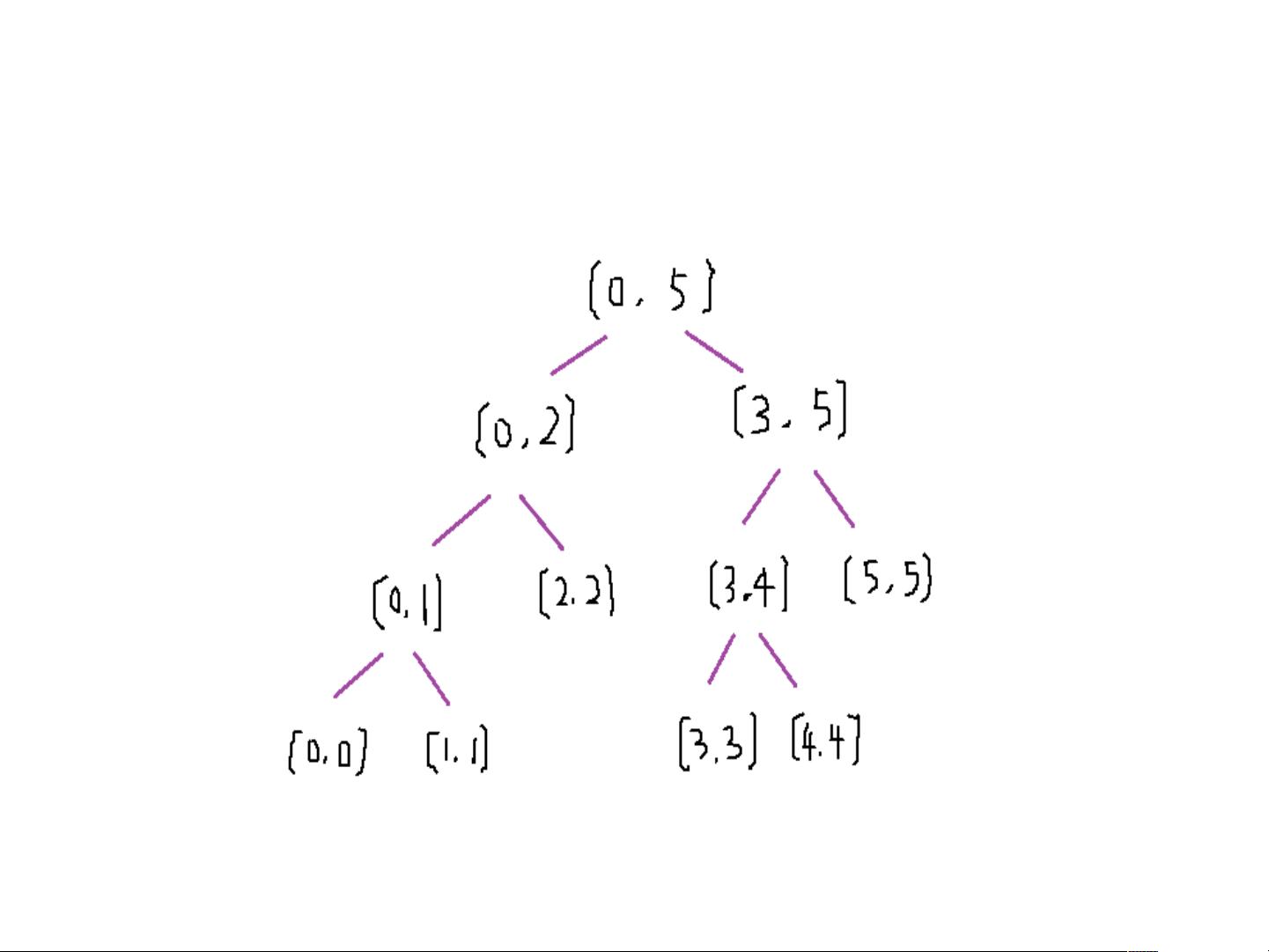
线段树和树状数组是两种在ACM（算法竞赛）和编程中广泛使用的高效数据结构，它们主要用于处理数组上的区间查询和修改操作。这里我们将深入理解这两种数据结构的原理和应用。 线段树是一种能够支持动态维护区间最值（最大值或最小值）的数据结构。在线段树中，数组元素被存储在一个二叉树中，每个节点代表一个区间的最大值。以给定的数组num[] = {3,7,6,5,6,2}为例，构建的线段树如描述所示，它能够快速查询和更新区间内的最值。线段树的空间复杂度为O(n*4)，其中n是数组的长度，每次更新和查询的时间复杂度为O(logn)。为了实现线段树，我们需要定义三个关键函数：Init用于初始化线段树，read用于查询区间最大值，update用于更新指定位置的值。这三个函数通过递归的方式操作线段树的节点，确保每次操作都在对数时间内完成。 接下来，我们来看树状数组。树状数组（也称为斐波那契堆）是一种更简洁的数据结构，用于区间求和问题。不同于线段树，树状数组利用位运算，将数组元素的索引转换为其在二进制表示下的最后一个非零位的权重，从而实现快速的区间求和。树状数组的主要优点是实现简单，代码量小，同样具有O(logn)的查询和更新时间复杂度。树状数组通常包含三个基本操作：read返回区间[1, k]的元素和，update将索引k处的值增加v，以及find_Kth返回第k大的元素。 线段树和树状数组各有优势，线段树适用于区间最值查询，而树状数组更适合区间求和。在实际应用中，应根据问题的具体需求选择合适的数据结构。例如，如果需要频繁查询区间内的最大值，线段树是理想选择；如果关心的是区间和，那么树状数组更为高效。同时，两者都可以通过扩展实现更多的功能，如区间加减操作等。 在ACM竞赛或实际编程中，熟练掌握线段树和树状数组能大大提高解决问题的效率。理解它们的基本原理，并通过实践编写代码来加深理解，是成为优秀程序员的关键步骤。这两种数据结构都是算法工具箱中的重要成员，值得深入研究和灵活运用。