ACM入门资料

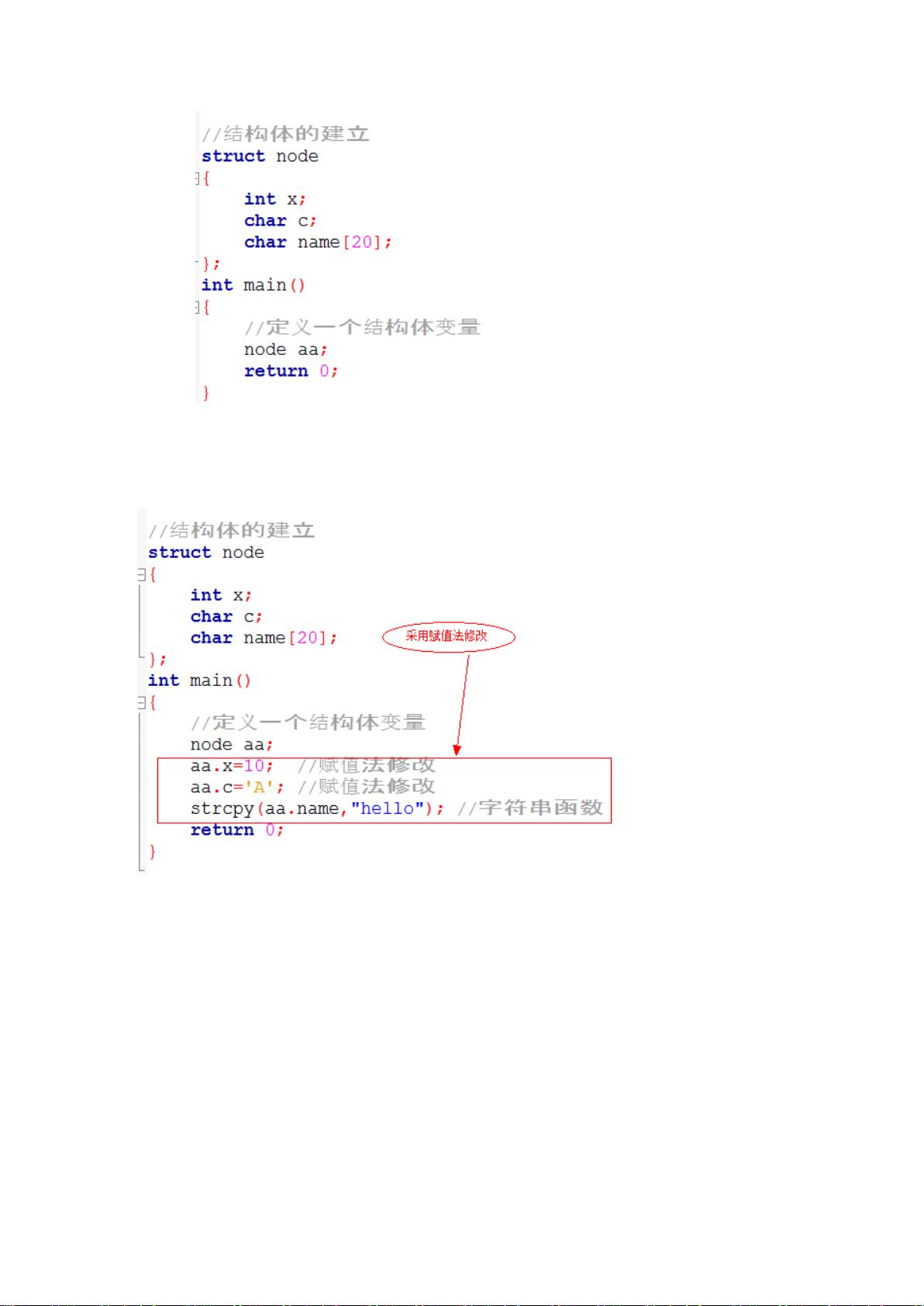
ACM竞赛是大学生计算机程序设计竞赛的简称，其内容涉及算法、数据结构等计算机科学领域的知识。在ACM入门阶段，参赛者需要掌握一系列的基础知识和技能，为解决更加复杂的问题打下坚实的基础。以下是对ACM入门资料中提到的知识点进行的详细说明。 ### 第一章 基础入门 #### 1. 结构体（Struct） 结构体是C语言中一种复合数据类型，它允许将不同类型的数据组合成一个单一的类型。结构体的定义包括数据类型、成员和数据名。通过结构体，可以更好地管理复杂的数据信息。在ACM竞赛中，结构体的使用可以提升代码的可读性和维护性。 #### 2. 函数（Function） 函数是组织好的，可重复使用的，用来执行特定任务的代码块。在ACM竞赛中，学会合理地设计和使用函数是提高编程效率的关键。函数的参数传递方式有值传递和引用传递两种，前者不会改变原数据，后者则可能改变原数据。函数的返回值是函数执行结果的输出，可以是任意类型的数据。 #### 3. 冒泡排序法（Bubble Sort） 冒泡排序是一种简单的排序算法，它重复地遍历要排序的数列，比较每对相邻元素的值，如果顺序错误就把它们交换过来。虽然冒泡排序在效率上不是最优的排序算法，但在ACM入门阶段，掌握冒泡排序是理解更复杂排序算法的基础。 #### 4. 枚举（Enumeration） 枚举是一种数据类型，用于定义一组命名的整数常量。在ACM竞赛中，枚举常用于限制变量的取值范围，例如定义方向时，可以定义北、南、东、西为不同的枚举值。了解枚举可以使代码更加清晰，并且在调试时更加方便。 #### 5. 复杂度分析（Complexity Analysis） 复杂度分析是评价算法效率的重要工具，它包括时间复杂度和空间复杂度两个方面。时间复杂度反映算法执行所需的时间量，空间复杂度反映算法执行所需的存储空间量。ACM竞赛中，复杂度分析能力是解题的关键，它可以帮助参赛者选择合适的算法来解决问题。 #### 6. 二分（Binary Search） 二分查找是一种在有序数组中查找特定元素的搜索算法。ACM竞赛中，二分查找及其扩展应用广泛，如查找第一个大于给定值的元素、找到满足条件的最小值等。掌握二分查找及其各种变体，对于解决排序和搜索问题至关重要。 ### 第二章 广度优先搜索（BFS） #### 1. 队列（Queue） 队列是数据结构中的一个重要概念，其特点是“先进先出”（FIFO）。在ACM竞赛中，广度优先搜索（BFS）算法就需要用到队列。队列的数据结构允许我们在一个有序的序列中添加和移除元素。BFS算法通过逐层向外扩展，查找最短路径或达到特定条件的节点。 #### 2. BFS的思想 BFS从一个节点开始，先访问其所有邻近的节点，然后再对这些邻近节点逐个进行同样的操作。这种搜索方式能够找到从起点到终点的最短路径，尤其是在无权图中。 #### 3. BFS的实际应用 在ACM竞赛中，BFS可以应用于求解网格问题、迷宫问题以及社交网络分析等。通过实际应用，参赛者可以进一步理解和掌握BFS算法的思想和实现方式。 ### 第三章 深度优先搜索（DFS） #### 1. 树的定义（Tree Definition） 树是一种非线性的数据结构，由节点和连接节点的边组成。树结构广泛应用于各种算法中，是ACM竞赛的基础知识之一。深度优先搜索就是一种基于树或图结构的搜索算法。 #### 2. DFS算法原理 DFS通过尽可能深地搜索树的分支来访问所有节点。如果一个节点的所有子节点都已被访问过，则回溯到上一个节点。DFS可以用来检查图中是否存在环，以及用于网络的拓扑排序。 #### 3. DFS的实际运用 DFS在解决许多图论问题中都十分有用，例如迷宫求解、电路检测、以及各种路径寻找问题。通过实践DFS算法，参赛者能加深对图和树的理解。 #### 4. DFS的时间复杂度和空间复杂度 DFS的空间复杂度主要来自于递归调用栈的大小，时间复杂度取决于图中的节点数和边数。通过分析DFS的复杂度，参赛者可以更加精确地评估算法的效率和适用场景。 #### 5. DFS的剪枝 剪枝是优化搜索算法的一种技术，通过减少不必要的搜索分支来提高效率。在DFS中，适当的剪枝策略可以显著减少算法的时间消耗，是ACM竞赛中提高解题速度的重要技巧。 ### 第四章 图论入门 #### 1. 图的相关概念 图是由顶点（Vertex）的有穷非空集合和顶点之间边的集合组成。在ACM竞赛中，图论是解题的关键知识领域之一，涉及到图的遍历、连通性、路径搜索等问题。 #### 2. 存图方式 在ACM竞赛中，图的表示方法有多种，常见的包括邻接矩阵和邻接表。选择合适的存图方式能影响到算法的效率和实现的难易。 #### 3. 最短路之Dijkstra算法 Dijkstra算法用于求解带权重图中的单源最短路径问题。算法的基本思想是贪心策略，通过不断选择最短距离的顶点来更新其他顶点的距离。 #### 4. 最小生成树之Prim算法 Prim算法是用于求解最小生成树的算法，它适用于带权重的连通图。最小生成树是一种包含图中所有顶点且边的权重之和最小的子图。 ### 第五章 动态规划入门 #### 1. 基本思想 动态规划是一种将复杂问题分解为简单子问题求解的方法，通过保存子问题的解来避免重复计算。动态规划适用于具有重叠子问题和最优子结构特性的动态优化问题。 #### 2. 数字三角形 数字三角形问题是动态规划的经典应用之一。这类问题通常包含一个数字三角形，要求从顶部到底部的最优路径，使得路径上的数字总和最大。 #### 3. 最大子段和 最大子段和问题是寻找一维数组中和最大的连续子数组。动态规划可以用来解决这个问题，其核心思想是维护一个包含到当前位置为止的最大子段和的数组。 #### 4. 最长上升序列 最长上升序列问题要求在一系列数中找出一个最长的递增子序列。动态规划可以用来高效地解决这个问题，通过存储每个位置的最大上升序列长度来得到最终答案。 ### 第六章 数据结构入门 #### 1. 并查集 并查集是一种数据结构，用于处理一些不交集的合并及查询问题。并查集可以快速地合并和判断两个元素是否属于同一个集合。 #### 2. 二叉树 二叉树是每个节点最多有两个子树的树结构，是数据组织的一种方式。二叉树的遍历、构建以及平衡二叉树等概念对于ACM竞赛解题非常重要。 #### 3. 线段树 线段树是一种二叉树状的数据结构，主要用于区间查询和区间修改问题。线段树可以高效地处理动态区间的数据查询和更新。 以上便是ACM入门资料中所涵盖的重要知识点，掌握这些内容对参与ACM竞赛有着极大的帮助。通过理论学习和实际编程练习，参赛者可以逐步提高自己的算法和编程能力。