Guided-WaveCharacteristicsCoupledMicrostripLines—EvenandOddModes资源-CSDN文库

需积分: 9 169 浏览量 2016-11-20 22:52:35 上传评论收藏 390KB PDF 举报

资源推荐

资源详情

资源评论

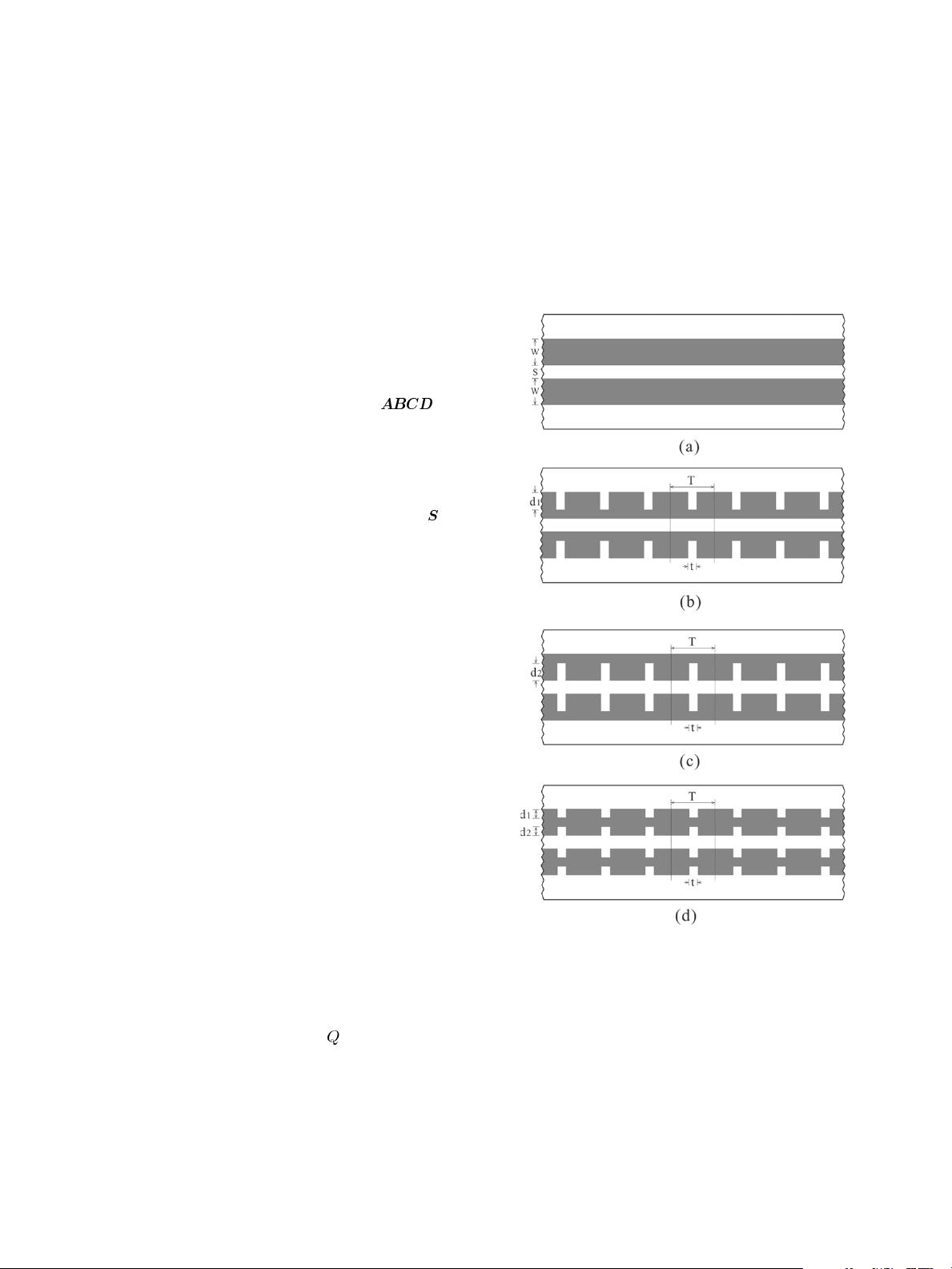
IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. 53, NO. 4, APRIL 2005 1221

Guided-Wave Characteristics of Periodically

Nonuniform Coupled Microstrip

Lines—Even and Odd Modes

Sheng Sun, Student Member, IEEE, and Lei Zhu, Senior Member, IEEE

Abstract—Even- and odd-mode guided-wave characteristics of

periodically nonuniform coupled microstrip lines (PNCML) are

thoroughly investigated in terms of the two sets of per-unit-length

transmission parameters, i.e., characteristic impedance and phase

constant. By executing the short-open calibration (SOC) procedure

in the method-of-moments platform, the two-port

ma-

trices of the PNCML with ﬁnite unit cells are numerically deem-

bedded via two sets of SOC standards so as to explicitly derive

the effective per-unit-length parameters. After our investigation

on the behaviors of numerical convergence, extensive results are

derived to demonstrate the frequency- and periodicity-dependent

per-unit-length parameters of the three types of PNCML against

those of the uniform coupled microstrip line. In ﬁnal, the

-pa-

rameters of a PNCML circuit are directly simulated via extracted

per-unit-length parameters and they are validated in magnitude

and phase by those from the Momentum simulator.

Index Terms—Even mode, method of moments (MoM), odd

mode, periodically nonuniform coupled microstrip line (PNCML),

per-unit-length transmission parameters, short-open calibration

(SOC).

I. INTRODUCTION

OUPLED microstrip lines (CMLs) with two strip conduc-

tors placed parallel in close proximity with each other, as

illustrated in Fig. 1(a), have been extensively studied and uti-

lized as basic circuit elements for directional couplers, bandpass

ﬁlters, etc. [1]. Due to the inhomogeneous dielectric medium,

the two dominant modes, i.e., even and odd modes, exist in

this CML with different velocities of propagation. This non-

synchronous feature deteriorates the performances of microstrip

circuits using the uniform CML, such as low directivity in direc-

tional coupler [2] and spurious harmonic passband in a bandpass

ﬁlter [3]. Extensive research has been done thus far toward the

equalization of propagating velocities for these two modes at

certain frequencies by forming periodically varied coupled-slot

conﬁgurations, e.g., wiggly line [2], [4], zigzag line [5], corru-

gated line [3], [6]. On the other hand, these periodic structures

are strongly expected to miniaturize the overall size of various

microwave circuits by using their slow-wave behavior at the cost

of extra transmission loss with a lowered

factor.

In order to investigate in depth these periodically nonuni-

form coupled microstrip lines (PNCML) for circuit design, it is

Manuscript received May 11, 2004; revised July 15, 2004 and August 5, 2004.

The authors are with the School of Electrical and Electronic

Engineering, Nanyang Technological University, Singapore 639798 (e-mail:

ezhul@ntu.edu.sg).

Digital Object Identiﬁer 10.1109/TMTT.2005.845709

Fig. 1. Geometry of the uniform and various PNCMLs to be considered.

(a) Uniform CML. (b) PNCML (A). (c) PNCML (B). (d) PNCML (C).

commonly recognized as the most critical issue to characterize

the fundamental per-unit-length transmission parameters of the

even and odd modes, i.e., phase constants and characteristic

impedances. Under the static assumption that each periodic

unit is extremely shorter than the wavelength, propagating ve-

locities and characteristic impedances of the coupled striplines

were approximately obtained via cascaded lumped capaci-

tances and inductances [4]. According to Floquet’s theorem,

the two-dimensional (2-D) spectral-domain method of mo-

ments (MoM) was developed without including complicated

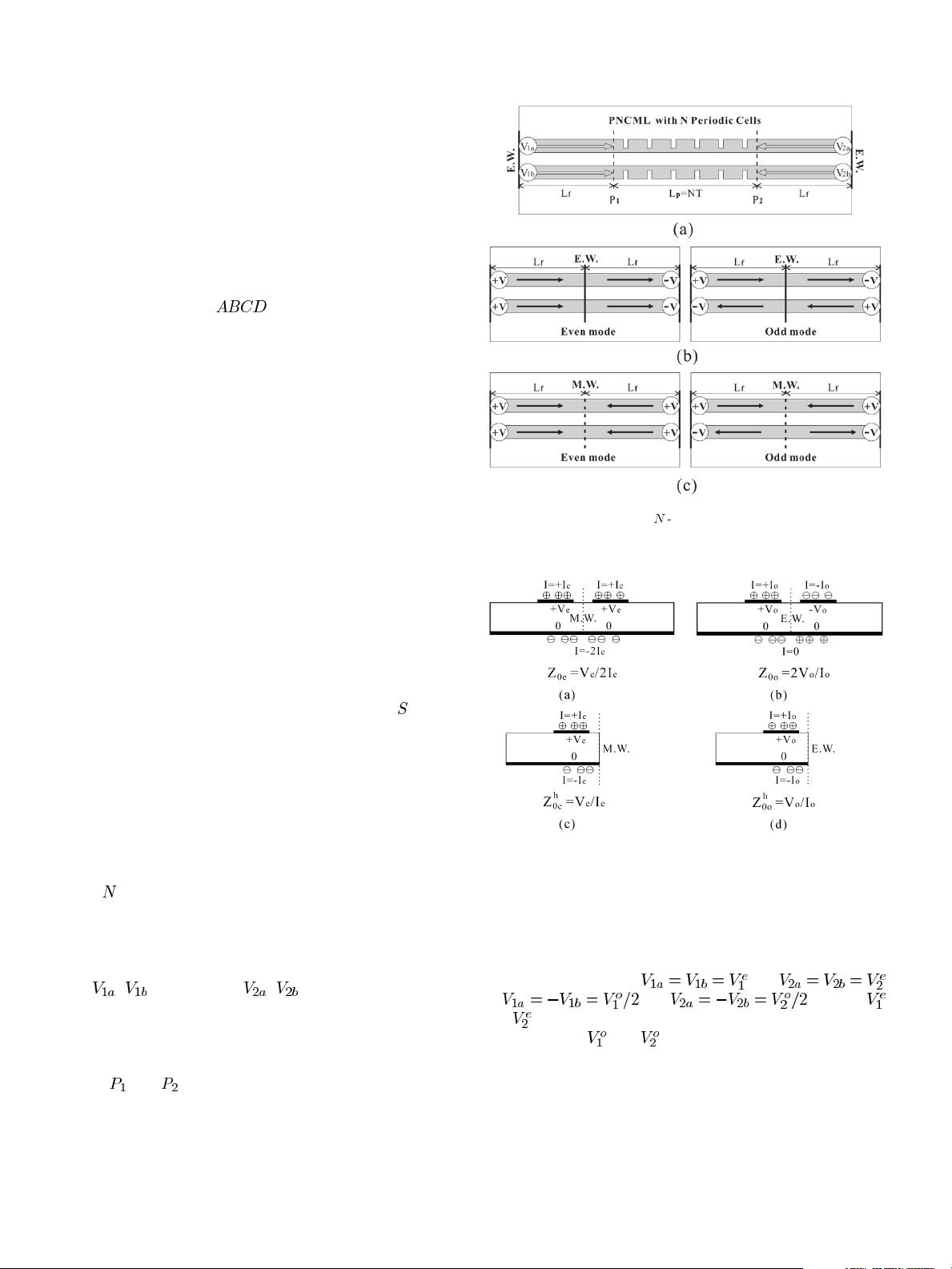
1222 IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES, VOL. 53, NO. 4, APRIL 2005

three-dimensional (3-D) effects to calculate the only phase

constant of the two modes in PNCMLs [5]. Recently, the

ﬁnite-difference time-domain (FDTD) method was employed

to obtain the even- and odd-mode phase constants of PNCMLs

[6]. However, to our knowledge, no research to date has been

reported to directly model the characteristic impedances of

these two propagating modes in any PNCML structure with the

3-D full-wave approaches [6]. Following the description in [7],

these impedances are, in fact, referred to as the characteristic

impedances of the forward or backward Bloch waves, and they

are usually deﬁned via

-matrix parameters or terminal

currents/voltages of a single periodical unit cell.

In this paper, the ﬁnite-cell PNCML driven by the uniform

CML lines at its two sides is characterized in the full-wave

MoM platform and, further, the effective per-unit-wavelength

transmission parameters of the even and odd modes propagating

along the PNCML are extracted via the short-open calibration

(SOC) technique [8]. In the past, this hybrid technique has been

utilized in accurate characterization of microstrip circuits with

single and multiple propagating modes at each single physical

port [8]–[10]. Moreover, this technique has been very recently

applied to extract the characteristic impedances and propaga-

tion constants of periodically inductive-loaded coplanar wave-

guides (CPWs) [11] and microstrip lines [12], as well as the

even and odd modes of the uniform CPW [13]. This MoM SOC

is extended here to characterize various PNCML structures, as

shown in Fig. 1(b)–(d), targeting the numerical extraction of

both characteristic impedances and phase constants for the two

dominant modes. Extensive results are obtained to demonstrate

the frequency- and periodicity-dependent guided-wave charac-

teristics of these PNCMLs via impedance and phase constant.

To validate our derived per-unit-length parameters,

-parame-

ters of a three-cell PNCML circuit are calculated via a trans-

mission-line theorem and are then compared with those from

the Agilent Momentum simulator

for both even- and odd-mode

cases.

II. M

OM–SOC CHARACTERIZATION OF

PNCML

Fig. 2(a) describes the physical layout arranged for

MoM–SOC modeling of a PNCML structure with ﬁnite

cells (

), which is driven by the two uniform CML feed lines.

In order to formulate a determinant admittance-type MoM

scheme, the two pairs of delta-gap sources backed by a vertical

electric wall (EW) are simultaneously introduced at the two

strip terminals of the left- and right-hand-side CML feed line,

i.e.,

, at port 1 and , at port 2. As long as the

two feed lines are selected electrically long, only the dominant

even and odd modes can reach to the central PNCML section

under consideration while the other excited higher order modes

at each port quickly attenuate and disappear at the reference

planes

and due to their frequency regions of operation

below cutoff frequencies [8].

Following our previous work in [13] in modeling the even-

and odd-mode guided-wave characteristics of the uniform CPW

[13], the even and odd modes in the uniform CML and PNCML

Advanced Design System (ADS) 2003a, Agilent Technol., Palo Alto, CA.

2003.

Fig. 2. Physical layouts of the

-cell PNCML under deembedding and the

two sets of SOC standards. (a) PNCML under deembedding. (b) Short-circuit

standards. (c) Open-circuit standards.

Fig. 3. Whole and a half symmetrical cross section of a CML structure and

their distinctive deﬁnitions of equivalent current and voltage quantities for the

even and odd modes. (a) Even mode: whole. (b) Odd mode: whole. (c) Even

mode: half. (d) Odd mode: half.

can also be separately excited in the full-wave MoM platform.

In this way, the even or odd modes can be generated by simul-

taneously enforcing that

and

or and . Herein,

and are the port voltages at ports 1 and 2 under even exci-

tation, whereas

and are the counterpart voltages under

odd excitation. As detailed in [8], the port currents at each port

for both the even and odd modes can be explicitly solved as

the solution of a MoM matrix equation with voltage sources via

numerical discretization of current densities over the strip con-

ductors.

In order to deembed the network parameters of the core

PNCML at the center of Fig. 2(a), the SOC technique [8] is

employed, relying on the even- and odd-mode SOC calibration

standards deﬁned in the MoM. Fig. 2(b) and (c) describes the

剩余6页未读，继续阅读

评论收藏

内容反馈

mayankai001

粉丝: 1
资源: 5

Guided-Wave Characteristics Coupled Microstrip Lines—Even and O...

最新资源

Guided-Wave Characteristics Coupled Microstrip Lines—Even and O...

Fundamentals of Guided-Wave Optoelectronic Devices

Unsupervised-Attention-guided-Image-to-Image-Translation-master.zip

guided-filter-code_引导滤波_

fast-guided-filter-code-v1_边缘提取_导向滤波_图像边缘提取_纹理_图像特征提取

Laravel开发-guided-image

guided-filter-code-v1.rar_guided-filter_matlab 引导滤波_图像去雾增强_引导滤波增

fast-guided-filter-code-v1_边缘提取_导向滤波_图像边缘提取_纹理_图像特征提取_源码.zip

guided-filter引导滤波进行图像处理

fast-guided-filter-code-v1_边缘提取_导向滤波_图像边缘提取_纹理_图像特征提取_源码.rar.rar

Self-Guided and Cross-Guided Learning for Few-Shot Seg.pptx

Deep-Flow-Guided-Video-Inpainting:pytorch实现的“深流引导的视频修复”（CVPR'19）

adversarially-guided-actor-critic:树

ngx-guided-tour

Guided-Missile-Modeling-Simulation:用C ++编写的制导空空导弹建模和仿真项目

033-Guided-Practice：https：ericagee.github.io033-Guided-Practice

fast-guided-filter-code-v1.rar_Fast 引导滤波_fast guided filter_引导滤波

论文研究-Wavelength-routed four-port optical router based on polymeric parallel-coupled microring routing element.pdf

fast-guided-filter-code-v1.rar_fast bootstrap_fast guided filter

drools-wb-guided-template-editor-api-6.1.0.Beta3.zip

python大作业 含爬虫、数据可视化、地图、报告、及源码（整和为一个文件）（2014-2020全国各地区原油加工量）.rar

仿真电路以及操作方法

【纯干货啊】华为IPD流程管理(完整版).pptx

信号与系统——保研复习资料.pdf

可编程语言标准IEC61131-3中文版.pdf

OFDM完整仿真过程与教程.zip

Landsat_WRS2.zip

最全的Visio形状/图形库

数字信号处理——保研复习资料.pdf

最新资源

python大作业含爬虫、数据可视化、地图、报告、及源码（整和为一个文件）（2014-2020全国各地区原油加工量）.rar