用matlab画分段函数y.docx

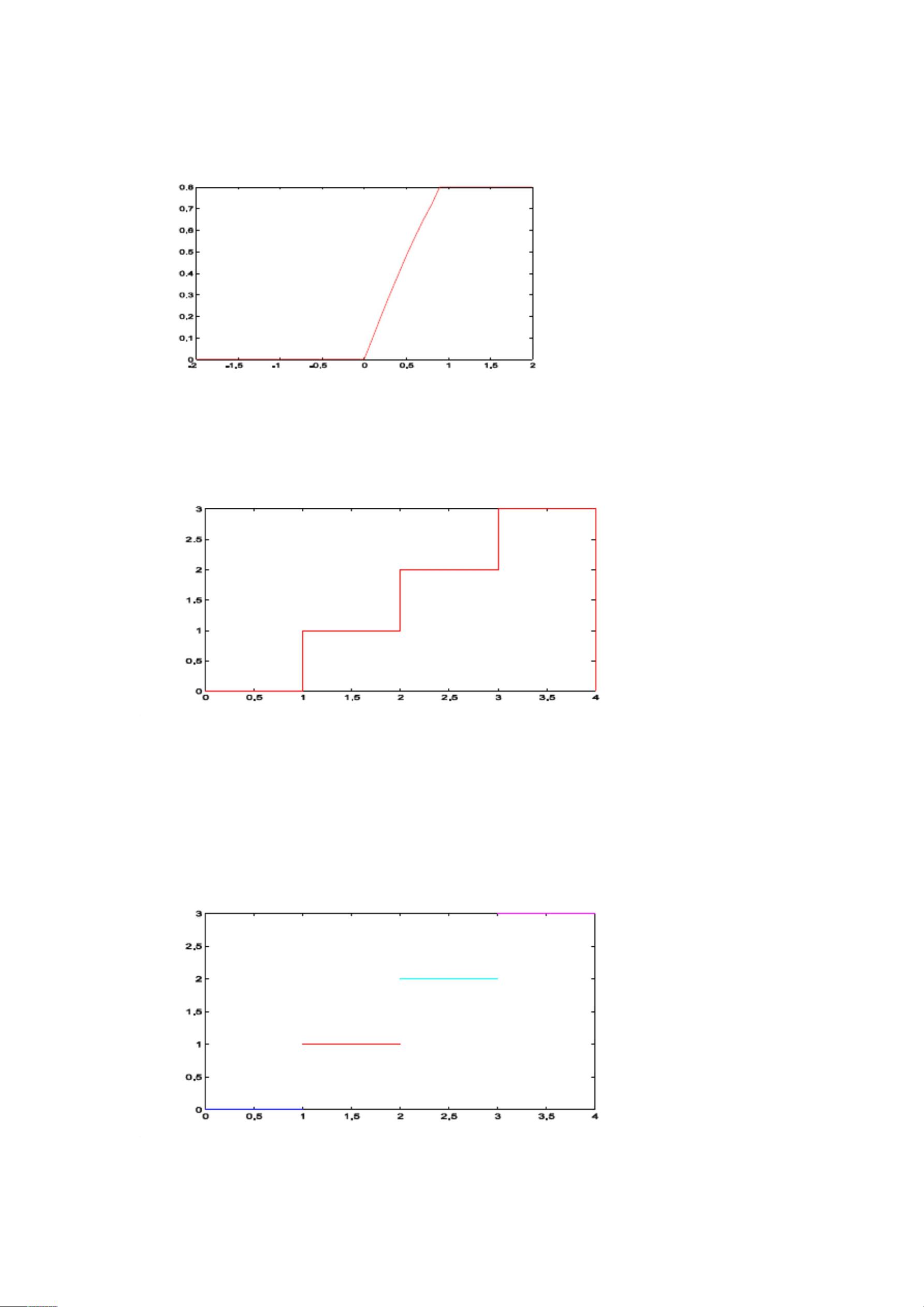
在MATLAB中绘制分段函数是一项常见的任务，它涉及到对不同条件下的函数表达式进行编程，然后使用`plot`函数来展示结果。以下是从给定的文件内容中提取的几个例子，详细解释如何使用MATLAB绘制分段函数。 **例1**：这个例子展示了如何画出一个具有三个区间的分段函数。函数`y=sin(x)`在`y<0`时被截断为`y=0`，而在`y>0.8`时被限制为`y=0.8`。MATLAB代码如下： ```matlab x = -2:0.1:2; y = 0.*(x<0) + sin(x).*(x<=0.8 & x>=0) + 0.8*(x>0.8); plot(x, y, 'r'); ``` 这里，`.*`操作符用于按元素地乘以两个向量，`&`是逻辑与运算符，用于组合两个条件。`plot(x, y, 'r')`绘制红色曲线。 **例2**：这个例子涉及高数中的取整函数`y=[x]`。函数分为四个区间：`y=0`（当`x<1`），`y=1`（当`1<=x<2`），`y=2`（当`2<=x<3`）和`y=3`（当`3<=x<4`）。MATLAB代码如下： ```matlab x = 0:0.001:4; y = 0*(x<1 & x>=0) + (x<2 & x>=1) + 2*(x<3 & x>=2) + 3*(x<4 & x>=3); % 绘制完整的曲线 plot(x, y, '-r'); % 找到边界点并分别用不同颜色画出 k1 = find(x==1); k2 = find(x==2); k3 = find(x==3); k4 = find(x==4); plot(x(1:k1-1), y(1:k1-1), 'b', ... % 蓝色部分 x(k1+1:k2-1), y(k1+1:k2-1), 'r', ... % 红色部分 x(k2+1:k3-1), y(k2+1:k3-1), 'c', ... % 青色部分 x(k3+1:k4-1), y(k3+1:k4-1), 'm'); % 紫色部分 ``` `find`函数用来查找满足特定条件的元素索引。`hold on`和`hold off`分别用于保持当前图形不被清除，以便在同一图上添加更多图形。 **例3**：此例绘制了两个分段的函数，当`x<1`时，`y=x^2`，当`x>=1`时，`y=exp(-(x-1)^2)`。代码如下： ```matlab x = -4:0.01:4; y = (x<1).*x.^2 + (x>=1).*exp(-(x-1).^2); plot(x, y, 'b'); % 添加标注 text(-2, 5, '\leftarrow y=x^2', 'FontSize', 9); text(2, 0.7, '\leftarrow y=exp(-(x-1)^2)', 'FontSize', 9); ``` `text`函数用于在图上添加文本标注，`'\leftarrow'`是箭头符号，`FontSize`参数用于设置字体大小。 通过以上三个例子，我们可以看到，MATLAB提供了强大的功能来绘制分段函数，只需要根据每个区间的函数表达式和对应的条件，用适当的逻辑操作结合`plot`函数即可实现。同时，还可以通过`text`函数添加注释，使图形更易理解。在实际操作中，可以根据需求调整步长、颜色、线条样式等参数，以获得理想的图形效果。