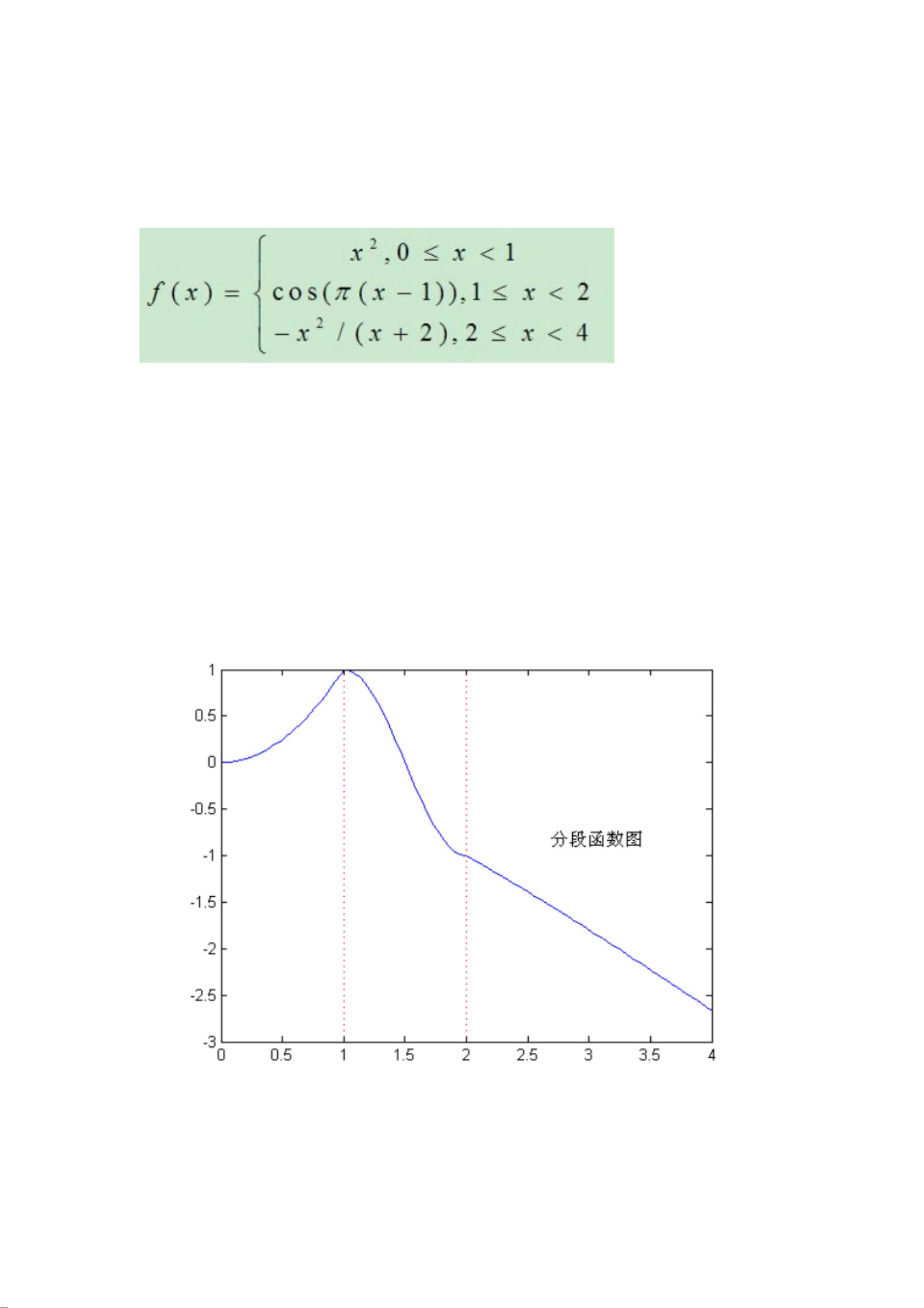
在MATLAB中,分段函数的绘图是通过编程实现的,这允许用户根据不同的条件绘制不同部分的函数。以下将详细解释如何使用MATLAB来绘制一元和二元分段函数。
我们来看一元分段函数的绘图。以给定的例子为例,函数`Piecewise_x.m`定义了一个分段函数,根据x的值,函数在不同区间有不同的表达式。代码如下:
```matlab
function F=Piecewise_x(x)
F=x.^2.*(x>=0 & x<1)+cos(pi*(x-1)).*(x>=1 & x<2)+(-x.^2./(x+2)).*(x>=2 & x<=4);
end
```
这段代码定义了一个函数F,当x在[0,1)区间时,F等于x的平方;在[1,2)区间,F等于cos(π*(x-1));在[2,4]区间,F等于-x²/(x+2)。为了绘制这个函数,我们创建一个x值的等间距数组,然后计算对应的函数值,并使用`plot`函数绘制曲线。区间间隔线用红色虚线表示,使得各区间更加明显:
```matlab
x=linspace(0,4);
F=Piecewise_x(x);
plot(x,F);
hold on;
plot(1*ones(1,2),ylim,'r:');
plot(2*ones(1,2),ylim,'r:');
```
接下来是二元分段函数的绘图。例如,`Piecewise_xy.m`文件定义了一个二元分段函数,根据x和y的值,函数在不同的区域有不同的表达式。代码如下:
```matlab
function Pxy=Piecewise_xy(x,y)
Pxy=0.5457*exp(-0.75*y^2 - 3.75*x^2 - 1.5*x).*(x+y>1)+...
0.7575*exp(-y^2 - 6*x^2).*(x+y>-1)+...
0.5457*exp(-0.75*y^2 - 3.75*x^2 + 1.5*x).*(x+y<=-1);
end
```
这个函数在(x+y>1)的区域,Pxy等于0.5457*exp(-0.75*y^2 - 3.75*x^2 - 1.5*x);在(x+y>-1)的区域,Pxy等于0.7575*exp(-y^2 - 6*x^2);在(x+y≤-1)的区域,Pxy等于0.5457*exp(-0.75*y^2 - 3.75*x^2 + 1.5*x)。为了可视化这个函数,我们创建x和y的网格,然后计算每个网格点上的函数值,并使用`mesh`函数绘制三维图像:
```matlab
[x,y]=meshgrid(-3:0.1:3);
s=size(x)
Pxy=zeros(s(1),s(2));
for i=1:s(1)
for j=1:s(2)
Pxy(i,j)=Piecewise_xy(x(i,j),y(i,j));
end
end
mesh(x,y,Pxy)
```
在这个例子中,我们使用了`meshgrid`函数来创建一个二维的x-y网格,并使用`for`循环遍历每个网格点,计算对应的Pxy值。`mesh`函数用于绘制三维网格图,展示二元分段函数的形状。
总结起来,MATLAB通过编写函数和使用适当的绘图命令,可以方便地处理和可视化一元和二元分段函数。这种能力对于理解复杂函数的行为和进行数学分析非常有用。无论是教学、研究还是工程应用,掌握MATLAB的这种功能都能大大提高工作效率。