数字信号处理-实验二-时域采样和频域采样（含能力提升和结果分析）

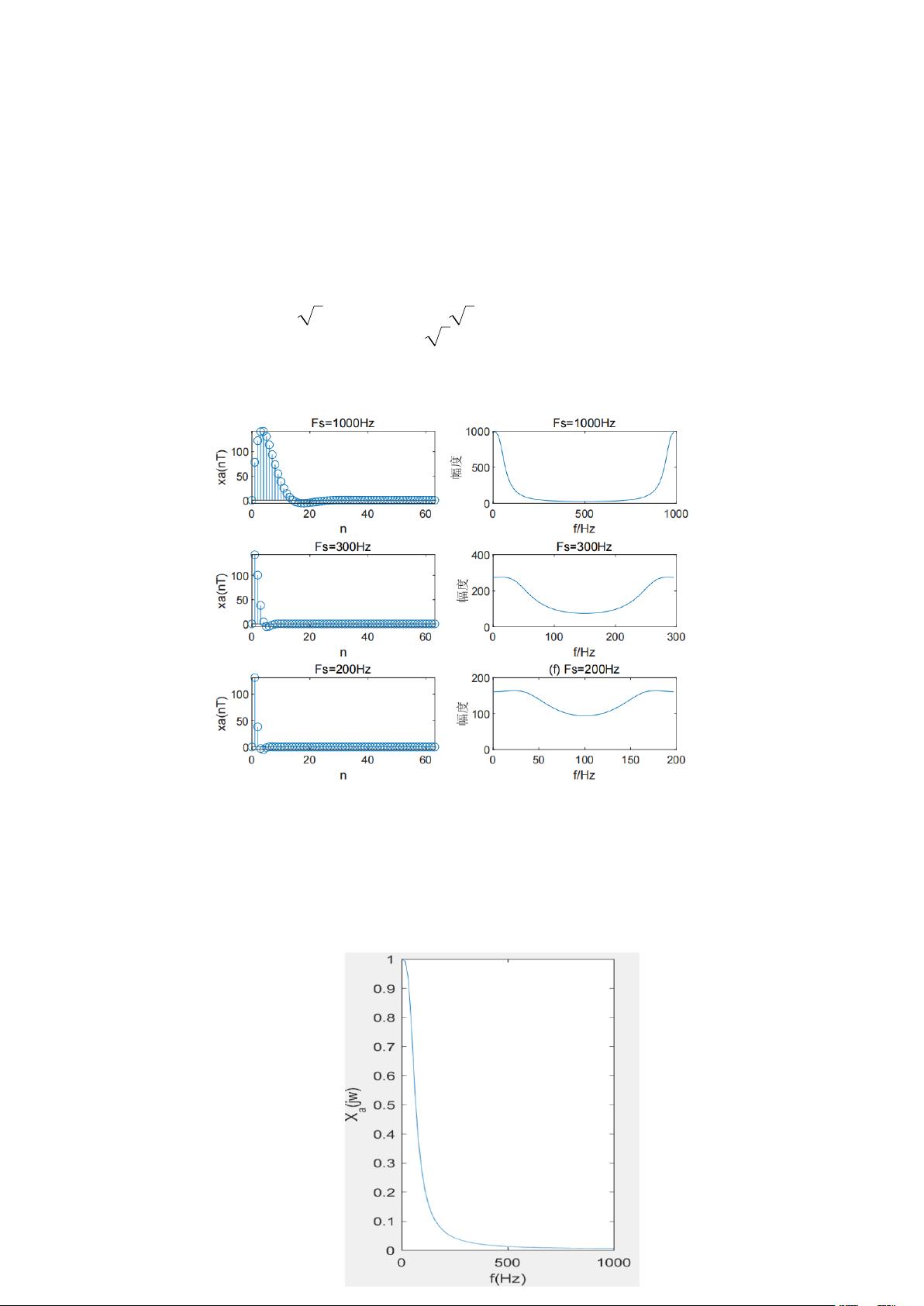
1. 时域采样定理验证。 对于模拟信号 0 ( ) sin( ) ( ) t a x t Ae t u t    ，其中： A  444.128， 50 2    ， 0 50 2 rad s    。它的幅频特性曲线如图 1 所示。信号持续时间为 T p  64ms，采样频率 F s 分别为 1kHz、300Hz、200Hz 对信号进行采用得到序列 1 2 3 ( ) ( ) ( ) x n x n x n 、 、 。 0 ( )= ( ) sin( ) ( ) nT a x n x nT Ae nT u nT    因为采样频率不同，得到的序列的长度不同， 序列长度用公式 p s M T F  计算。选 FFT 的变换点数 为 N=64，序列长度不够 64 的尾部加零。使用 FFT 对信号进行谱分析，对应频率： s k f F N  （N 为 FFT 点数，此实验中 N=64） 图 1 a () x t 的幅频特性曲线 基本要求：分别画出序列 1 2 3 ( ) ( ) ( ) x n x n x n 、 、 时域波形、频域的幅频特性曲线（横轴 《数字信号处理——时域采样与频域采样实验详解》 数字信号处理是现代通信和信息处理的核心技术之一，其中时域采样和频域采样是基础且关键的环节。本实验以模拟信号0( ) sin( ) ( ) tax t Ae t u t  为例，深入探讨这两个概念。 1. 时域采样定理的验证 时域采样定理，也称为奈奎斯特采样定理，指出为了不失真地恢复一个带限信号，采样频率Fs至少应是信号最高频率Ω0的两倍，即Fs > 2Ω0。在这个实验中，信号的最高频率Ω0 = 502πrad/s，所以最小采样频率应为4002πHz。实验中分别采用了1kHz、300Hz和200Hz的采样频率，观察到采样频率为1kHz时，频谱混叠很小；降低至300Hz时，频谱混叠严重；而进一步降至200Hz，混叠现象更加显著。这验证了采样定理的重要性，低于理论最小值会导致信号失真。 2. 信号恢复与创新挑战 通过FFT变换，可以对采样序列进行频域分析。实验展示了如何使用插值公式将采样序列恢复为原始信号。当采样频率满足奈奎斯特条件时，恢复效果良好；反之，若不满足，则恢复的信号与原始信号存在差异。例如，当采样频率为1000Hz时，恢复效果最佳，而300Hz和200Hz时，由于混叠，恢复的信号质量下降。 3. 频域采样定理的应用 频域采样定理表明，若对时域长度为M的信号进行N点IDFT，当N>M时，可能存在时域混叠失真；只有当N≥M时，才能无失真地复原信号。实验通过对比X(ejω)、X8(k)和X16(k)的图形，展示了这一原理。当N=8且N<M时，因时域混叠导致XN(n)与x(n)不同；而N=16时，N>M，XN(n)与x(n)一致，证明了频域采样定理的有效性。 MATLAB编程在实验中扮演了重要角色，通过编写代码实现了信号的时域采样、频域分析以及信号恢复。具体代码包括对不同采样频率下的信号采样，计算FFT变换，并绘制时域和频域的波形图，以及进行插值恢复。 总结来说，这个实验深入浅出地解释了时域采样和频域采样的原理，并通过实际操作展示了它们在信号处理中的应用。采样定理不仅是理论基础，也是实际工程中防止信号失真的关键指导原则。同时，频域采样定理则揭示了在频域内正确采样对于无失真恢复信号的重要性。通过实验，学生能够更好地理解和掌握这些核心概念，为后续的数字信号处理学习打下坚实的基础。