没有合适的资源？快使用搜索试试~
我知道了~
文库首页
课程资源
讲义
2625二次函数应用--几何图形的最大面积问题.ppt
2625二次函数应用--几何图形的最大面积问题.ppt
1.该资源内容由用户上传，如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款（资源遇到问题，请及时私信上传者）
版权申诉
0 下载量
112 浏览量
2021-11-13
05:43:09
上传
评论
收藏
3.99MB
PPT
举报
温馨提示
限时特惠：#19.90
39.90
VIP享9折下载
买1年送3月
2625二次函数应用--几何图形的最大面积问题.ppt
资源推荐
资源详情
资源评论
二次函数和图形最大面积学习教案.ppt
浏览：8
二次函数和图形最大面积学习教案.ppt
(2021-2022年）专题资料完美版全一册下 第二章 第12课 二次函数的应用——最值问题.ppt
浏览：159
综上所述，这些内容展示了如何利用二次函数解决实际问题，包括求解最值、优化决策、分析几何图形的性质以及经济中的利润最大化问题。在教育中，这些知识点是数学和实际应用的结合，有助于培养学生的逻辑思维和解决...
届中考数学复习方案浙教单元时二次函数的应用PPT课件.pptx
浏览：89
这篇PPT课件主要针对中考数学复习，特别是浙教版教材中的二次函数应用部分。二次函数在实际问题中扮演着重要角色，它可以帮助我们解决多种实际情境下的问题，如优化问题、几何问题以及销售策略等。 **考点1：用二次...
二次函数中动点产生的面积问题.doc
浏览：156
本课主要探讨二次函数背景下，动点引发的几何图形面积变化问题。这通常出现在中考的压轴题中，需要学生灵活运用二次函数的图象性质，以及数形结合和分类讨论的思想。 【教学目标】 1. 知识与能力：学生应能熟练应用...
二次函数的复习三角形面积.ppt
浏览：117
这篇资料主要涉及的是初中数学中的二次函数及其与几何图形结合的问题，特别是三角形面积的计算。二次函数的表达式为 y=x^2-2x-3，它与x轴的交点A、B，以及与y轴的交点C可以通过解方程得到。 1. **点A、B、C的坐标**...
二次函数与面积计算问题.ppt
浏览：32
总的来说，二次函数与面积计算问题的解决涉及到解析几何、代数和三角学的综合应用。对于每一个具体问题，都需要灵活运用这些概念，通过解方程、分析图形性质，甚至借助于图形变换来找到答案。理解和熟练掌握这些方法...
实际问题与二次函数.ppt
浏览：69
二次函数在实际问题中有着广泛的应用，特别是在解决最优化问题时。通过分析二次函数的性质，我们可以找到问题的最佳解决方案。以下是对"实际问题与二次函数"这一主题的详细阐述： 首先，二次函数的一般形式是 y = ...
263二次函数面积最值问题烛光杯课堂教学大成品.ppt
浏览：142
这篇资料主要讲解了如何运用二...这种方法在解决几何图形面积、物理中的功和能、经济学中的成本和利润等问题时非常有用。通过这样的练习，学生不仅可以深化对二次函数的理解，还能提高应用数学知识解决实际问题的能力。
第26章二次函数学习教案.ppt
浏览：93
二次函数是初中数学中的核心概念，它在解决实际问题中有着广泛的应用，特别是在优化问题和几何问题中。本教案主要围绕二次函数的概念、性质以及如何求解最大值展开。 首先，二次函数的基本形式是 y = ax^2 + bx + c...
新人教九年级上学期数学二次函数中动点图形的面积最值PPT学习教案.pptx
浏览：88
此PPT学习教案主要聚焦于如何通过解析几何的方法求解与二次函数相关的图形面积最大值问题。 首先，我们需要了解基本的二次函数形式，通常表示为`y=ax^2+bx+c`。在给定的例子中，虽然具体的函数表达式未给出，但我们...
(2021-2022年）专题资料完美版专题33：几何图形载体下的函数与几何的综合问题共14张PPT.ppt
浏览：7
例如例1中，三角形CMN的面积S与CM的长度x之间的函数表达式就是S = -x^2/2 + 2x，通过二次函数的性质可以找到S的最大值。 2. 平行线与等腰三角形： 平行线在几何问题中扮演着重要角色，它能帮助建立比例关系或者...
二次函数的应用(经典)参考.ppt
浏览：122
二次函数在数学中扮演着重要角色，特别是在解决实际问题和几何问题时。本讲座主要探讨了二次函数的应用，包括利用待定系数法确定二次函数的解析式，以及通过三种不同的形式——一般式、顶点式和交点式——来理解和...
11二次函数2.ppt
浏览：89
7. **几何应用**：在铺设地面的瓷砖问题中，通过观察图形的变化规律，我们可以发现瓷砖总数 y 与图形编号 n 的关系是二次函数 y=n²+5n+6，这说明随着 n 的增加，所需瓷砖的数量将以抛物线的方式增长。 通过以上...
二次函数中有关三角形面积问题PPT学习教案.pptx
浏览：187
这篇文档主要讲解了在中学数学中的反比例函数与二次函数在解决三角形面积问题上的应用。反比例函数是一类特殊的函数，通常表示为y=k/x（k为常数且k≠0）。它具有以下特点： 1. **概念**：反比例函数的形式为y=k/x，...
【课件】223实际问题与二次函数.ppt
浏览：24
标题和描述中提到的是关于实际问题与二次函数的应用，主要涉及如何优化存储容量以及利用有限资源最大化几何图形的面积。这些问题通常出现在数学的教学课件中，用于帮助学生理解和运用二次函数来解决实际问题。 首先...
复习二次函数.ppt
浏览：56
例如，解决最大值或最小值问题、确定物体运动轨迹、解决几何图形的面积问题等。因此，熟练掌握二次函数的图象、性质和解析式求法，是学习数学和解决实际问题的基础。通过不断练习和深入理解，我们能更好地运用二次...
专题课件完美版2020-2021资料二次函数图像与性质复习-知识点很全.ppt
浏览：185
7. **二次函数的应用题**：常涉及到解决实际问题，如距离、速度、时间问题，几何图形的面积问题等。 在例题2中，我们分析了二次函数y=—x²+x-1的性质： - 抛物线开口向下（因为a）。 - 对称轴x=-1，顶点坐标M（-1...
题型三 反比例函数与几何图形结合.ppt
浏览：89
标题中的“题型三 反比例函数与几何图形结合”指的是数学学习中的一种问题类型，主要涉及反比例函数与几何图形（如直线、三角形等）的相互关系和求解问题。这类问题通常要求学生结合函数知识和几何图形性质进行综合...
24二次函数的应用（第1课时）演示文稿 (2).ppt
浏览：103
二次函数在实际生活中有着广泛的应用，特别是在几何图形的优化设计中。本课主要探讨了如何利用二次函数来解决一些实际问题，例如最大化矩形区域的面积。以下将详细阐述相关知识点： 1. **二次函数的基本形式**：二...
人教版二次函数复习课件.ppt
浏览：111
二次函数是初中数学中的核心概念，它在方程、不等式、几何图形等领域有着广泛的应用。本复习课件主要涵盖了二次函数的概念、图象性质、图象画法以及相关问题的解决方法。 首先，二次函数的基本形式为 y=ax^2+bx+c，...
（中小学教育）中考二次函数复习课件.ppt
浏览：60
10. **应用**：二次函数广泛应用于解决实际问题中的最值问题，例如几何图形中的最大面积、最小成本等。同时，它还会与其他几何图形和动态问题相结合，要求学生理解图形的变化和不变量。 在中考复习中，掌握这些知识...
2812二次函数（2）.ppt
浏览：44
二次函数是初中数学中的核心概念，它在高中乃至大学数学中都有着广泛的应用。在二次函数中，函数形式通常表示为y = ax^2 + bx + c，其中a、b、c是常数，且a不等于0。在这个PPT中，主要探讨的是二次函数的标准形式y =...
专题课件完美版2020-2021资料二次函数存在性——直角三角形.ppt
浏览：55
本专题课件主要探讨了在直角三角形中涉及的二次函数存在性问题，以及与之相关的几何性质和解题策略。课程涵盖了以下几个核心知识点： 1. **直角三角形的存在性问题**： 在直角梯形OABC中，通过动态分析点M和N的...
专题课件（2021-2022年完美版）课时18 函数的综合应用.ppt
浏览：80
1. 二次函数与几何图形结合，如求点坐标或线段长度，需结合图形性质。 2. 与全等、相似知识结合，确定相关条件。 3. 在坐标系中，寻找线段长度、图形周长或面积的最大值或最小值，利用二次函数最值方法。 通过这些...
2623用函数观点看一元二次方程.ppt
浏览：22
通过一系列的练习和例子，学生们能更好地掌握二次函数的图象特征、方程的解的情况，以及如何将这些理论应用于解决实际几何问题。在课堂小结时，学生应该反思自己在学习过程中掌握的新技能和思维方式，以便进一步巩固...
一元二次方程应用题分类讲练优质课件[宣贯].ppt
浏览：29
在本课件中，主要讲解了关于一元二次方程在解决实际问题中的应用，特别是与几何图形相结合的问题。一元二次方程是初中数学的重要内容，它在解决面积、长度、宽度等几何问题时发挥着关键作用。下面将详细阐述相关知识...
新人教A选修生活中的优化问题举例PPT学习教案.pptx
浏览：182
这篇PPT的学习教案主要涉及了优化问题在实际生活中的应用，特别是如何通过数学方法解决存储量最大化的磁盘设计问题，以及如何通过求导法找到几何图形面积最大或最小值的问题。以下是具体的知识点总结： 1. **磁盘...
（中小学教育）一元二次方程应用题1.ppt
浏览：68
在本节以“一元二次方程应用题1”为主题的中小学教育课件中，主要讲解了如何使用一元二次方程解决实际问题，特别是与矩形面积相关的应用题。一元二次方程在数学中是一种重要的代数工具，通常表示为ax² + bx + c = 0...
浙教初中数学一次函数复习PPT课件.pptx
浏览：136
一次函数是初中数学中的核心概念，它是一种线性...这些知识点覆盖了一次函数的基础定义、性质、图象变化、平移规则以及在实际问题中的应用，是初中数学学习的重点内容。理解和掌握这些知识点对于解决相关问题至关重要。
一元二次方程的应用之动点问题PPT学习教案.pptx
浏览：75
这篇PPT学习教案主要探讨了一元二次方程在解决实际问题中的应用，特别是与动点问题相关的数学模型。首先，问题设置在海军基地的背景下，涉及三个关键点A、B和C，其中A位于B的正北200海里，B在C的正西200海里。小岛D...
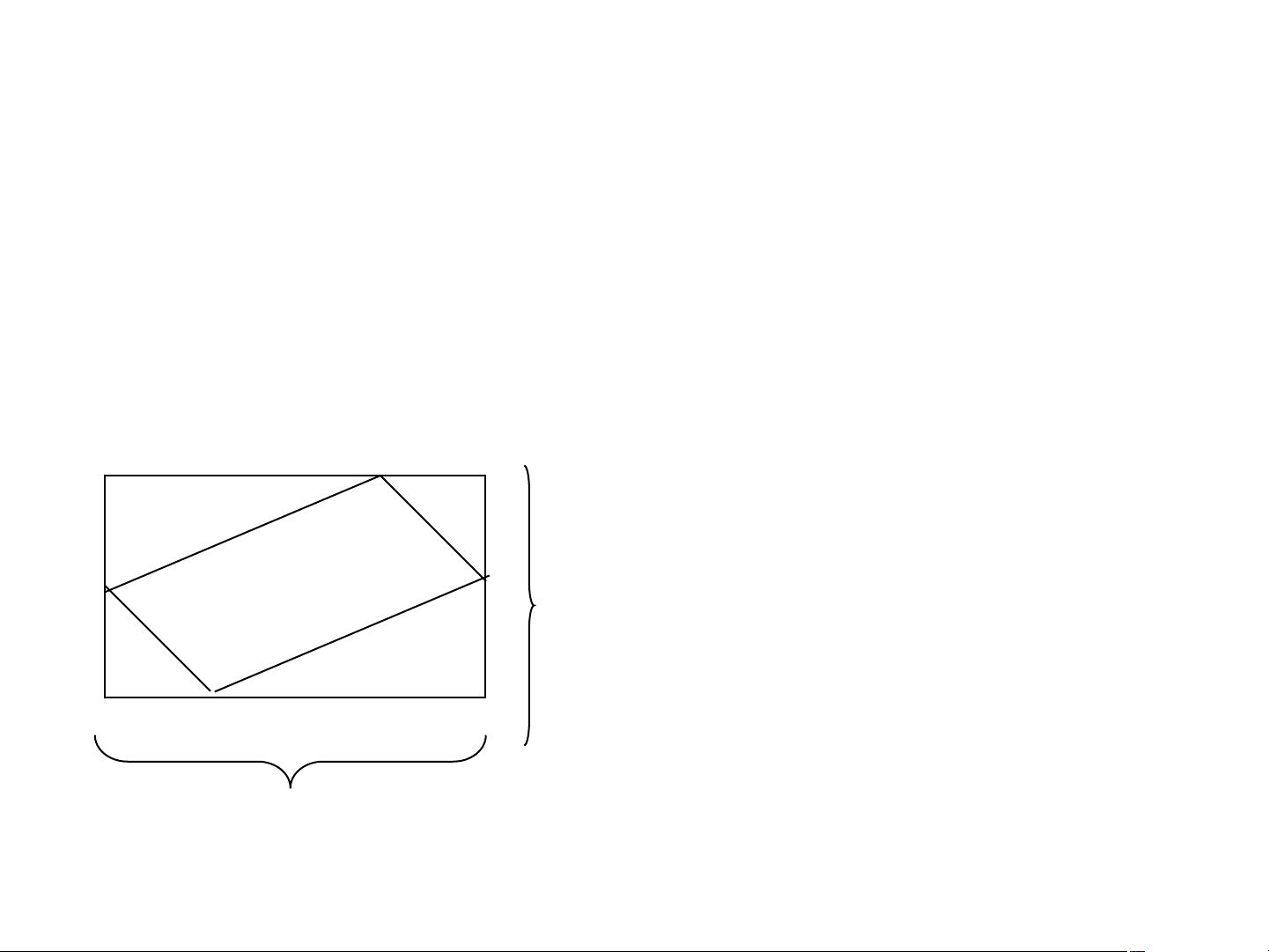
在矩形荒地ABCD中，AB=10，BC=6,
今在四边上分别选取E、F、G、H四点，且
AE=AH=CF=CG=x，建一个花园，如何设
计，可使花园面积最大？
D
C
A
B
G
H
F
E
10
6
解：设花园的面积为
y
则
y=60-x
2
-
（
10-x
）（
6-x
）
=-2x
2
+ 16x
（
0<x<6
）
=-2
（
x-4
）
2
+ 32
所以当
x=4
时
花园的最大面积为
32
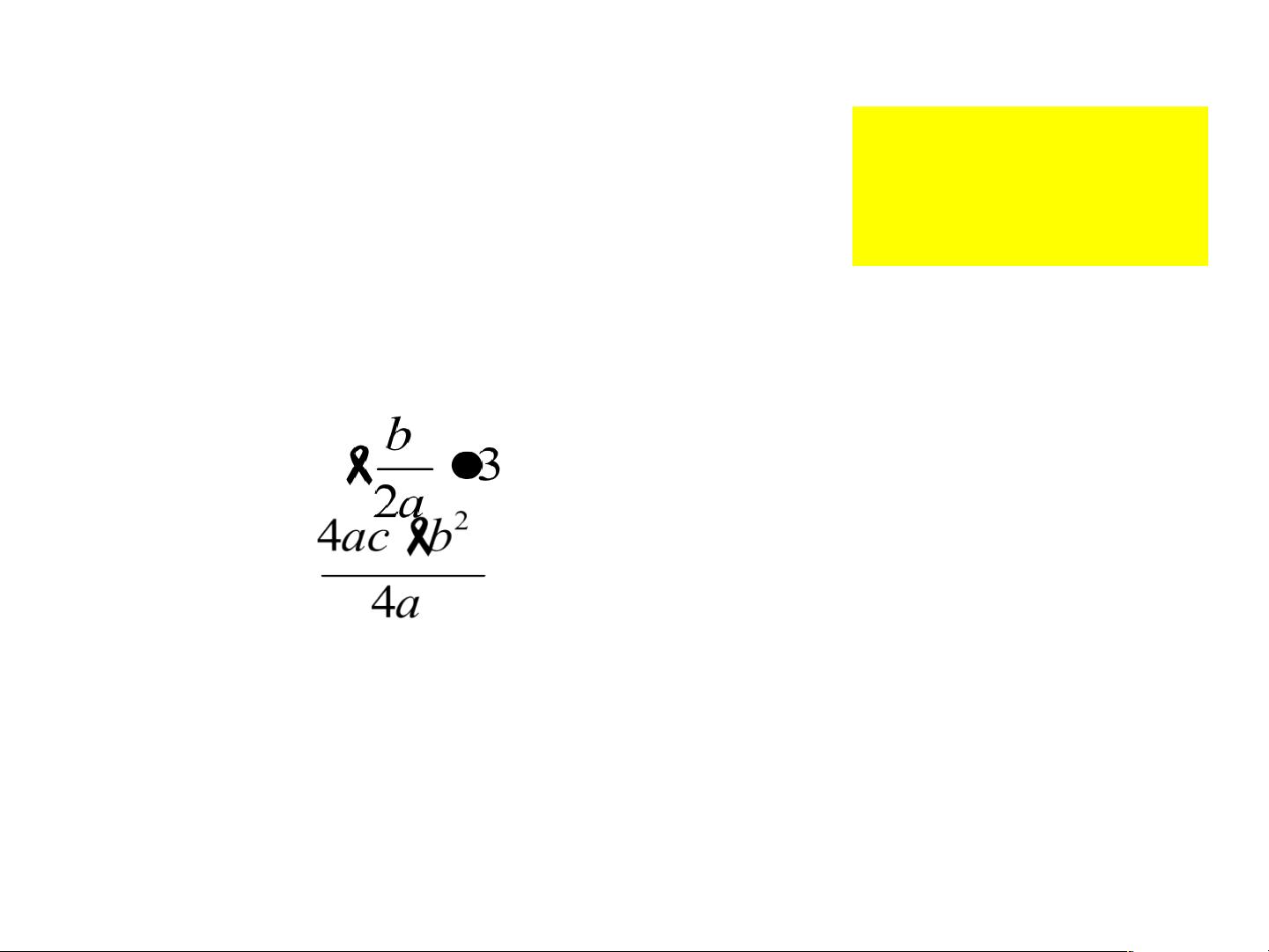
如图，在一面靠墙的空地上用长为24米的篱笆围成中间
隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，
面积为S平方米。
(1)求S与x的函数关系式及
自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积
。
A
B
C
D
A
B
C
D
解
：
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
(2)当x＝
时，
S
最大值
＝
＝36（平方米）
∴ S＝x（24－4x）
＝－4x
2
＋24 x （0<x<6）
∴ 0<24－4x ≤8 4≤x<6
∴当x＝4m时，S
最大值
＝32 平方米
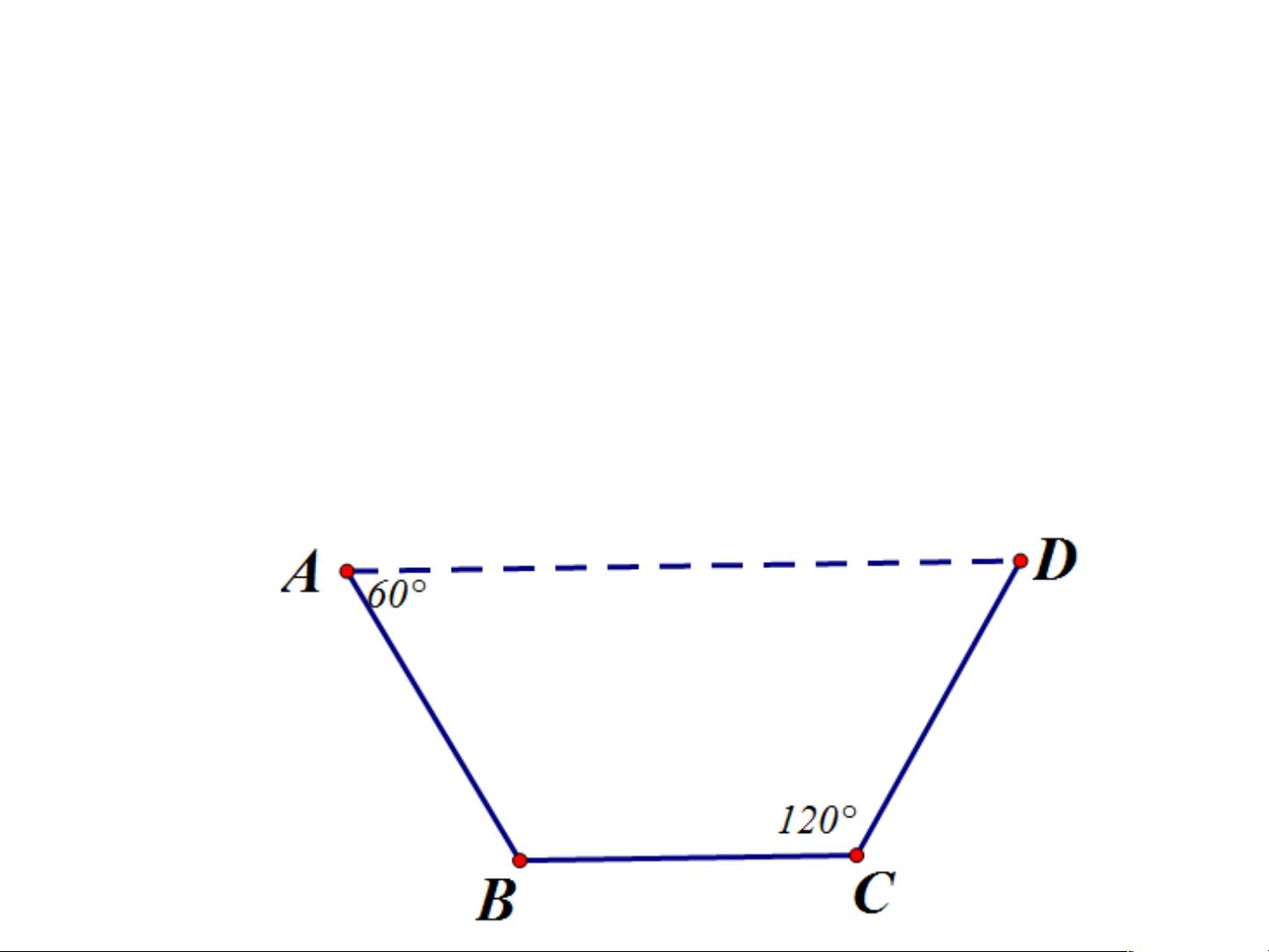
如图，某村计划修建一条水渠，其横断
面是等腰梯形，底角为120°，两腰与底
的和为6m,问应如何设计，使得横断面
的面积最大？最大面积是多少？
剩余26页未读，
继续阅读
评论
收藏
内容反馈
1.该资源内容由用户上传，如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款（资源遇到问题，请及时私信上传者）
版权申诉
限时特惠：#19.90
39.90
VIP享9折下载
买1年送3月
资源评论
资源反馈
评论星级较低，若资源使用遇到问题可联系上传者，3个工作日内问题未解决可申请退款~
联系上传者
评论
sawy5180
粉丝: 0
资源:
7万+
私信
下载权益
C知道特权
VIP文章
课程特权
VIP享
7
折，此内容立减5.97元
开通VIP
上传资源 快速赚钱
我的内容管理
展开
我的资源
快来上传第一个资源
我的收益
登录查看自己的收益
我的积分
登录查看自己的积分
我的C币
登录后查看C币余额
我的收藏
我的下载
下载帮助
前往需求广场，查看用户热搜
最新资源
(源码)基于PonyText的文本排版与预处理系统.zip
本地安装GSVA，有很多选择，我选了相对最新的
本地安装GSVA，有很多选择，我选了相对最新的
joi_240913_8.8.0_73327_share-2EM46K.apk
Library-rl78g15-fpb-1.2.1.zip
llvm-17.0.1.202406-rl78-elf.zip
学校课程软件工程常见10道题目以及答案demo
javaweb新手开发中常见的目录结构讲解
新手小白的git使用的手册入门学习demo
基于Java观察者模式的info-express多对多广播通信框架设计源码
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
安全验证
文档复制为VIP权益，开通VIP直接复制
信息提交成功
VIP享7折，此内容立减5.97元 
VIP享7折，此内容立减5.97元 VIP享7折，此内容立减5.97元 