动态过程数学模型参数估计的最小二乘方法Least.docx

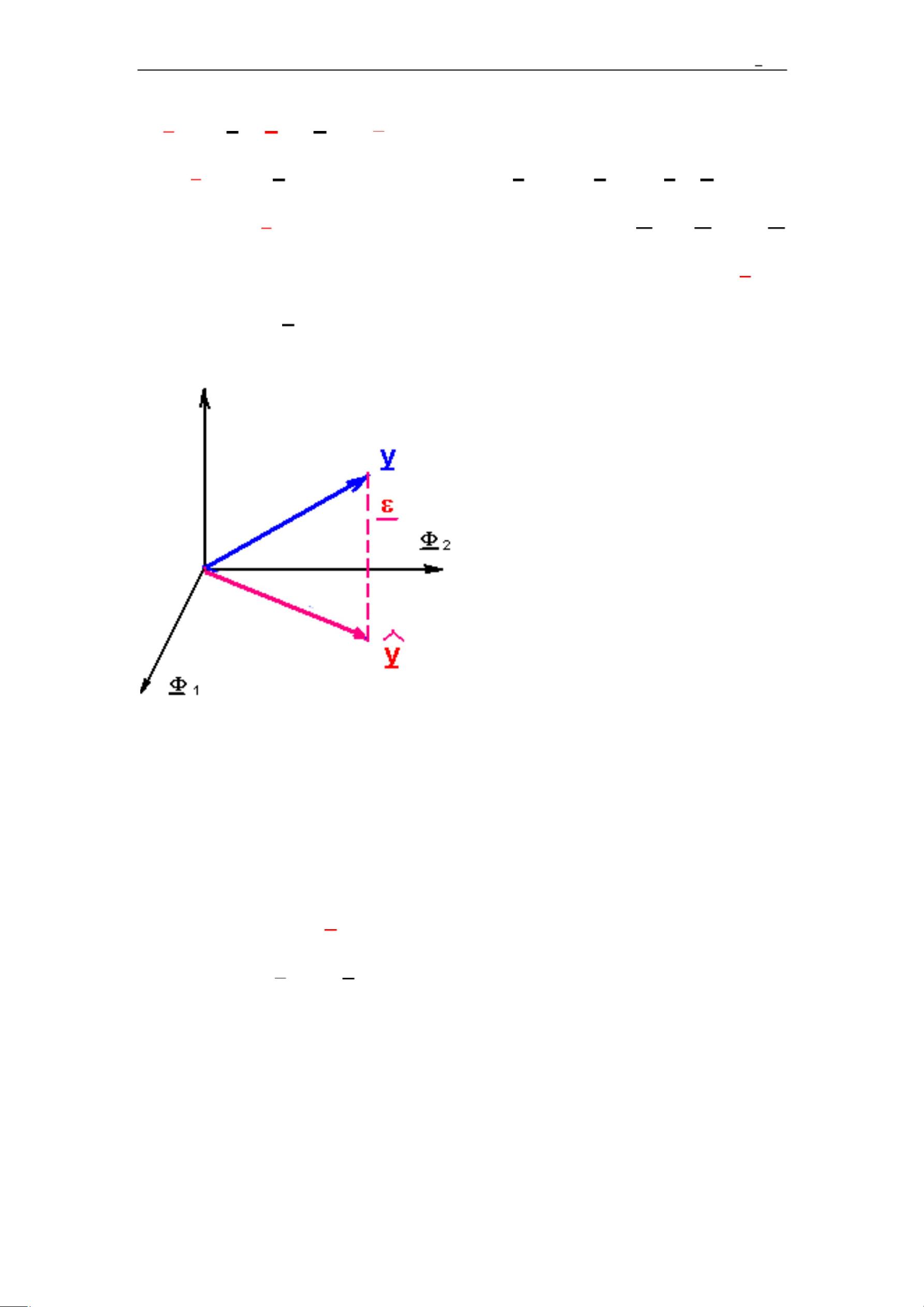
动态过程数学模型参数估计的最小二乘方法是统计学和信号处理中常用的一种技术，尤其在互联网数据分析和预测中有着广泛的应用。最小二乘法旨在找到一组参数，使得实际观测值与模型预测值之间的差异（残差）的平方和最小。 在描述的背景下，我们关注的是动态过程的静态线性模型参数估计。例如，一个简单的线性模型可以表示为 \( y = ax + \epsilon \)，其中 \( y \) 是观测变量，\( x \) 是输入变量，\( a \) 是未知参数，而 \( \epsilon \) 表示不可观测的随机误差项。通过多次实验，我们可以收集到多组 \( x \) 和对应的 \( y \) 值，目标是估计未知参数 \( a \)。 最小二乘估计的目标是找到一个参数值 \( a \) 使得残差平方和 \( J = \sum_{k=1}^{N}(y_k - ax_k)^2 \) 最小。通过对 \( J \) 关于 \( a \) 求导并令其等于零，可以得到最小化 \( J \) 的 \( a \) 值，即最小二乘估计 \( a^* \)。这种方法最早由高斯在1792年提出。 对于更复杂的多元线性回归模型 \( y = a_0 + a_1x_1 + a_2x_2 + ... + a_nx_n + \epsilon \)，我们可以将所有参数打包成一个向量 \( \theta = [a_0, a_1, ..., a_n] \)，并将输入向量 \( x \) 也表示为包含常数项1的向量 \( \phi \)。这样，模型可以写成 \( y = \phi\theta + \epsilon \)。通过矩阵形式表示，我们有 \( y = \Phi\theta + \epsilon \)，其中 \( \Phi \) 是输入数据的矩阵，\( y \) 和 \( \epsilon \) 分别是观测输出和误差向量。 最小二乘估计的求解可以通过矩阵运算实现。令 \( J \) 对 \( \theta \) 的偏导数等于零，我们可以解出参数估计向量 \( \theta \)： \[ \theta_{LS} = (\Phi^T\Phi)^{-1}\Phi^Ty \] 这个估计向量 \( \theta_{LS} \) 解了所谓的正规方程，它是最小化残差平方和的解。最小二乘估计有以下优良性质： 1. 线性性：\( \theta_{LS} \) 是 \( y \) 的线性函数。 2. 无偏性：期望值 \( E[\theta_{LS}] = \theta \)，即参数最小二乘估计是无偏的。 3. 最小方差性：\( \theta_{LS} \) 的估计误差协方差阵 \( \sigma^2(\Phi^T\Phi)^{-1} \) 达到了最小，其中 \( \sigma^2 \) 是误差项 \( \epsilon \) 的方差。 当误差项 \( \epsilon \) 是正态分布的零均值白噪声时，这些性质都成立。如果误差项是有色噪声，最小二乘估计可能就不再具有这些理想性质。 最小二乘法是一种实用且有效的工具，用于估计动态过程中的数学模型参数。它通过最小化预测值与实际观测值的偏差来寻找最佳参数，广泛应用于数据分析、控制工程和机器学习等领域。在互联网数据分析中，这种技术可以用来优化推荐系统、预测用户行为、识别网络流量模式等。