Matlab线性回归(拟合) (2).pdf

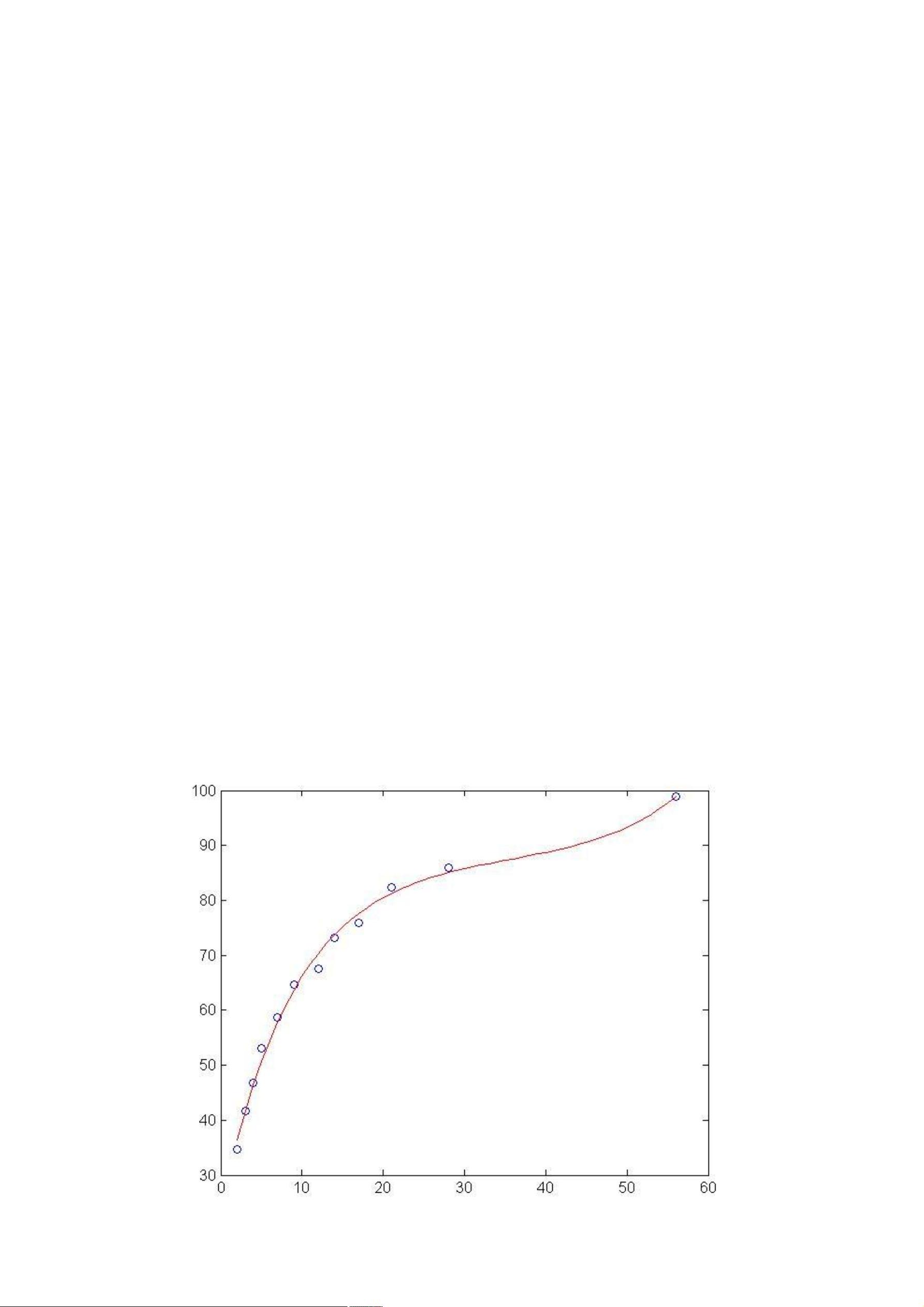
Matlab 是一种强大的数值计算和数据可视化软件，广泛应用于科学研究和工程领域。在处理数据分析时，线性回归是一种常用的方法，用于研究两个或多个变量之间的线性关系。本篇文章将详细探讨如何在 Matlab 中实现线性回归分析，包括多元线性回归、三次样条插值以及非线性拟合。 **一、多元线性回归** 多元线性回归是研究多个自变量（x1, x2, ..., xp）与一个因变量（y）之间关系的统计模型。在数学表达式中，模型通常表示为： y = β0 + β1x1 + ... + βpxp + e 其中，β0 是截距项，β1, β2, ..., βp 分别是各自变量的系数，e 表示误差项。Matlab 提供了 `regress` 函数来执行多元线性回归分析。使用方法如下： ```matlab [b, bint, r, rint, stats] = regress(y, x) ``` - `b` 是回归系数的估计值。 - `bint` 是回归系数的 95% 置信区间。 - `r` 是残差向量。 - `rint` 是每个残差的 95% 置信区间。 - `stats` 包含 R² 统计量、F 统计量及其临界概率 p。 通过检查 `bint`，我们可以判断每个自变量是否显著影响因变量。如果某个 βi 的置信区间不包含 0，则该自变量对模型的影响被认为是显著的。 **二、三次样条插值** 三次样条插值是一种光滑插值方法，常用于数据点间的平滑插值。在 Matlab 中，可以使用 `spline` 函数进行三次样条插值。例如： ```matlab x = 0:10; y = sin(x); xx = 0:.25:10; yy = spline(x,y,xx); plot(x,y,'o',xx,yy) ``` 这段代码首先定义了插值点 `x` 和 `y`，然后在更细的网格 `xx` 上进行插值并绘制结果。 **三、非线性拟合** Matlab 提供了 `nlinfit` 和 `lsqcurvefit` 函数来处理非线性拟合问题。这两个函数都需要用户提供目标函数模型和初始参数估计。例如： ```matlab beta = nlinfit(X, y, fun, beta0) x = lsqcurvefit(fun, x0, xdata, ydata) ``` - `nlinfit` 的输出 `beta` 是拟合后的系数，`r` 是残差，`J` 是雅可比矩阵。 - `lsqcurvefit` 的输出 `x` 是拟合结果，即目标函数的系数。 在实际应用中，用户需要编写一个 M 文件来定义非线性模型。例如，对于一个多元非线性模型 `y = a + b*x2 + c*x3 + d*x2^2 + e*x3^2`，可以在 M 文件 `myfun.m` 中定义如下： ```matlab function yy = myfun(beta, x) x1 = x(:,1); x2 = x(:,2); x3 = x(:,3); yy = beta(1) + beta(2)*x2 + beta(3)*x3 + beta(4)*x2.^2 + beta(5)*x3.^2; ``` 然后使用 `nlinfit` 进行拟合： ```matlab x = [x1, x2, x3]'; % 将数据组合为列向量 y = [y_data]'; beta0 = [1, 1, 1, 1, 1]'; [beta, r, J] = nlinfit(x, y, @myfun, beta0); ``` 总结起来，Matlab 提供了全面的工具来处理各种类型的回归和拟合问题，无论是简单的线性回归还是复杂的非线性模型，都可以通过内置函数方便地进行分析和建模。通过这些工具，研究人员和工程师能够更好地理解和预测数据之间的关系，从而做出更准确的决策。