Matlab线性回归(拟合) (2).docx

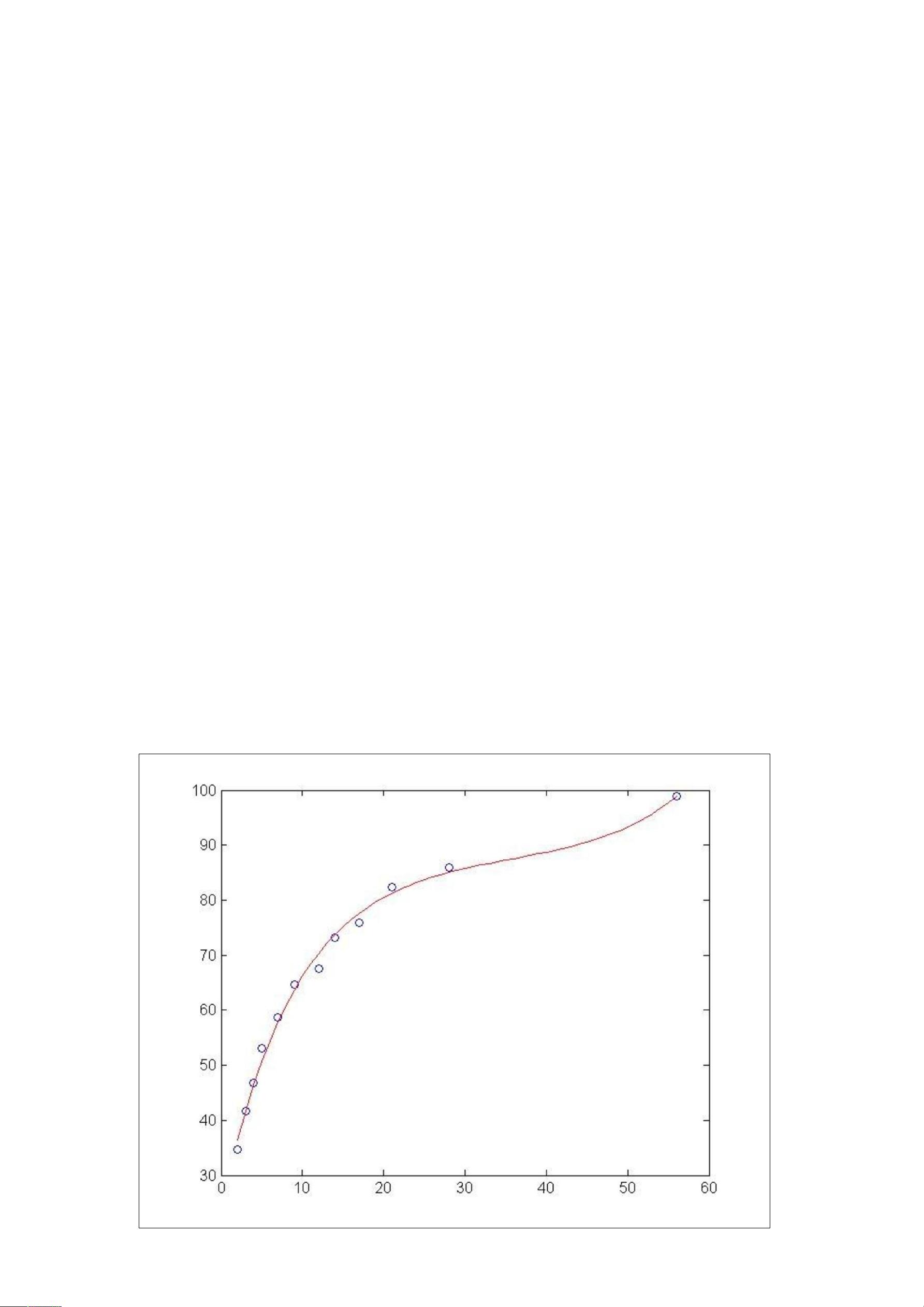
Matlab 是一种强大的数值计算和数据可视化工具，广泛应用于科学研究和工程领域。在统计建模中，线性回归是一种常用的方法，用于分析两个或多个变量之间的关系。在Matlab中，执行线性回归分析可以非常方便，特别是对于多元线性回归模型。 线性回归模型的基本形式是： \[ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_px_p + \epsilon \] 其中，\( y \) 是响应变量，\( x_1, x_2, \ldots, x_p \) 是解释变量，\( \beta_0, \beta_1, \ldots, \beta_p \) 是待估计的参数，\( \epsilon \) 表示随机误差项。在Matlab中，可以使用 `regress` 函数来估计这些参数。例如，`b = regress(y, x)` 会返回一个向量 `b`，其中包含了 \( \beta \) 的估计值。如果需要计算残差、置信区间等其他统计量，可以使用更完整的调用形式，如 `[b, bint, r, rint, stats] = regress(y, x)`。 对于非线性拟合，Matlab 提供了 `nlinfit` 函数。非线性拟合的模型通常由用户定义，通过一个 M-File 或内联函数来描述。例如，如果模型是 \( y = a + bx^2 + cx^3 \)，可以创建一个 M-File `model.m` 来表示这个函数，然后用 `nlinfit` 进行拟合。在实际操作中，还需要提供初始参数估计值 `beta0` 和输入数据 `x` 和 `y`。 在给定的例子中，有这样一个非线性模型： \[ y = a + bx_2 + cx_3 + dx_2^2 + ex_3^2 \] 通过编写 M-File 并使用 `nlinfit` 函数，可以找到参数 \( a, b, c, d, e \) 的估计值。具体步骤包括编写 M-File 来定义函数模型，然后在主程序中调用 `nlinfit`，传入相应的数据和初始估计值。 除了这些基础的线性和非线性拟合功能，Matlab 还提供了丰富的数据分析和可视化工具，比如绘制残差图、预测曲线等，以便于理解和验证模型的适用性。通过熟练掌握这些工具，可以有效地进行各种复杂的数据建模任务。 Matlab 提供的线性回归和非线性拟合功能强大且灵活，适合处理各种统计建模问题。无论是简单的线性关系还是复杂的非线性关系，都可以通过适当的方法在Matlab中实现建模和分析。对于互联网领域的数据分析，这种灵活性和强大功能尤其重要，能够帮助研究人员快速地探索数据、建立模型并作出决策。