
近场天线测量 课程实验报告
学院 班
姓名 学号
电话
实验日期 2024 年 1 月 1 日
导师
任课老师
成 绩
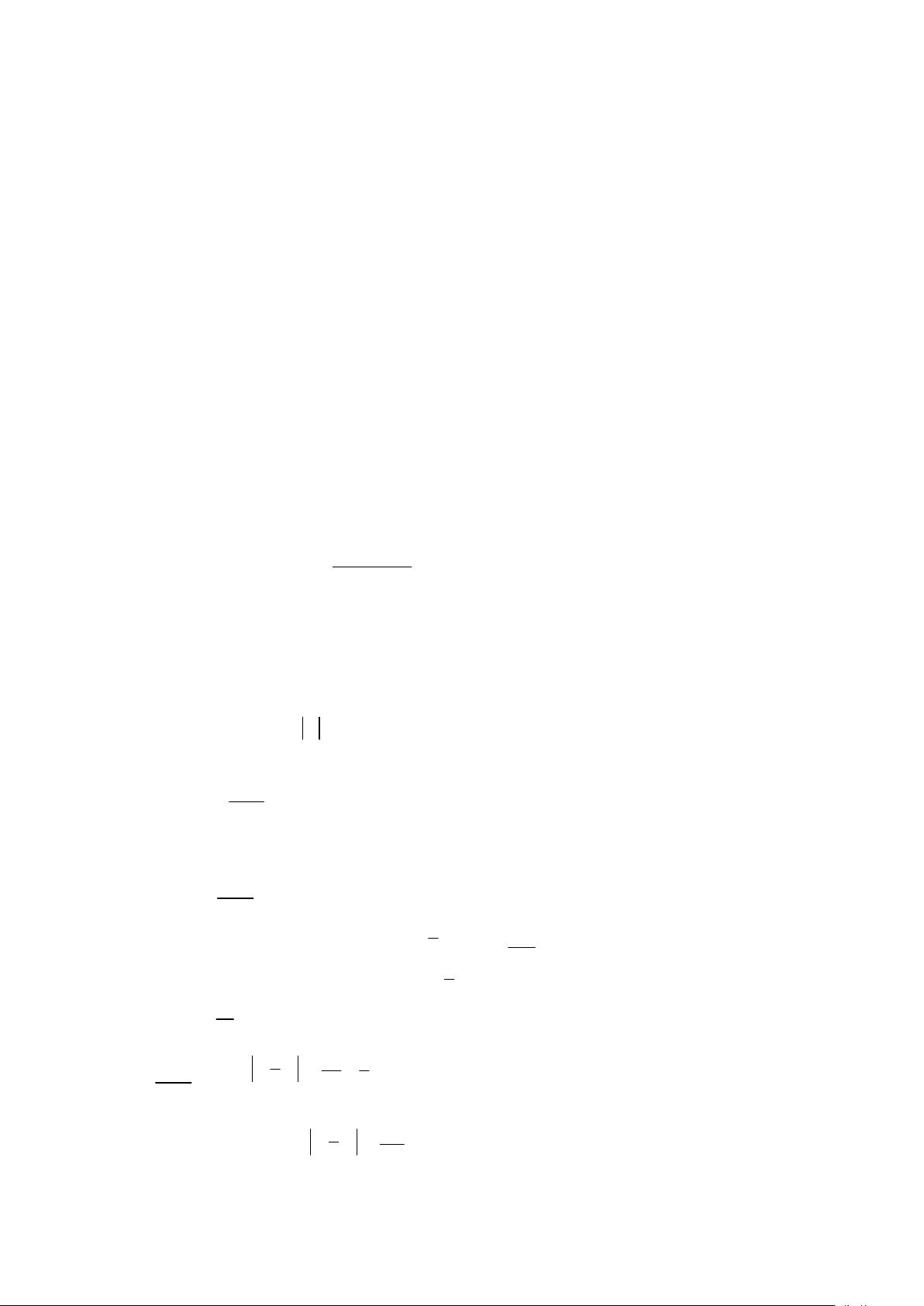
一、实验目的
本实验主要研究:1、计算机中快速傅里叶算法与直接求和的区别,并对两者
结果与理论结果进行比较,并探讨两者在计算机实现过程中的时间复杂度;2、利
用一维驻相法推导天线远场方向图函数与柱面波谱
( )
n
a h
、
( )
n
b h
的关系式,深刻
理解驻相法、天线方向函数、柱面波图;3、计算角锥喇叭的理论 E 面和 H 面归一
化远场方向图并与实测结果进行比较。
二、实验原理
1、 实验一
已知
| |
( )
x
f x e
-
=
,求
| | 2
( )
x j x
F e e dx
¥ pw
¥
w
- -
-
= ò
。
其理论结果为
( )
2
2
( )
1 2
F
w
pw
=
+
。
当
| |
w
很大时,
( ) 0F
w
»
。
取
Ω 100
w
= =
时,
5
( ) 10 0F
w
-
< »
。
故可近似认为当
Ω
w
>
时,
( ) 0F
w
»
,即可以近似认为
( )
f x
是一个谱宽有限
的含水,带限为
2W
。
取
0.005
2
x
p
p
D £ =
W
,则由取样定理有
| Δ | 2 Δ
( ) Δ
m x j m x
m
F e e x
¥
pw
¥
w
- - ×
=-
= å
令
Δ
n
N x
w
=
,则有
1
2
2
| Δ |
2
( ) Δ
N
mn
j
m x
N
N
m
F e e x
p
w
-
-
=-
» å
令
2
N
m k+ =
,则有:
2
1
( )Δ
( )
2
2
0
( ) Δ
Δ
N
n N
N
k x
j k
N
k
n
F e e x
N x
p
-
- -
- -
=
» å
2
1
( )Δ
2
0
( 1) Δ
N
kn
N
k x
j
n
N
k
xe e
p
-
- -
-
=
= - å

2
1
0
( 1) ( 0,1, , 1)
kn
N
j
n
N
k
k
f e n N
p
-
-
=
= - å = -L
其中
( )Δ
2
( )Δ
2
Δ 0,1, , 1
2
Δ , , 1
2
N
k x
k
N
k x
N
xe k
f
N
xe k N
-
ì
= -
ï
ï
=
í
ï
= -
ï
î
L
L
取
2048N =
,则
Δ 1024 0.005 5
2
N
x = × »
,故有
Δ
2
1
N
x
e
-
<<
。
2、 实验二
利用一维驻相法推导天线远场方向图函数与柱面波谱
( )
n
a h
、
( )
n
b h
的关系式。
具体推导如下:
(4) (4)
, ,
( ) ( ) ( ) ( )
n n h n n h
n
E a h M r b h N r dh
¥
¥
¥
¥
-
=-
é ù
= å ò +
ë û
(4) (4)
, ,
( ) ( ) ( ) ( )
n n h n n h
n
R
H a h N r b h M r dh
j m
¥
¥
¥
¥
w
-
=-
é ù
= å ò - +
ë û
其中
(4) (2) 2
,
( ) (
ˆ
)
ˆ
( )
jn jhz
n h n n
jn
M r H H e e
¢ j
r r r j
r
-
é ù
= Ù - Ù Ù
ê ú
ë û
2
(4) (2) 2 2
,
( ) ( ) ( ) ( )
ˆ ˆ
ˆ
jn ji
n h n n n
jh nh
N r H H H z e e
k k
¢ j t
r r r j r
r r
-
é ù
Ù
= - Ù Ù + Ù Ù + Ù
ê ú
ë û
r
下面求天线远场的方向函数与
( )
n
a h
、
( )
n
b h
的关系:
sinr
r q
=
其中当
r
¥
®
时,
r ¥
®
。
此时有
1
2
(2)
4
2
( , )
j
n j
n
H j e e
p
r
r
p r
- Ù
æ ö
Ù =
ç ÷
Ù
è ø
1
2
(2)
4
2
( , )
j
n j
n
H j e e
p
¢ r
r
p r
-
- Ù
æ ö
Ù =
ç ÷
Ù
è ø
将
(4)
,
( )
n h
M r
r
r
划分为两项:

(2)
( )
jn jhz
n
jn
M H e e
j
r
r
r
-
= Ù
(2)
( )
jn jhz
n
M H e e
¢ j
j
r
-
= Ù
令
(4)
1 ,
( [
ˆ ˆ
) ( ) ]
n n h n n
n n
E a h M r dh a M a M dh
¥ ¥
¥ ¥
¥ ¥ r j
¥ ¥
r j
- -
=- =-
= å ò = å ò +
1
( )
4 2
2
( )
j
n jn j hz
n n
n n
jn
I a M dh a j e e e dh
p
¥ ¥
¥ ¥ j r
¥ r ¥
¥ ¥
r p r
- Ù +
- -
=- =-
= å ò = å ò
Ù
又因为
sinr
r q
=
cosz r
q
=
2 2
k hÙ = -
所以
1
( sin cos )
4 2
2
( )
sin
j
n jn jr h
n
n
jn
I a j e e e dh
r
p
¥
¥ j q q
¥
¥
q p r
- Ù +
-
=-
= å ò
Ù
令
1
4 2
2
( ) ( )
sin
j
n jn
n
jn
f h a j e e
r
p
j
q p r
=
Ù
2 2
( ) sin cos sin cosg h h k h h
q q q q
= Ù + = - +
令
0
0
2 2
0
( ) sin cos 0
h
g h h
k h
q q
-
= + =
-
¢
,解得
0
cosh k
q
=
。
又因为
0
2
1
( )
sin
g h
k
q
= -
¢¢
,
0
( )g h k=
。
由一维驻相法可知
[ ]
0 0
( ) sgn ( )
( )
4
0
0
2
( ) ( )
( )
j rg g
b jrg d
a
I f e f e
r g
p
a a
a a
p
a a
a
ì ü
- +
í ý
-
î þ
¢¢
= ò
¢¢
=
+
所以
[ ]
0 0
( ) sgn ( )
4
0
0
2
( )
( )
j rg g
n
I f h e
r g h
p
¥
a a
¥
p
é ù
- +
ê ú
ë û
=-
¢¢
= å
¢
+
¢
其中
4
0
2
2
( ) ( cos )
sin sin
j
n jn
n
jn
f h a k j e e
r rR
p
j
q
q p q
=
。
由
0
2
1
( )
sin
g h
k
q
= -
¢¢
、
4
0
2
2
( ) ( cos )
sin sin
j
n jn
n
jn
f h a k j e e
r rR
p
j
q
q p q
=
代 入

[ ]
0 0
( ) sgn ( )
4
0
0
2
( )
( )
j rg g
n
I f h e
r g h
p
¥
a a
¥
p
é ù
- +
ê ú
ë û
=-
¢¢
= å
¢
+
¢
,最后化简可得
( 2)
2
2
sin
n
jkr jn
n
n
nj
I a e e
r
¥
j
¥
q
+
-
=-
= å
由对称性可得
0I =
。
令
Π
n
n
a M dh
¥
¥
¥ j
¥
-
=-
= å ò
,解得
1
( sin cos )
4 2
2
( cos ) ( )
j
n jn jr h
n
n
a k j e e e dh
p
¥
¥ j q q
¥
¥
q
p r
-
- Ù +
-
=-
é ù
Õ = å ò Ù
ê ú
Ù
ë û
利用一维驻相法可得:
2
( )
4 4
2
2 2 sin
Π ( cos ) sin
sin
j
j k
n jn
n
k
a k k j e e e
rk r
p p
t
j
p q
q q
p q
-
- -
= å ×
2 sin
( cos )
ˆ
jkr n jn
n
n
k
e j e a k
r
¥
j
¥
q
q
-
=-
= - å φ
所以
µ
1
2 sin
I Π ( cos
ˆ ˆ
)
jkr n jn
n
n
k
E e j e a k
r
¥
j
¥
q
r j q j
-
=-
= + = - å
。
令
(4)
2 ,
( ) (
ˆ
)
ˆ ˆ
n n h n n n z
n n
E b h N r dh b N b N b N z dh
¥ ¥
¥ ¥
¥ ¥ r j
¥ ¥
r j
- -
=- =-
é ù
= å ò = å ò + +
ë û
,
令
1
2 4
2
I ( )
j
n j jn jh
n n
n
jh
b N dh b j e e e e dh
k
p
¥ ¥
¥ r j v
¥ r
¥ ¥
p r
-
- Ù -
-
=- -
= å ò = å × Ù
Ù
。
利用一维驻相法可得:
2
( 1) 2
4 4
2
2 sin 2
I sin cos
sin
j j
n jn jk
n
n
b
k
j e e k e e
k r rk
p p
¥
j t
¥
p q
q q
p q
-
+ -
=-
= å - ×
( 1)
2 sin cos
( cos )
jkr n jn
n
n
k
e j e b k
r
¥
j
¥
q q
q
- +
=-
= - å
令
Π III
n n z
n n
b N dh b N dh
¥ ¥
¥ ¥
¥ j ¥
¥ ¥
- -
=- =-
= å ò = å ò
,利用一维驻相法可得:
( 1)
cot
jkr n jn
n
nb
e j e
k
¥
j
¥
q
- +
-
Õ = å
由对称性可知
Π 0=
2
2k sin
Ш= j ( cos )
jk n jn
n
n
e j e b k
r
¥
j
¥
q
q
-
=
å
所以
2
sin
2
2 sin cos 2 sin
ˆ ˆ ˆ
ˆ
ˆ
Шz
jkr n
n
n
k k
E jb e j e z
r r
j
q q q
r j r
¥
-
=-¥
é ù
= I + P + = - +
ê ú
ë û
å
又因为
ˆ
cos si
ˆ
n
ˆ
z
q r q q
= -

















