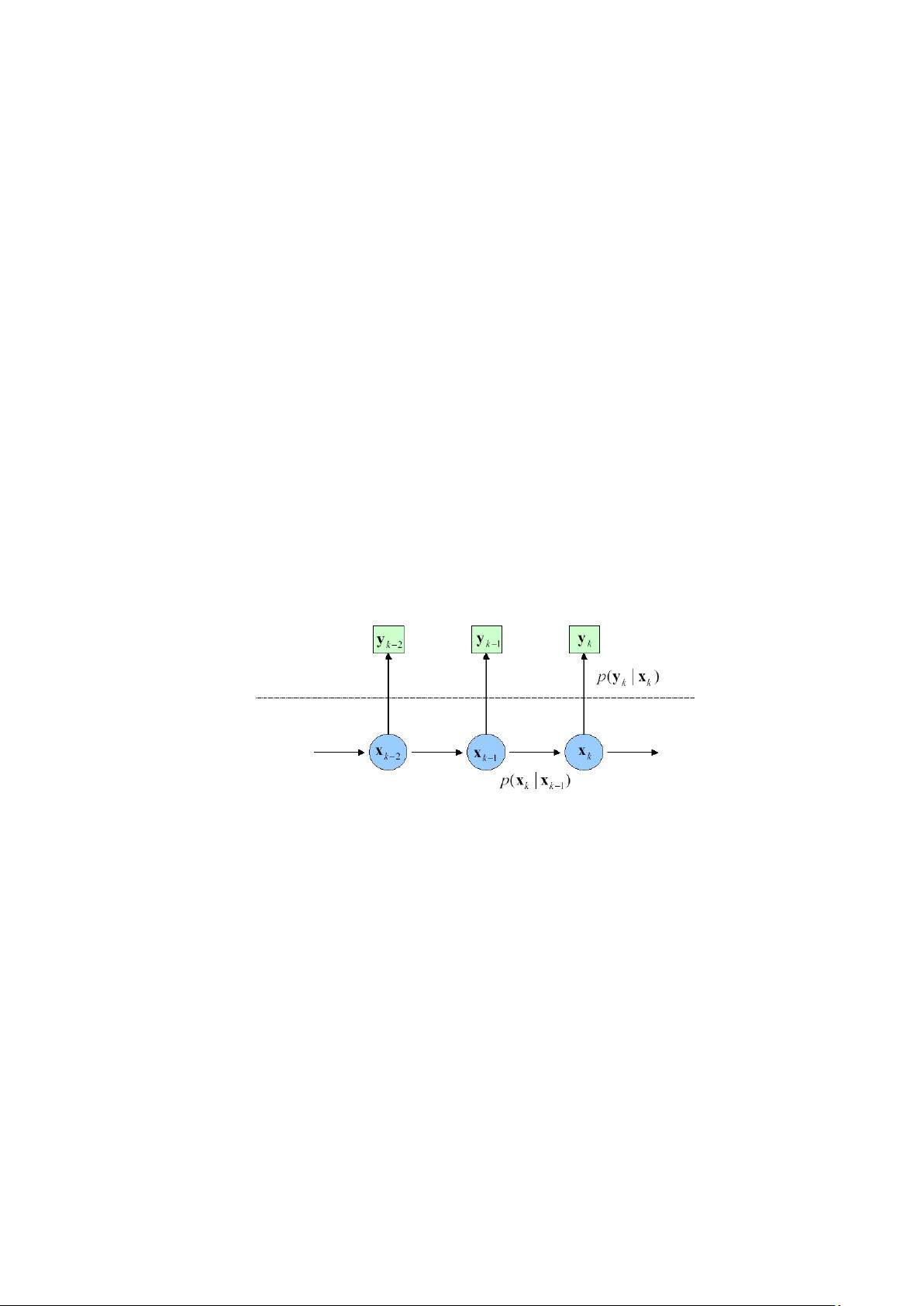
【老生谈算法】matlab实现粒子滤波及实现.doc

【老生谈算法】matlab实现粒子滤波是关于如何使用MATLAB编程语言来实施粒子滤波算法的一个详细讲解。粒子滤波是一种非参数化的概率方法，主要用于解决非线性、非高斯系统的状态估计问题。它基于递推贝叶斯滤波理论，通过在状态空间中使用一组随机样本（粒子）来近似表示复杂的概率密度函数。 在贝叶斯滤波框架下，粒子滤波的核心思想是通过蒙特卡洛模拟来追踪系统状态的概率分布。在目标跟踪问题中，系统状态由状态转移方程和观测方程描述，其中状态转移方程描述了状态从一个时间步到下一个时间步的演变，观测方程则关联了观测值与状态之间的关系。粒子滤波器利用一阶马尔可夫模型假设，即当前状态只依赖于上一状态，并假设观测值独立于历史状态，仅与当前状态相关。 粒子滤波算法包括两个主要步骤：预测和更新。预测阶段，根据上一时刻的粒子分布和状态转移模型生成下一时刻的先验概率分布；更新阶段，利用新的观测数据对先验概率分布进行修正，得到后验概率分布。这个过程可以理解为在状态空间中重新分配粒子权重，以更准确地反映实际状态的分布。 MATLAB实现粒子滤波时，通常涉及以下关键步骤： 1. 初始化：生成一组初始粒子，每个粒子代表系统状态的一种可能情况，并赋予相等的权重。 2. 预测：应用状态转移方程更新每个粒子的位置，形成新的粒子分布。 3. 重采样：根据粒子的权重进行重采样，保留高权重的粒子，减少低权重粒子的影响，防止粒子退化（即所有粒子都聚集在一个或少数几个状态上）。 4. 更新：使用观测模型计算每个粒子的观测值，并根据观测数据调整粒子的权重。 5. 重复预测和更新步骤，直到达到预定的迭代次数或满足停止条件。 粒子滤波相对于其他非线性滤波器（如扩展卡尔曼滤波和无迹卡尔曼滤波）的一大优势在于其对非线性模型和复杂概率分布的适应性。尽管粒子滤波的计算量较大，但通过优化采样策略（如重要性采样）和有效粒子数量，可以提高算法效率并获得接近最优的估计结果。 在MATLAB中实现粒子滤波时，可以利用MATLAB的内置函数和工具箱，如统计和机器学习工具箱中的函数，或者自定义代码来创建特定的粒子滤波算法。需要注意的是，理解和优化粒子滤波器的性能通常需要对概率论、统计学和数值方法有深入的理解。 MATLAB实现粒子滤波是解决非线性动态系统状态估计问题的有效手段，它结合了贝叶斯滤波理论和蒙特卡洛模拟，为复杂问题提供了灵活且直观的解决方案。通过熟练掌握这一技术，工程师们能够在目标跟踪、信号处理和自动控制等领域实现高精度的系统状态估计。