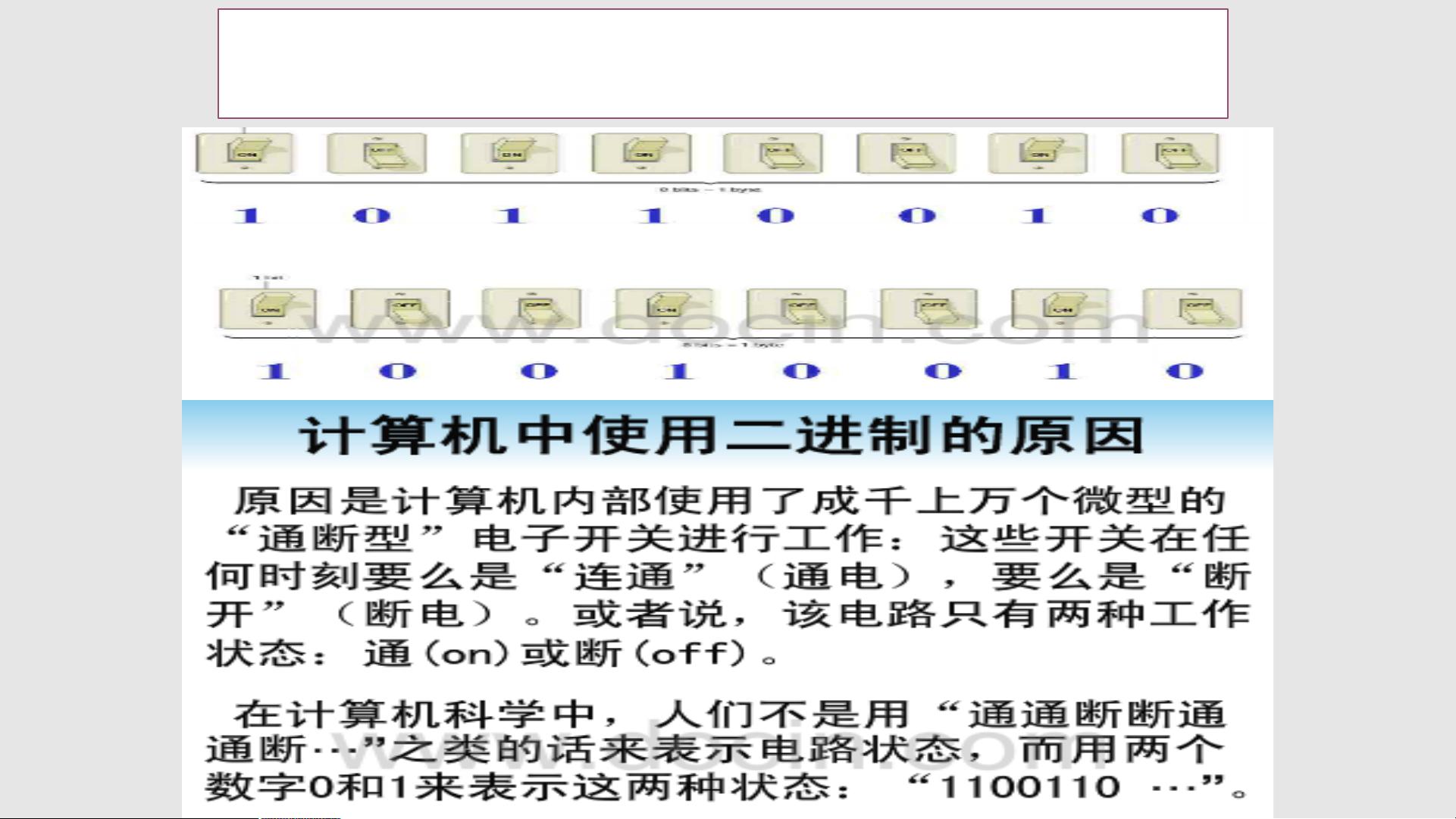
进位计数制，简称进制，是计算机科学中用于表示数值的基本方式。常见的进制有二进制、八进制、十进制和十六进制。每种进制都有其特定的基数和数字符号。
1. **基数**：基数指的是一个数制中所使用的数字符号的个数。例如，十进制的基数是10，包含数字0到9；二进制的基数是2，只包含0和1。
2. **位权**：位权是指在数制中每个位置的数值权重，与基数的关系是基数的整数次幂。例如，在十进制中，个位的位权是10^0=1，十位的位权是10^1=10，百位的位权是10^2=100。
3. **进位规则**：进位制的进位规则决定了数值的增涨方式，如逢十进一，逢二进一等。比如在二进制中，当某一位上的数值达到2时，就会进位到高一位。
4. **数制表示法**：数制通常通过在数字后加上特定的字母来表示，如二进制用B（Binary），八进制用Q（Octal），十六进制用H（Hexadecimal）。例如，二进制数11011.11可以表示为(11011.11)2或11011.11B。
5. **数制转换**：在计算机处理数据时，通常会将用户输入的十进制数转换为二进制，处理后再转换回十进制进行输出。数制之间的转换可以通过位权展开和求和完成。例如，十进制数923.45可以转换为二进制数1101.11*2^3+1*2^2+0*2^1+1*2^0+1*2^-1+5*2^-2，计算出相应的二进制表示。
6. **运算规则**：不同进制的数进行运算时，需要先转换为同一进制，然后按照该进制的运算法则进行计算。例如，二进制数1101和1011相加，需要先转换为十进制进行加法运算，然后再转换回二进制。
7. **实际应用**：生活中，进制无处不在，例如一天有24小时（二进制表示），一小时60分钟（六十分进制），一年12个月（十二进制）等。
掌握进制转换和运算对于理解计算机的基础工作原理至关重要，因为计算机内部是以二进制的形式存储和处理信息的。在编程、硬件设计和数据分析等领域，都需要频繁进行不同进制间的转换。了解这些基础知识，能帮助我们更好地理解和解决与计算机相关的各种问题。
VIP享7折，此内容立减5.97元 
