decade of nineties in 20th century [10]. And now the
refraction method has been successfully applied on an
aircraft with high altitude of 30 km [11]. As a promising
method, it has attracted many researchers so far.
In previous works, the stellar refraction program uses
two star sensors. The first one observes the stars that
never forms refraction, the other observes the refraction
stars. Then the refraction star can be identified according
to the differences between the refraction star and normal
star. Actually, only one star sensor can achieve the above
goal. The extra sensor will increase the design cost and
burden the initial alignment process. In view of this
situation, this paper presents an autonomous satellite
navigation scheme based on stellar refraction with single
star sensor. The installed angle of star sensor determines
the number of observed refraction stars in a satellite orbit
period, which affects the accuracy of the navigation. In this
paper, a method on the basis of the principle of spherical
geometry is presented to calculate the optimal installed
angle. Moreover, the refraction star identification method
uses only one star sensor is also given. Finally, a simulation
is utilized to verify the feasibility of the proposed scheme.
2. Principle of stellar refraction
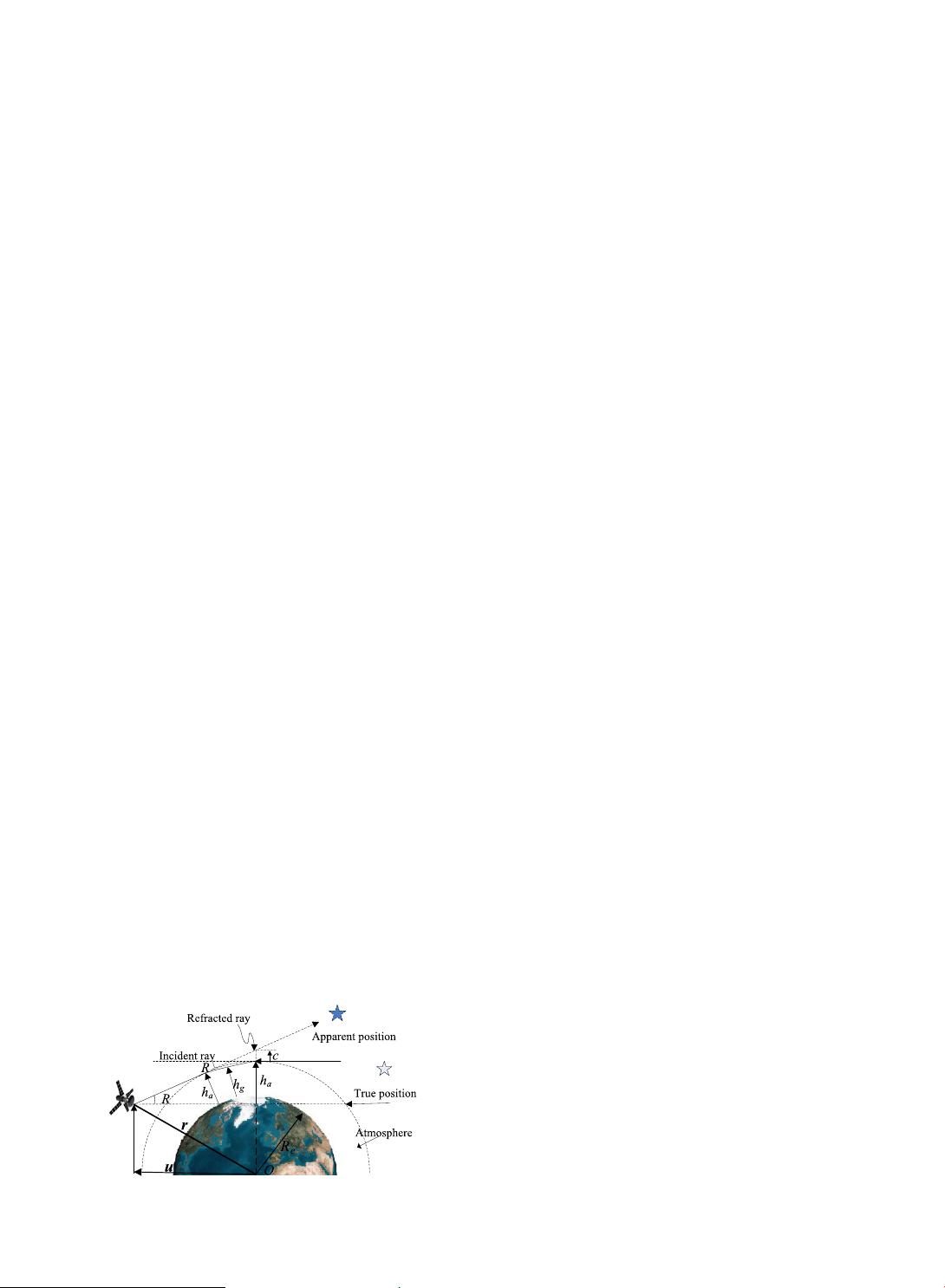
When starlight passes through the Earth's atmosphere,
it will be refracted and bent inward. Viewed from the
satellite, the apparent position of star will be higher than
the actual one. The refracted rays appear to gaze at the
horizon at an apparent height h
a
but actually graze the
horizon at a slightly lower height h
g
. The angle R between
the incident ray and refracted ray is the starlight refraction
angle (see Fig. 1).
From the geometric relationship shown in Fig. 1, the
following equation can be derrived
h
a
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
u
2
p
þu tan RR
e
c ð1Þ
where
r ¼jrj¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x
2
þy
2
þz
2
p
u ¼jr U uj¼jxs
x
þys
y
þzs
z
j
(
ð2Þ
r ¼½
xyz
is the position vector from Earth's core to
satellite, u ¼½
s
x
s
y
s
z
T
is the starlight vector before
refraction which can be obtained from the star catalog
after the star is identified, R
e
is the Earth radius and c is
very small and can be ignored.
According to the atmospheric refraction model we can
also obtain the relationship between h
a
and R. The
development of autonomous navigation based on stellar
refraction result in a lot of interest in the study of the
atmospheric refraction model [12–14]. Where, the litera-
ture [12] improved the observation model. Compared with
the existing model, it establishes an continuous range of
altitudes (CRA) from 20 km to 50 km on the basis of the
data provided by U.S. Standard Atmosphere
h
a
¼ h
g
þkðλÞρðR
e
þh
g
Þ
h
g
¼ 57:0816:441 lnðRÞ
ρ ¼ 1:762expð0:152h
g
Þ
8
>
<
>
:
ð3Þ
where h
a
is the apparent ray altitude; λ ¼ 0:7 μm is the
wavelength of starlight; kðλÞ¼2:2517 10
7
is the scat-
tering parameter; h
g
is the tangent height; R is starlight
refraction angle, R and h
g
are measured in second (″)
and km respectively; ρ is the atmospheric density and
its unit is kg=m
3
. Because R
e
⪢h
g
and kðλÞρo 2 10
3
for
the atmosphere altitude higher than 20 km [15],so
h
ac
h
g
þkðλÞρR
e
, then the relationship between h
a
and R
can be derrived as follows
h
a
¼ 57:081þ2:531exp½0:981 lnðRÞ8:6896:441 ln ðRÞ
ð4Þ
where h
a
is measured in kilometer. If the starlight
refraction angle R can be obtained, the apparent height
h
a
can be calculated by (4). According to (1), h
a
is a
function of position. so, if we let h
a
as the measurement
data, the satellite's position and velocity can be calculated
by combining the dynamics equation of orbits and using
the reasonable filtering algorithm.
3. Scheme design
3.1. Workflow of the new scheme
The star sensor is used to observe the refraction star
and the normal star. Its optical axis is installed on the
satellite's orbit plane. In general, to calculate the refraction
angle and to identify the refraction star require two star
sensors as shown in Fig. 2. Star sensor A observes the
normal star, and then outputs the satellite's attitude and
its optic axis's direction after the star identification pro-
cess. According to the installation matrix between A and B,
the direction of B star sensor's optic axis can be obtained.
We choose the stars fall into Field of View (FOV) of B
from the star catalog, henceforth generating a simulated
star image. Using this star image and the actual one can
identify the refraction star. Then the refraction angle can
be calculated.
As a matter of fact, both the refraction stars and the
normal stars exist in the image captured by sensor B. If the
traditional star identification method is utilized to deal
with this star image, only the normal stars can be
identified successfully. The rest is the refraction star.
If the number of the normal stars is larger than 3, we
can still successfully identify these stars. It means that we
can also obtain the satellite's attitude and the direction of
sensor's optic axis. Utilizing the differences between the
refraction star and the normal stars can identify the
refraction star and calculate the refraction angle. Finally,
Fig. 1. Geometric illustration of stellar atmospheric refraction.
H.-m. Qian et al. / Acta Astronautica 96 (2014) 45–5246
评论0
最新资源