EPnP-AnAccurateO(n)SolutiontothePnPProblem.pdf_pnp位姿估计matlab工具包资源-CSDN文库

需积分: 44 63 浏览量 2020-08-08 07:28:14 上传评论收藏 2.3MB PDF 举报

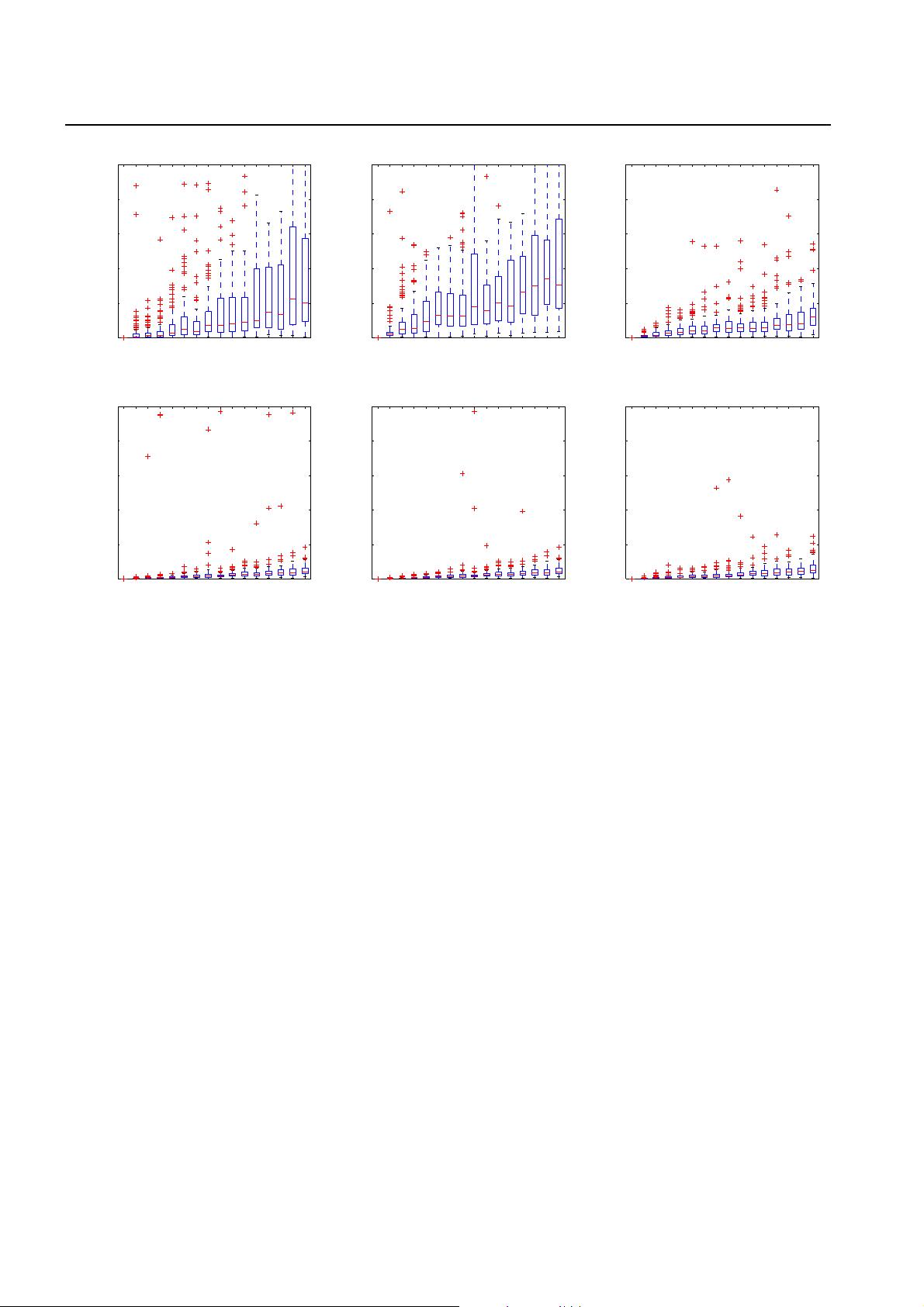
EPnP- An Accurate O(n) Solution to the PnP Problem.pdf EPnP是一种高效的perspective-n-Point（PnP）问题解决方案，该问题旨在从n个3D-2D点对应关系中估计已校准摄像机的姿态。传统的PnP问题解决方案的计算复杂度为O(n5)或O(n8)，而EPnP方法的计算复杂度仅为O(n)，且适用于n ≥ 4的情况，並且可以正确处理平面和非平面配置。 EPnP方法的核心思想是将n个3D点表达为四个虚拟控制点的加权和，于是问题简化为估计这些控制点在摄像机参考系中的坐标。通过将这些坐标表达为12 × 12矩阵的特征向量的加权和，并解一个小常数的二次方程，可以在O(n)时间内解决这个问题。如果需要最大精度，可以使用闭式解决方案的输出来初始化高斯-牛顿方案，以提高精度。 EPnP方法的优点在于，它可以快速地解决PnP问题，从而提高计算机视觉应用中的性能。此外，该方法还可以处理平面和非平面配置，并且可以在synthetic和real-data上进行测试。 EPnP方法的实现步骤可以概括为： 1. 将n个3D点表达为四个虚拟控制点的加权和； 2. 将控制点的坐标表达为12 × 12矩阵的特征向量的加权和； 3. 解一个小常数的二次方程以估计控制点的坐标； 4. 使用估计的控制点坐标来计算摄像机的姿态。 EPnP方法的优点是： * 高效：EPnP方法的计算复杂度为O(n)，远低于传统方法的O(n5)或O(n8)。 * 通用性：EPnP方法可以处理平面和非平面配置。 * 高精度：EPnP方法可以提供高精度的姿态估计结果。 EPnP方法的应用前景广泛，包括： * 计算机视觉：EPnP方法可以用于计算机视觉中的姿态估计、目标跟踪、场景重建等。 * 机器人视觉：EPnP方法可以用于机器人视觉中的姿态估计、目标检测、场景理解等。 * 增强现实：EPnP方法可以用于增强现实中的姿态估计、场景理解等。 EPnP方法是一种高效、通用、高精度的PnP问题解决方案，对计算机视觉和机器人视觉等领域具有重要的应用价值。

展开

资源推荐

资源详情

资源评论

Noname manuscript No.

(will be inserted by the editor)

EPnP: An Accurate O(n) Solution to the PnPProblem

Vincent Lepetit · Francesc Moreno-Noguer · Pascal Fua

Received: date / Accepted: date

Abstract We propose a non-iterative solution to the

PnP problem—the estimation of the pose of a cali-

brated camera from n 3D-to-2D point correspondences—

whose computational complexity grows linearly with n.

This is in contrast to state-of-the-art methods that are

O(n

) or even O(n

), without being more accurate. Our

method is applicable for all n ≥ 4 and handles properly

both planar and non-planar conﬁgurations. Our central

idea is to express the n 3D points as a weighted sum of

four virtual control points. The problem then reduces

to estimating the coordinates of these control points

in the camera referential, which can be done in O(n)

time by expressing these coordinates as weighted sum

of the eigenvectors of a 12 × 12 matrix and solving a

small constant number of quadratic equations to pick

the right weights. Furthermore, if maximal precision is

required, the output of the closed-form solution can be

used to initialize a Gauss-Newton scheme, which im-

V. Lepetit

Computer Vision Laboratory

École Polytechnique Fédérale de Lausanne (EPFL)

CH-1015 Lausanne, Switzerland

F. Moreno-Noguer (Corresponding author)

Computer Vision Laboratory

École Polytechnique Fédérale de Lausanne (EPFL)

CH-1015 Lausanne, Switzerland

Tel.: +41-216-931288

Fax: : +41-216-937520

E-mail: fmorenoguer@gmail.com

P. Fua

Computer Vision Laboratory

École Polytechnique Fédérale de Lausanne (EPFL)

CH-1015 Lausanne, Switzerland

proves accuracy with negligible amount of additional

time. The advantages of our method are demonstrated

by thorough testing on both synthetic and real-data.

Keywords Pose estimation · Perspective-n-Point ·

Absolute orientation

1 Introduction

The aim of the Perspective-n-Point problem—PnPin

short—is to determine the position and orientation of

a camera given its intrinsic parameters and a set of n

correspondences between 3D points and their 2D pro-

jections. It has many applications in Computer Vision,

Robotics, Augmented Reality and has received much

attention in both the Photogrammetry [21] and Com-

puter Vision [12] communities. In particular, applica-

tions such as feature point-based camera tracking [27,

18] require dealing with hundreds of noisy feature points

in real-time, which requires computationally eﬃcient

methods.

In this paper, we introduce a non-iterative solution

with better accuracy and much lower computational

complexity than non-iterative state-of-the-art methods,

and much faster than iterative ones with little loss of

accuracy. Our approach is O(n) for n ≥ 4 whereas all

other methods we know of are either specialized for

small ﬁxed values of n, very sensitive to noise, or much

slower. The specialized methods include those designed

to solve the P3P problem [9,24]. Among those that han-

dle arbitrary values of n [8,6,13,11,24,29,7,2,9], the

lowest-complexity one [7] is O(n

) but has been shown

The Matlab and C++ implementations of the algo-

rithm presented in this paper are available online at

http://cvlab.epfl.ch/software/EPnP/

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

Clamped DLT

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

EPnP

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

LHM

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

EPnP+LHM

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

100

rotation error (%)

Gaussian image noise (pixels)

EPnP+GN

Fig. 1 Comparing the accuracy of our method against state-of-the-art ones. We use the boxplot representation: The blue boxes

denote the ﬁrst and third quartiles of the errors, the lines extending from each end of the box depict the statistical extent of the data,

and the crosses indicate observations that fall out of it. Top r ow . Accuracy of non-iterative methods as a function of noise when using

n =63D-to-2D correspondences: AD is the method of Ansar and Daniilidis [2]; Clamped DLT is the DLT algorithm after clamping

the internal parameters with their known values; and EPnP is our method. Bottom row. Accuracy of iterative methods using n =6:

LHM is Lu et al.’s method [20] initialized with a weak perspective assumption; EPnP+LHM is Lu et al.’s algorithm initialized with

the output of our algorithm; EPnP+GN, our method followed by a Gauss-Newton optimization.

to be unstable for noisy 2D locations [2]. This is cur-

rently addressed by algorithms that are O(n

) [24] or

even O(n

) [2] for better accuracy whereas our O(n) ap-

proach achieves even better accuracy and reduced sen-

sitivity to noise, as depicted by Fig. 1 in the n =6case

and demonstrated for larger values of n in the result

section.

A natural alternative to non-iterative approaches

are iterative ones [19,5,14,17,20] that rely on mini-

mizing an appropriate criterion. They can deal with

arbitrary numbers of correspondences and achieve ex-

cellent precision when they converge properly. In par-

ticular, Lu et al. [20] introduced a very accurate algo-

rithm, which is fast in comparison with other iterative

ones but slow compared to non-iterative methods. As

shown in Fig. 1 and Fig. 2, our method achieves an ac-

curacy that is almost as good, and is much faster and

without requiring an initial estimate. This is signiﬁcant

because iterative methods are prone to failure if poorly

initialized. For instance, Lu et al.’s approach relies on

an initial estimation of the camera pose based on a

weak-perspective assumption, which can lead to insta-

bilities when the assumption is not satisﬁed. This hap-

pens when the points of the object are projected onto a

small region on the side of the image and our solution

performs more robustly under these circumstances. Fur-

thermore, if maximal precision is required our output

canbeusedtoinitializeLuet al.’s, yielding both higher

stability and faster convergence. Similarly, we can run

a Gauss-Newton scheme that improves our closed-form

solution to the point where it is as accurate as the one

produced by Lu et al.’s method when it is initialized by

our method. Remarkably, this can be done with only

very little extra computation, which means that even

with this extra step, our method remains much faster.

In fact, the optimization is performed in constant time,

and hence, the overall solution still remains O(n).

Our central idea is to write the coordinates of the

n 3D points as a weighted sum of four virtual control

points. This reduces the problem to estimating the coor-

剩余12页未读，继续阅读

评论收藏

内容反馈

#完美解决问题
#运行顺畅
#内容详尽
#全网独家
#注释完整

白菜888

粉丝: 7
资源: 74

EPnP- An Accurate O(n) Solution to the PnP Problem.pdf

EPnP阅读笔记 .pdf

恢复摄像机外参数的经典文章epnp

摄像机外参数标定（位姿估计 pose estimation）的经典文章和代码 EPNP

EPnP_matlab.zip_EPnP_epnp matlab_matlab 摄像头_多摄像头_多摄像机

IEPnP：一种基于EPnP的相机位姿迭代估计算法

EPnP_matlab.rar_MATLAB实现pnp_matlab "epnp"_matlab 求解pnp_姿态_计算机视觉

PnP位姿估计matlab工具包

EPnP_matlab.rar_EPnP_MATLAB实现pnp_PnP求解_pnp算法matlab_用Matlab做pnp

Apress.JDBC.Recipes.A.Problem.Solution.Approach.Sep.2005.pdf

Java 9 Recipes A Problem-Solution Approach(3rd) 无水印pdf

wxPython Recipes A Problem – Solution Approach 无水印原版pdf

Android Recipes A Problem-Solution Approach(5th) 无水印pdf 0分

基于正交迭代的参考点不确定相机位姿估计

PNP算法+后方交会算法

pnp恢复摄像机外参数及其源代码

epnp:epnp 的柳絮化

Matlab: rpnp

XLoader下载器

EPnP_Eigen:用Eigen实现EPnP算法

PnP solvers C++版本，包括P3Pf，Epnp等

Spring 5 Recipes A Problem-Solution Approach(4th).pdf

Ruby Recipes A Problem-Solution Approach 无水印原版pdf

Python Recipes Handbook A Problem-Solution Approach pdf 0分

EPNP根据像素坐标求解实际三维世界坐标python实现

dltmatlab代码-cvtoolbox:一些用于图像处理的实用程序代码

单目视觉的位姿估算算法

最新资源