没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

下载
第2章 布尔代数和逻辑门
数字运算是由二进制数制系统完成的,而在二进制系统中变量 X的值只能为0或1。本章将
采用1 9 世纪英国数学家乔治·布尔发展起来的开关代数来研究二进制数的行为。此数学分支
包含在布尔代数的理论中,它是现代逻辑设计的基础。
2.1 数据表示及处理
二进制数制系统中,信息(或数据)完全由二进制数字(b i t)0和1来表示。数字系统根本目
的是处理信息。这些简单的论述使我们注意到,在我们开始研究数字系统之前,有两个基本
的问题需要解决。我们怎样仅用 0和1来表示数据以及我们如何对数据进行运算 (或处理)以实现
有用的系统。
首先考虑数据表示问题。二进制系统中,数据完全是只由二进制数字 ( b i t ) 0和1来表示的。
对于二进制变量x,根据定义,x 假设值只可能是0或1。所以一位二进制变量 x 在描述只有两
种可能发生的情况时是很有用的。例如,在传统的逻辑中,象 x 这样的数经常用于表示状态的
真或假。
实际的情况要复杂得多。为了表示多于两种可能值的数据,我们可由一组按一定顺序排
列的二进制位构造出一个二进制字,并为其每一种可能的组合定义一个含义。例如,如果 a
3
、
a
2
、a
1
、a
0
为独立的二进制位,我们就可以构造一个 4 - b i t的二进制字d a t a,写作
d a t a = a
3
a
2
a
1
a
0
( 2 - 1 )
由于每位的值可以是 0或1,故d a t a 有2
4
= 1 6 种可能的组合。在本文中,用于构成二进制字
d a t a的独立的位a
i
可看成与某一特定的数据类型相联系。
在b i t 层次,数据处理的问题会有很大的不同。在此情况下,二进制变量是作为单元的输
入,而单元进行特定的数学运算,并产生一个输出 0或1。图2 . 1 表示了该数据处理问题。图中
输入变量是A, B和C,而每位变量可能的值为0或1。输出为函数 f(A, B, C),输出本身不是一个
独立的二进制变量,允许值只能为 0或1。
二进制函数的概念很容易理解。 f的值由三个输入A, B, C的值来决定。对于给定的输入, f
提供一个规则以产生输出 f = 0 或 f = 1。由于二进制函数的属性是输入和输出的值只能为 0和1,
所以二进制变量的代数与“通常的”数字范围从 0到9的代数有很大的区别。
二进制函数的定义有多种方法。真值表为完成这项任务提供了一个简单的方法。真值表
只是简单地列出所有可能的输入二进制位的组合以及每种可能输入组合对应的输出。对于 n位
输入变量,共有 2
n
可能的组合,故真值表将有 2
n
项。三个变量 A, B, C的真值表如图 2 - 2 所示。
由于2
3
= 8 ,所以共有8项输入。输出函数 f 的值位于真值表的右列。目前不要考虑函数的准确
含义,现在我们仅仅讨论真值表的形式。
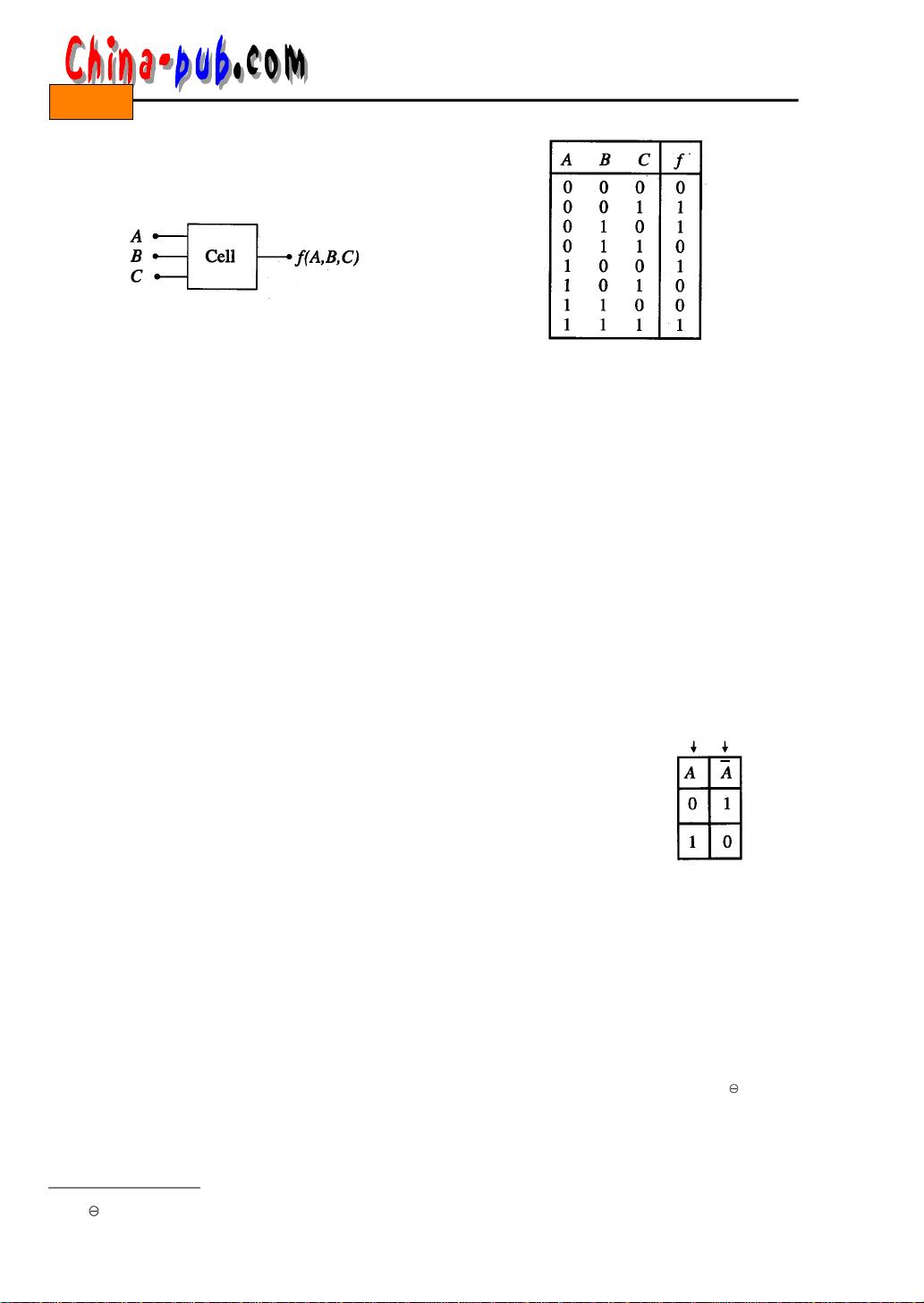
图2-1 二进制函数的通用概念 图2-2 真值表
2.2 基本逻辑运算
布尔代数的基础是一整套定义了基本函数的逻辑运算。这些函数是由通过一个或多个输
入变量并产生一位输出来实现的。本节讲述的运算是所有数字逻辑的基础。如果你肯花时间
将这些基础完全掌握,那么将非常自然地掌握数字逻辑所有领域。即使是最高级的设计者也
离不开这些基础。
2.2.1 非运算
考虑二进制变量A,N O T 运算将A转换成输出为N O T ( A),它的作用如下:
如果A= 0,那么N O T ( A ) = 1 ;
如果A= 1,那么N O T ( A ) = 0。
N O T运算的功能就是将变量的值从 0变到1或从1变到0
N O T 运算的真值表如图 2 - 3 所示。对于输入 A,我们通常将
N O T ( A ) 简单地标识为
−
A或A ' 。注意,对于一位输入变量,共有 2
1
= 2
种可能的输入组合 (A= 0 或A= 1 ) 。根据此论述,我们也可将
−
A称为A的
补码。
二进制运算的另一种表示方法是用代数形式的符号方式来书写。
例如,我们把N O T 函数写成 f (A),其中A为输入,那么
f (A) =
−
A ( 2 - 2 )
就将 f 定义为N O T 运算。通过验证,此式提供的信息与真值表相同。
代数函数和表格列示在处理数字系统的理论方面是很有用的。但是,当我们想用门单元
来设计逻辑网络时,采用称为逻辑图的图形描述更为方便。逻辑图中我们用各种类型的图形
符号来表示逻辑功能。使用这种方式描述数字系统可同时表示出用于构成系统的逻辑模块以
及各单元间的互连关系。
N O T 函数的图形符号如图 2 - 4 a )所示;N O T函数也称为反相器,其运算称为取反 。根据
该符号的定义,输入变量为 A时输出为
−
A。在电子学中三角形十分常见,它表示的是称为缓冲
器的逻辑门;作为选择,你也可使用将在第 2 . 9 节中描述的更为通用的符号。通常在逻辑上缓
第2章 布尔代数和逻辑门 23
下载
输入
输出
图2-3 NOT的真值表
输入 输出
术语反相器的采用是因为当输入为0时它的输出为1,反过来也成立。

冲器的输出与输入是相同的,如图 2 - 4 b ) 所示:如果输入为 A,那么其输出也为A。虽然缓冲器
不改变逻辑状态,但它可用于表示某些类型电子网络中需要的附加的电“驱动能力”。 无论
何时,只要用逻辑图表示 N O T 运算,我们都将采用图中所示的“气泡”标识。气泡可以出现
在逻辑门的输入或输出,这种简化的标识将会经常使用到。
图2-4 反相器和缓冲器符号
Not符号
2.2.2 或门
现在我们来考虑带有两个独立输入位的情形。我们将这两个输入称为 A和B。由于两位中
的每一位的值均可假设为 0或1,所以共产生 2
2
= 4 种可能的输入组合。这些组合为 A B =00, 01,
10, 11。
我们讲述的第一个 2 - 输入逻辑门实现的运算为 O R 运算,由于它有两个输入,所以在我们
的讨论中,这种特别情况被称之为 O R 2门。当输入为A和B时,O R运算描述如下:
如果 A=1 或 B=1, 或 A=1 且 B= 1,
那么
A OR B= 1
否则
A OR B= 0
逻辑O R运算需要2个或更多的输入
这可重新表述为如果输入值有一个为 1,那么A OR B= 1。因为函数的值只能是0或1,所以
它暗示着如果A= 0且B= 0,那么A OR B= 0。我们通常采用符号“+”来标识 O R运算:
A OR B =A+B (2-3)
若可以排除将二进制运算与标准加法运算相混淆的可能性,上式标识方法将十分常用。
O R 函数的真值表如图 2 - 5 所示。注意到四个输入组合中的每一个都是以不同的列式行来描述
的。用于描述O R 运算的另一个符号为:
A OR B =A∨B ( 2 - 4 )
但在讨论中我们将不使用此符号。
描述O R函数常用的图形符号如图2 - 6所示,图中输入A和B在符号的左边,输出A OR B在右
边,其输出值如真值表所示。注意到O R“逻辑门”的特别的形式可使我们快速地识别其运算。
图2-5 OR的真值表 图2-6 OR2逻辑门符号2个输入的O R门
24 数字系统设计基础教程
下载
a) 反相器符号 b) 缓冲器符号
剩余18页未读,继续阅读
资源评论

lemon_2014
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功