离散数学,布尔代数,数理逻辑
根据给定文件的信息,我们可以提炼出以下几个重要的知识点: ### 一、离散数学与计算机科学 **1.1 计算机科学与离散数学的关系** - **定义**: 计算机科学是一门涉及计算机软件和硬件的综合性学科,其特点之一就是“离散性”。 - **离散数学**: 是一门研究离散量结构及其相互关系的学科,它为计算机科学提供了必要的数学基础。 **1.2 离散数学的重要性** - **必备课程**: 对于计算机专业的学生来说,离散数学是必修的核心课程之一。 - **应用广泛**: 离散数学不仅应用于理论层面的研究,也在实际编程和算法设计中有广泛的应用。 ### 二、布尔代数 **2.1 布尔代数简介** - **定义**: 布尔代数是以布尔运算为基础的一种代数系统,通常用于逻辑电路设计和计算机程序设计。 - **基本运算**: 包括逻辑加(或)、逻辑乘(与)、逻辑非(非)等。 - **布尔表达式**: 可以用来表示和解决逻辑问题,如电路设计中的开关状态分析。 **2.2 布尔代数的应用** - **电子科学**: 在电子科学中,布尔代数可以用于电路的设计和分析。 - **数理逻辑**: 在数理逻辑中,布尔代数被用来研究命题逻辑和谓词逻辑。 ### 三、集合论初步 **3.1 集合的基本概念** - **定义**: 集合是由一些确定对象组成的整体。 - **表示方法**: 包括列举法、描述法和谓词表示法。 - **常见集合**: 如空集、单元素集合、全集等。 **3.2 集合的关系** - **相等**: 如果两个集合具有相同的元素,则这两个集合相等。 - **子集**: 若一个集合中的所有元素都属于另一个集合,则前者是后者的子集。 - **真子集**: 若集合A是集合B的子集但不等于B,则A是B的真子集。 **3.3 集合的运算** - **交集**: A∩B 表示同时属于集合A和B的元素。 - **并集**: A∪B 表示属于集合A或B的元素。 - **差集**: A-B 表示属于集合A但不属于集合B的元素。 - **补集**: A' 表示全集中不属于集合A的元素。 - **对称差**: A⊕B 表示属于A或B但不属于两者都有的元素。 **3.4 运算律** - **交换律**: A∩B = B∩A, A∪B = B∪A。 - **结合律**: (A∩B)∩C = A∩(B∩C), (A∪B)∪C = A∪(B∪C)。 - **分配律**: A∩(B∪C) = (A∩B)∪(A∩C), A∪(B∩C) = (A∪B)∩(A∪C)。 - **等幂律**: A∩A = A, A∪A = A。 - **零一律**: A∩E = A, A∪∅ = A, A∩∅ = ∅, A∪E = E。 - **互补律**: A∩A' = ∅, A∪A' = E, (A')' = A。 - **德摩根律**: (A∩B)' = A'∪B', (A∪B)' = A'∩B'。 - **吸收律**: A∪(A∩B) = A, A∩(A∪B) = A。 ### 四、幂集、n元有序组与笛卡尔积 **4.1 幂集** - **定义**: 幂集是指由一个集合的所有子集组成的集合。 - **基数**: 一个集合的基数是指该集合中元素的数量。 - **幂集的基数**: 设集合A的基数为n,则其幂集的基数为2^n。 **4.2 n元有序组** - **定义**: n元有序组是指按照特定顺序排列的n个对象组成的序列。 - **表示**: (a1, a2, …, an)。 - **相等**: 两个n元有序组相等当且仅当它们对应的每个元素相等。 **4.3 笛卡尔积** - **定义**: 两个集合A和B的笛卡尔积是指所有形如(a, b)的有序对组成的集合,其中a属于A,b属于B。 - **表示**: A×B。 - **扩展**: 多个集合之间的笛卡尔积也可以类似定义。 以上内容覆盖了离散数学中的核心概念,包括布尔代数、集合论的基础知识以及相关的运算和定律,这些都是计算机科学中不可或缺的基础知识。


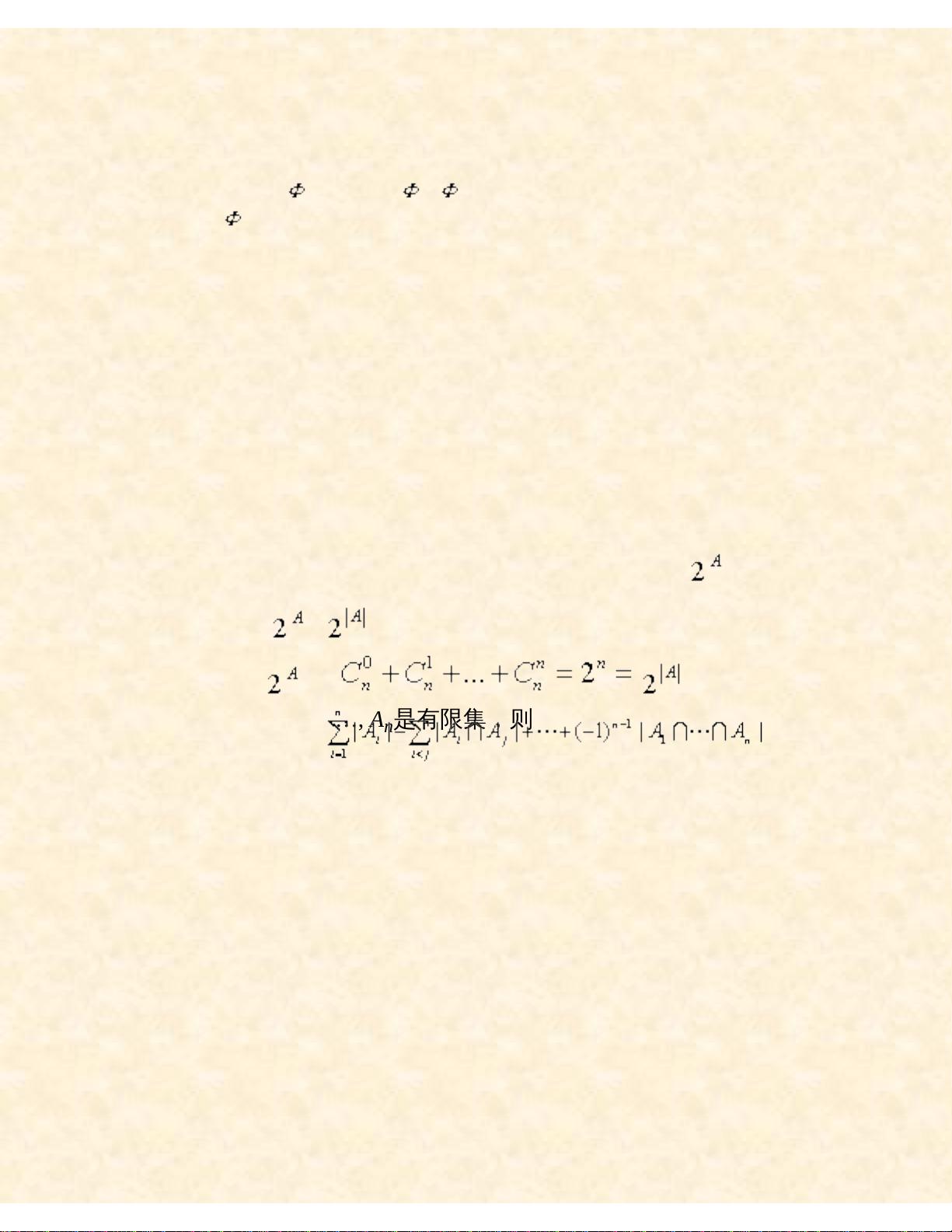

剩余64页未读,继续阅读

- 粉丝: 5
- 资源: 17
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功