GWO-GPR灰狼算法优化高斯过程回归多变量回归预测

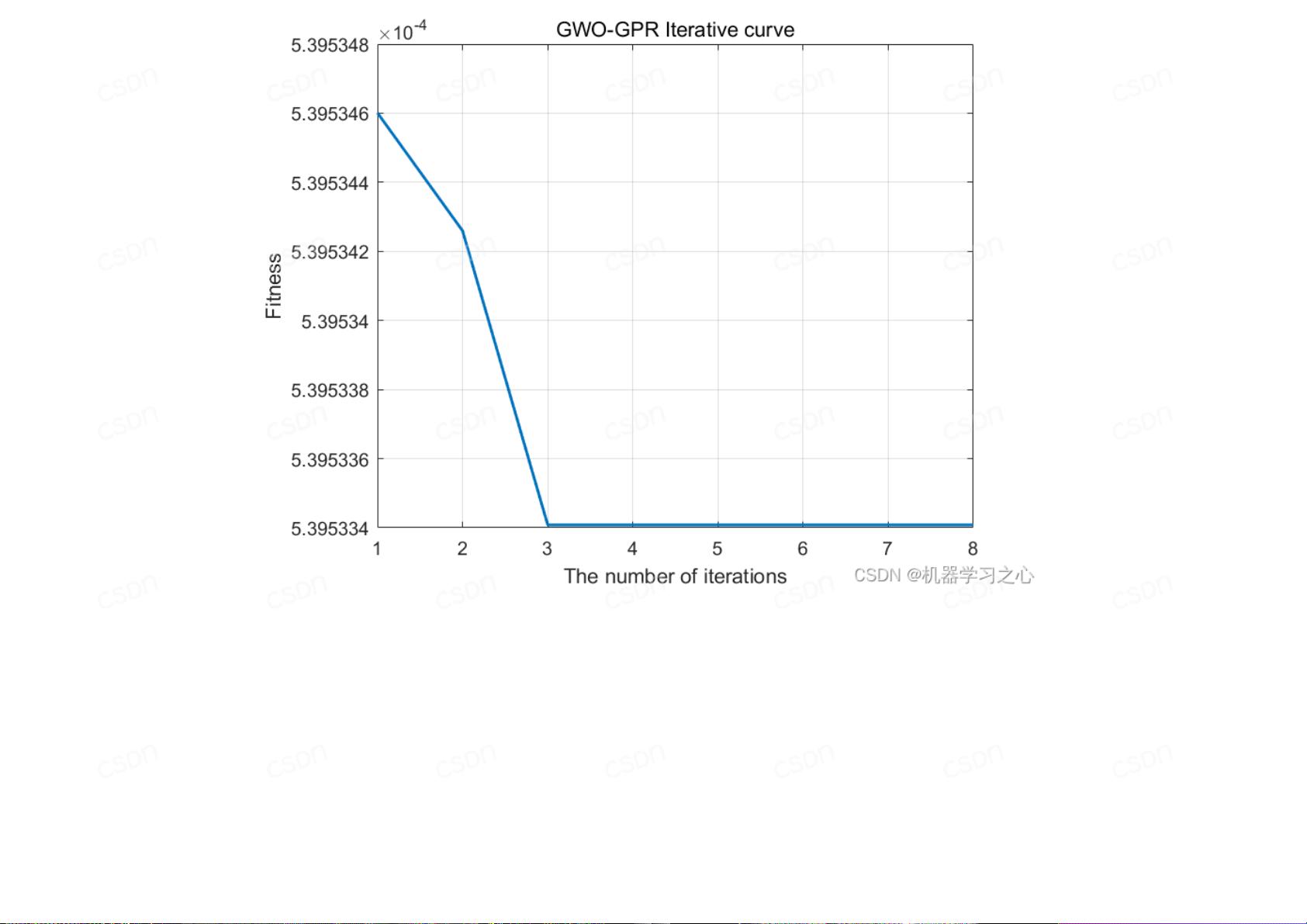
Matlab实现GWO-GPR灰狼算法优化高斯过程回归多变量回归预测 1.Matlab实现GWO-GPR灰狼算法优化高斯过程回归多变量回归预测（完整源码和数据) 2.输入多个特征，输出单个变量，多输入单输出回归预测； 3.多指标评价，评价指标包括：R2、MAE、MSE、RMSE等，代码质量极高； 4.粒子群算法优化参数为：优化核函数超参数 sigma，标准差，初始噪声标准差； 5.excel数据，方便替换，运行环境2018及以上,可在下载区获取数据和程序内容。 根据给定的信息，本文将详细解析"GWO-GPR灰狼算法优化高斯过程回归多变量回归预测"这一主题，涵盖其基本概念、实现方法、评价指标以及应用场景。 ### 基本概念 #### 1. **灰狼优化算法(GWO)** 灰狼优化算法是一种启发式优化算法，模仿了灰狼的社会等级结构和狩猎行为。它通过模拟狼群中的领袖（Alpha）、副领袖（Beta）和追随者（Delta）的角色来寻找问题的最优解。在每次迭代过程中，这些角色会根据适应度值更新它们的位置，逐渐逼近全局最优解。 #### 2. **高斯过程回归(GPR)** 高斯过程回归是一种非参数化贝叶斯方法，用于回归分析。它通过定义一个由均值函数和协方差函数（也称为核函数）组成的高斯过程来建模输出变量与输入变量之间的关系。GPR能够提供预测分布的概率信息，而不仅仅是预测值本身，这使得它非常适合处理具有不确定性的回归任务。 ### 实现方法 #### 1. **GWO-GPR结合** 在这个实现中，GWO被用作优化器来调整GPR中的核函数超参数。具体来说，GWO的目标是找到最佳的核函数超参数集，以最小化预测误差。这里提到的超参数包括： - **sigma**：控制核函数平滑程度的参数。 - **标准差**：用于衡量观测噪声的大小。 - **初始噪声标准差**：设置初始观测噪声的标准差。 通过GWO优化这些超参数，可以显著提高GPR模型的预测性能。 #### 2. **多输入单输出回归预测** 在本项目中，GWO-GPR被应用于多输入单输出的回归预测任务。这意味着模型接受多个特征作为输入，并预测一个单一的输出变量。这种类型的预测任务广泛存在于各种实际应用中，例如经济预测、环境监测等领域。 ### 评价指标 为了评估GWO-GPR模型的性能，使用了多种评价指标，包括但不限于： - **R² (决定系数)**：衡量模型解释变量之间变异性的比例。值越接近1，表示模型拟合越好。 - **MAE (平均绝对误差)**：计算预测值与真实值之间的平均绝对差异，用于评估预测的准确性。 - **MSE (均方误差)**：测量预测值与实际值之间的平均平方差，强调较大误差的影响。 - **RMSE (均方根误差)**：MSE的平方根，与MAE类似，但对较大的误差更敏感。 这些指标提供了全面的视角来评估模型的性能，并帮助研究人员根据实际需求选择最适合的模型配置。 ### 应用场景 GWO-GPR特别适用于那些数据集包含大量特征并且需要精确预测的应用场景。例如，在金融领域，可以通过多变量回归预测股票价格或汇率变动；在环境保护领域，可以预测空气或水质的变化趋势；在工业生产中，则可用于预测设备故障概率等。 ### 总结 "GWO-GPR灰狼算法优化高斯过程回归多变量回归预测"是一项强大的技术，它结合了灰狼优化算法的强大搜索能力和高斯过程回归的灵活性，为多输入单输出的回归预测任务提供了高效的解决方案。通过对模型进行仔细的优化并使用合适的评价指标，可以在各种实际应用中实现准确可靠的预测结果。对于希望深入探索此领域的研究者而言，掌握这些技术和方法是非常有价值的。