Mann-Whitney Test Independent Samples _ Real Statistics Using Ex...

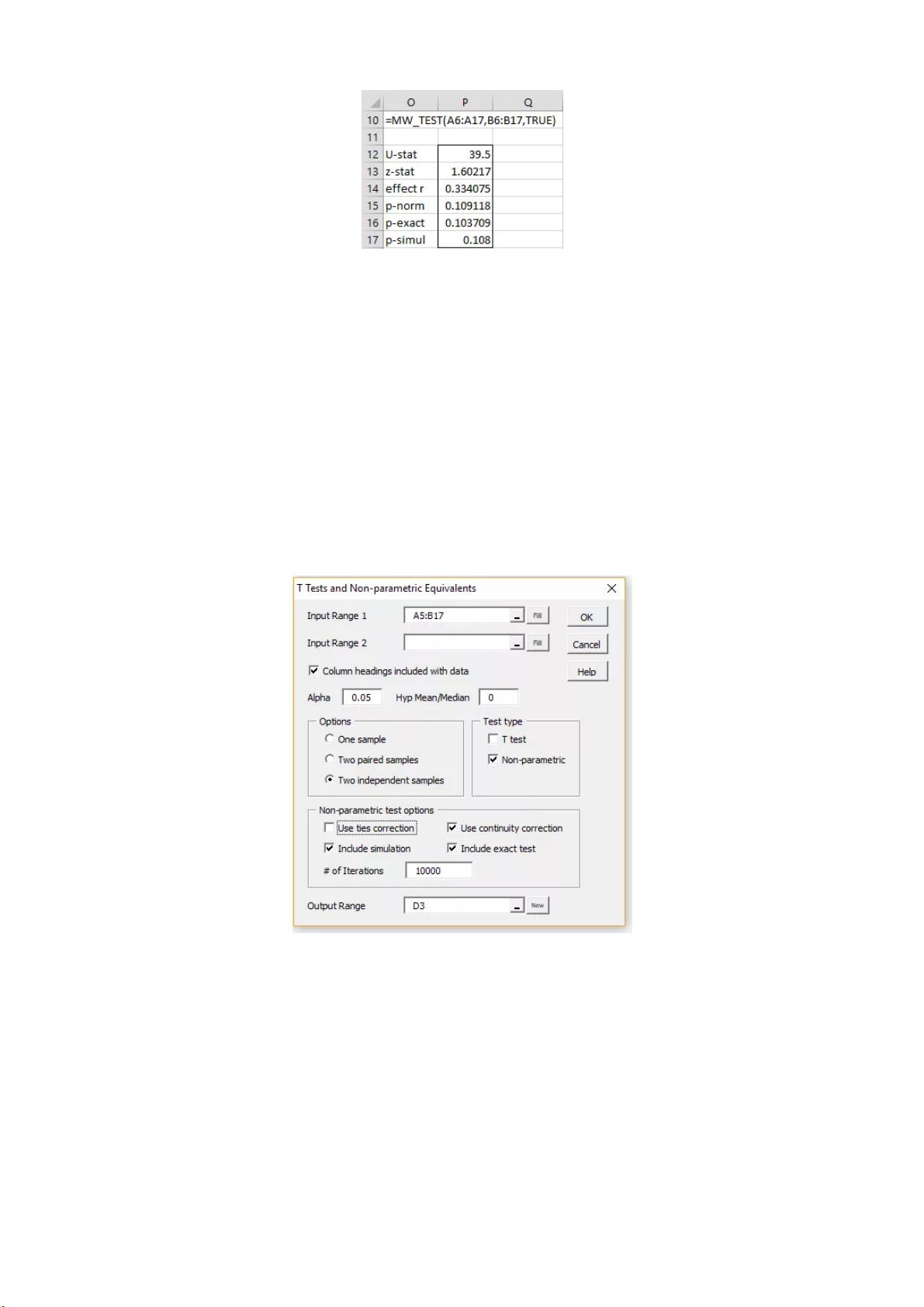
曼-惠特尼U检验（Mann-Whitney Test）是一种非参数检验方法，用于比较两个独立样本的中位数是否存在显著差异。它实际上是威尔科克森秩和检验（Wilcoxon Rank-Sum Test）的一个替代形式，两者在逻辑上是等价的。曼-惠特尼U检验不依赖于数据的分布形态，对异常值不敏感，适用于样本量较小且数据不符合正态分布的情况。 在进行曼-惠特尼U检验时，需要对两个独立样本的观测值进行排名，并对排名后的数据进行特定的统计计算以得到检验统计量U。在某些情况下，还需要对检验统计量U进行标准化处理，以便于分析其显著性水平。具体计算方法如下： 1. 对两个独立样本中的观测值进行排序，将两组数据混合后赋予相应的秩次（排名）。 2. 对每个样本的秩次求和，得到两个样本的秩和R1和R2。 3. 根据样本容量n1和n2，以及秩和R1和R2，计算曼-惠特尼U统计量。U统计量的计算公式为U1=n1*n2+ n1*(n1+1)/2 - R1和U2=n1*n2+ n2*(n2+1)/2 - R2，取较小的U值作为最终的U统计量。 4. 通过查表得到在特定显著性水平α下的临界值，如果计算出的U值小于临界值，则拒绝原假设（两个样本的中位数相同），反之则不拒绝。 在Excel中使用曼-惠特尼U检验的步骤如下： a. 选择包含两个独立样本数据的两个区域。 b. 通过Real Statistics Using Excel软件包提供的曼-惠特尼U检验工具来计算U值及对应的P值。 c. 根据计算结果判断是否拒绝原假设。 曼-惠特尼U检验还有以下几个重要性质： 性质1：对于足够大的样本量n1和n2，U统计量近似服从均值为μ，方差为σ2的正态分布。 性质2：当存在大量的数据点时，U统计量可以用正态分布进行近似。对于大样本，可以使用z分数来进行统计推断，通过正态分布来估计p值。 性质3：当数据中存在大量的并列排名（ties）时，需要对U统计量的方差进行修正以获得更准确的结果。 在处理并列排名时，曼-惠特尼U检验会使用修正的方差公式。对于并列排名的处理，会引入一个额外的调整参数，来确保检验的准确性。 在Excel中实施曼-惠特尼U检验时，还需要注意连续性校正的问题。由于我们是通过连续分布来逼近离散分布的，因此在计算z分数时通常会应用一个连续性校正因子（例如减去0.5）。这样做的目的是为了减小由离散分布逼近所带来的误差。 曼-惠特尼U检验是一种适用于小样本数据的非参数检验方法，能够有效地比较两个独立样本的中位数差异。该方法在Excel中可以通过Real Statistics Using Excel插件来实现，操作简便，且能够提供准确的统计推断。在实际操作中，用户需要注意样本的适用性、并列排名的处理、以及连续性校正的应用等多个细节，以确保检验结果的可靠性和准确性。