### CT锥形束FDK重建算法详解
#### 一、概述
CT(Computed Tomography,计算机断层扫描)技术在医疗诊断、工业检测等领域发挥着重要作用。随着技术的发展,CT成像技术也在不断进步,其中锥形束CT因其在空间分辨率、数据采集速度以及射线利用率方面的优势而备受关注。本篇文章将详细介绍CT锥形束FDK重建算法及其相关知识点。
#### 二、基础知识
##### 1. 中心切片定理
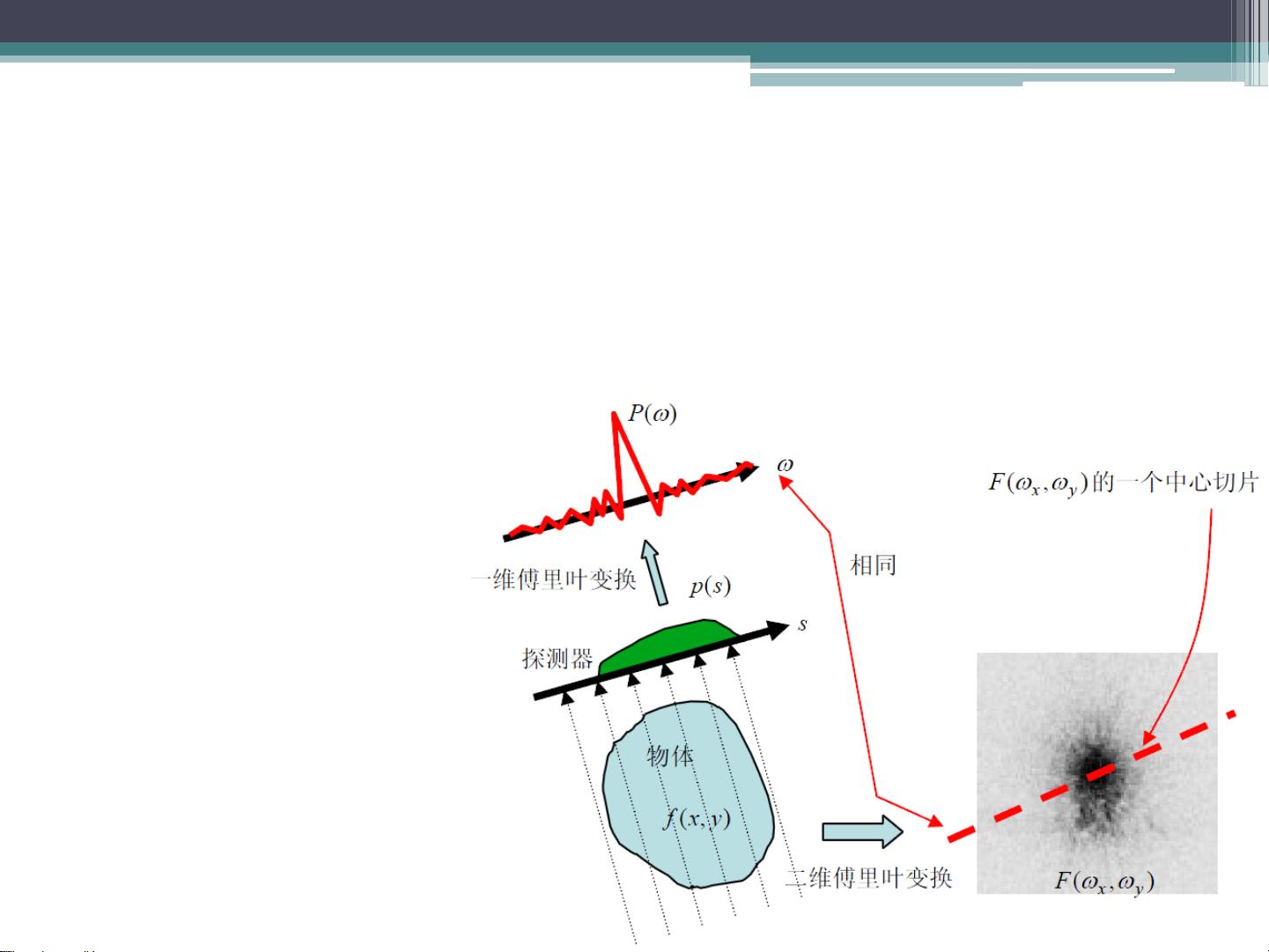
中心切片定理是图像重建的基础理论之一,它指出:二维函数投影的一维傅里叶变换等于函数的二维傅里叶变换沿与探测器平行的方向过原点的片段。这一原理同样适用于三维情况,即三维函数投影的二维傅里叶变换等于函数的三维傅里叶变换沿与探测器平行的方向过原点的片段。这一理论为后续的图像重建提供了数学基础。
##### 2. FBP算法
FBP(Filtered Back Projection,滤波反投影)算法是一种广泛应用于CT图像重建的经典方法。它包括两个主要步骤:首先对投影数据进行滤波,然后进行反投影。FBP算法可以进一步细分为平行束FBP算法、扇形束FBP算法等,根据不同的数据采集方式选择相应的算法。
#### 三、CT图像重建算法
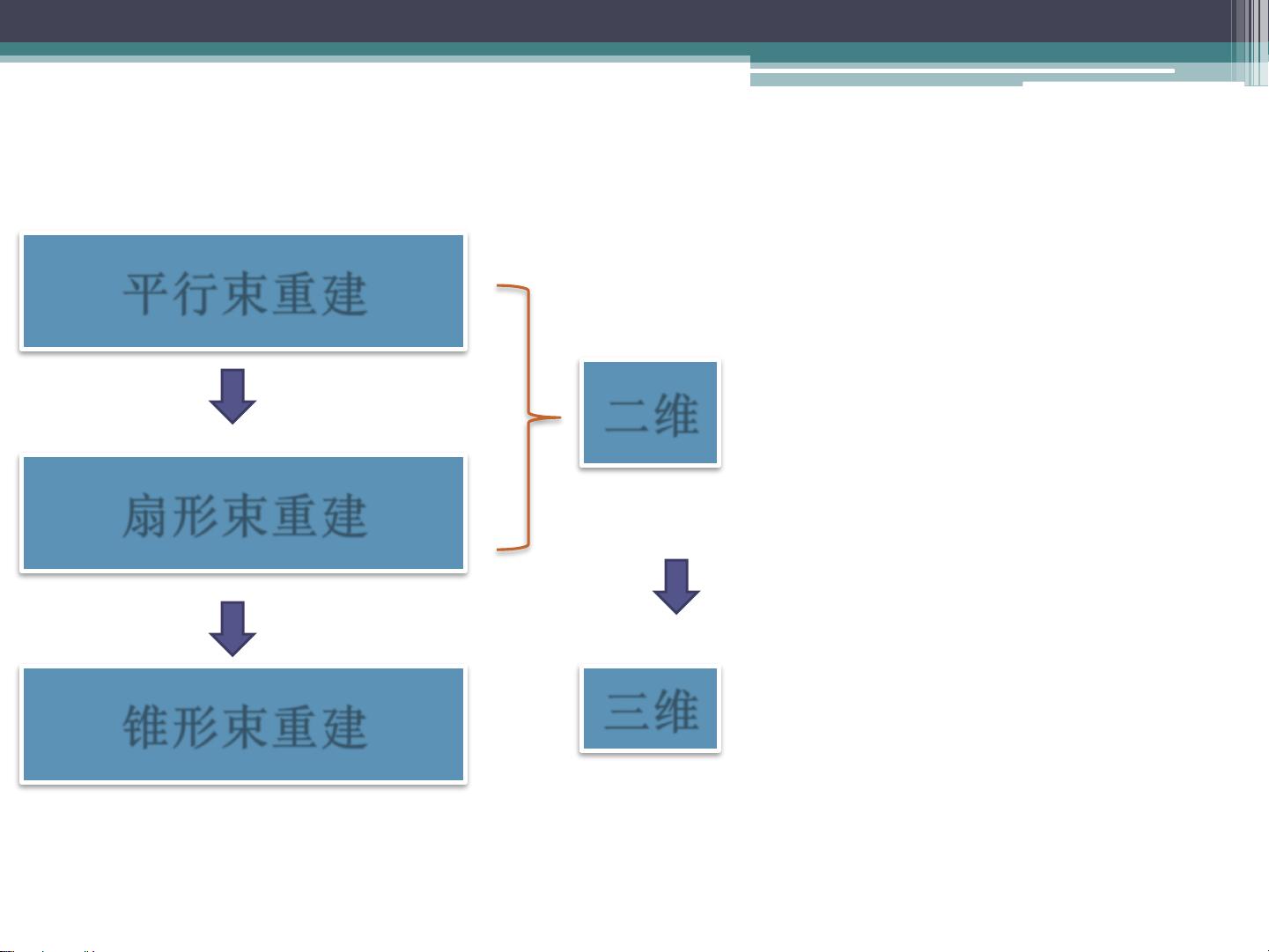
##### 1. 平行束重建
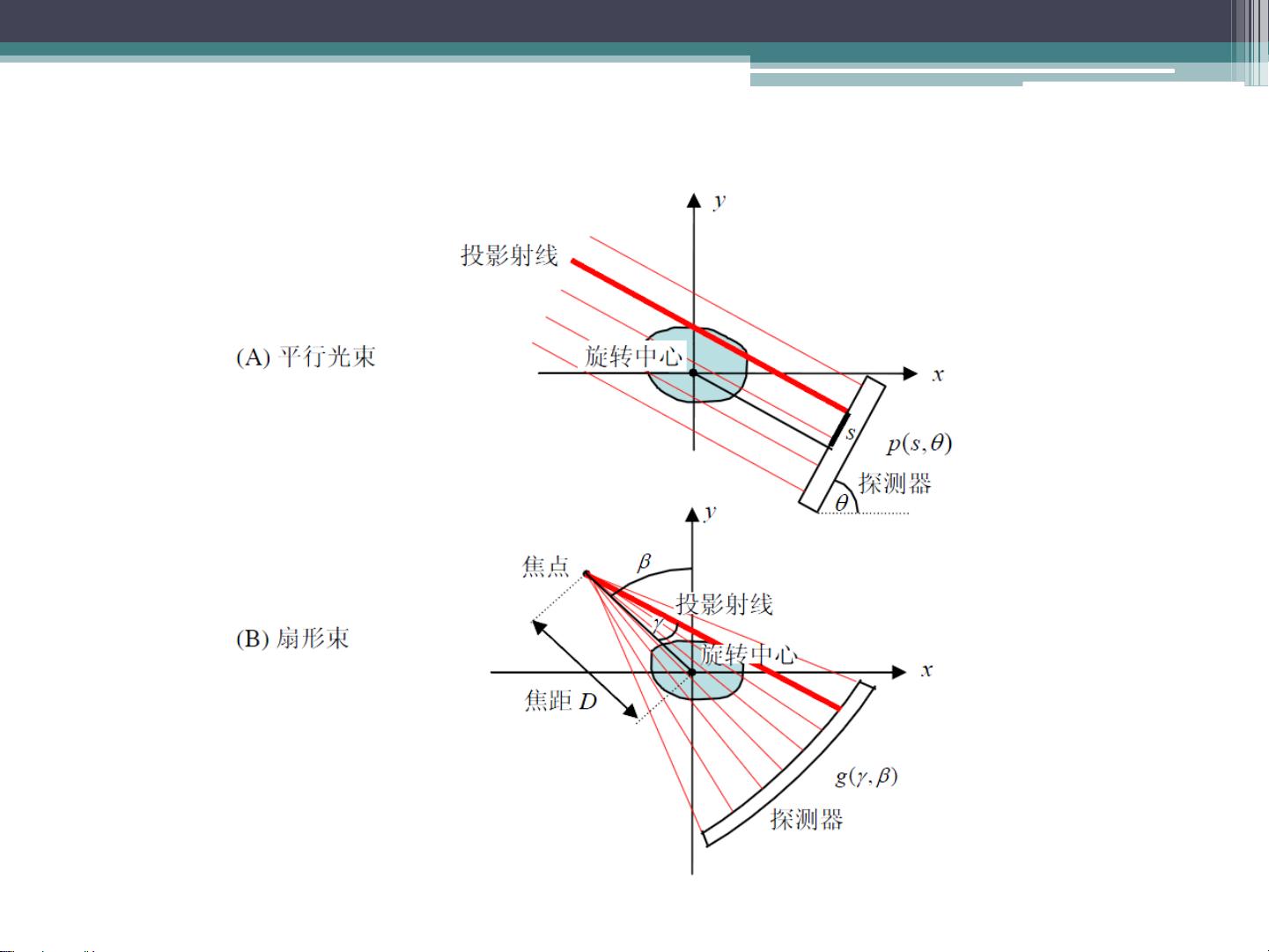
平行束重建是最基本的一种CT图像重建方式。它基于平行束FBP算法,该算法主要包括三个步骤:对投影数据进行加权预处理、对预处理过的数据逐行进行一维斜坡滤波、把滤波后的数据做加权反投影。这里的权函数取决于重建点到焦点的距离。
##### 2. 扇形束重建
扇形束重建是在平行束重建的基础上发展起来的,能够更高效地利用数据。扇形束FBP重建算法也包括三个步骤:对投影数据做加权预处理、对预处理过的数据逐行进行一维斜坡滤波、把滤波后的数据做加权反投影。与平行束重建不同的是,扇形束重建中的权函数取决于重建点到焦点的距离。
##### 3. 锥形束重建
###### (1)三维锥形束FDK算法
FDK(Feldkamp-Davis-Kress)算法是由Feldkamp、Davis和Kress共同提出的一种针对锥形束图像重建的方法。该算法主要用于处理圆形焦点轨迹的情况,其基本思想是将锥形束图像重建问题转换为扇形束图像重建问题。具体步骤如下:
- 对投影数据做加权预处理(乘以一个余弦函数cosα);
- 对预处理过的数据逐行进行一维斜坡滤波;
- 把滤波后的数据做加权反投影。
FDK算法虽然简单易实现,但当锥形束的锥形张角较大时,重建的物体形状会出现扭曲并产生伪影。
###### (2)FDK算法特点
- **优点**:算法简单,易于实现;
- **缺点**:锥形束张角较大时,重建结果会出现较大的偏差,导致图像质量下降。
###### (3)FDK衍生算法
- **Grangeat算法**:该算法的基本思路是将锥形束图像重建问题转换为三维拉东变换问题。其特点是需要将锥形束数据重新排列成拉东数据,这可能会引入一定的误差。但如果所用的轨道满足Tuy条件,则可以得到精确的重建图像。
- **Katsevich算法**:这是一种真正的FBP算法,特别适合螺旋轨道的数据。该算法的滤波过程是移动不变的,反投影也是锥形束的反投影。但由于算法的限制条件,没有充分利用所测到的投影数据,并且选择滤波方向需要一定的技巧。
#### 四、FDK算法的CUDA加速
随着计算硬件的发展,尤其是GPU(Graphics Processing Unit,图形处理器)的高性能并行计算能力被广泛应用,FDK算法的CUDA(Compute Unified Device Architecture,统一计算设备架构)加速成为可能。通过CUDA,可以显著提高图像重建的速度。具体实现包括三个主要步骤:
1. **加权阶段**:对投影数据进行逐点加权。
2. **滤波阶段**:通过补零操作,利用CUDA提供的库进行逐行傅立叶变换,并与滤波函数进行逐点相乘,最后执行傅立叶逆变换。
3. **反投影阶段**:对重建物体进行逐点反投影。
### 结论
CT锥形束FDK重建算法及其相关衍生算法在现代CT成像技术中占据着重要地位。通过深入理解这些算法的工作原理和技术细节,可以更好地利用现代计算资源提高图像重建的质量和效率。未来,随着计算技术的不断进步,这些算法还将继续得到改进和发展。