摄像头坐标系，图像坐标系，世界坐标系的转换

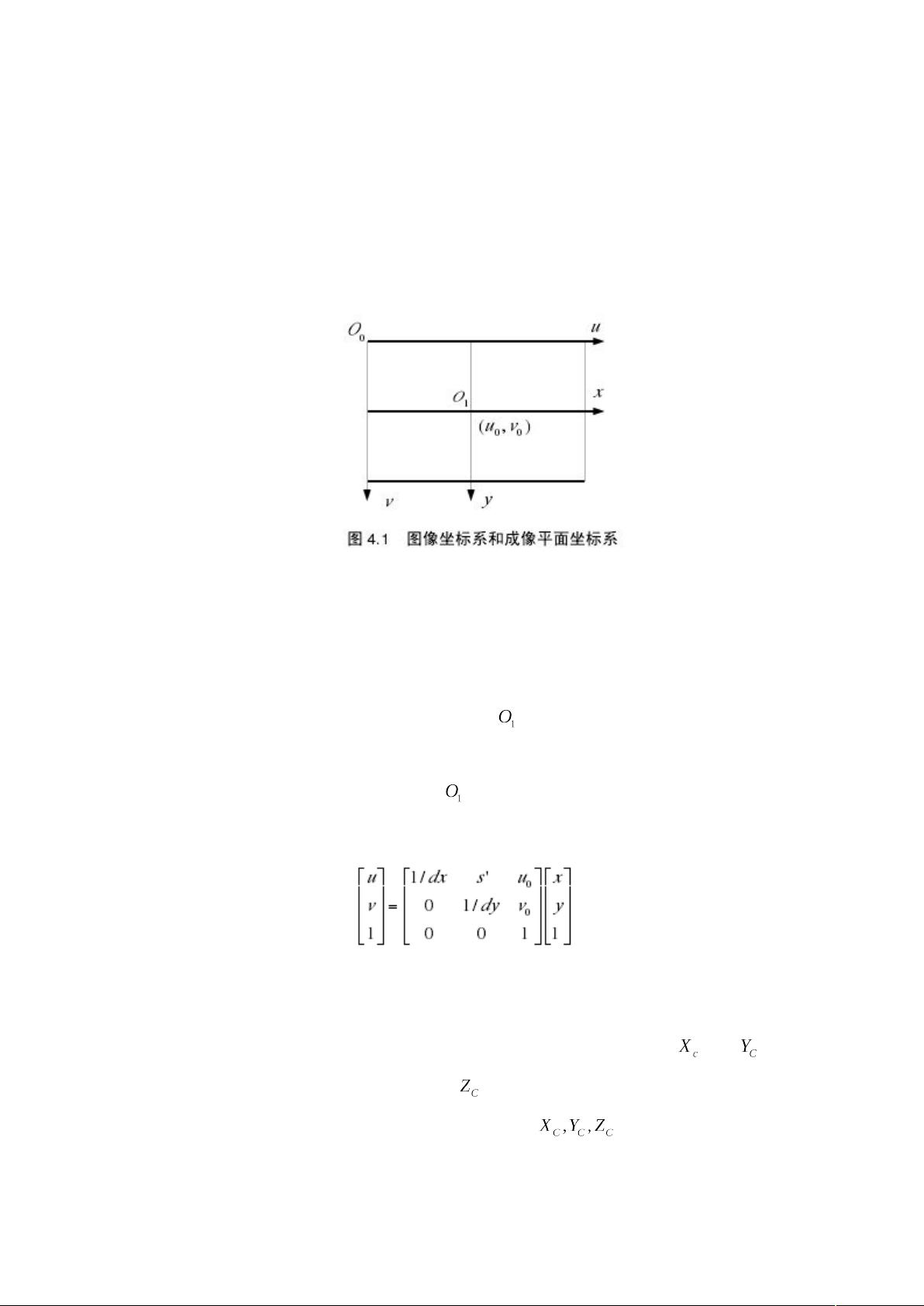
### 摄像头坐标系、图像坐标系与世界坐标系的转换 #### 一、图像坐标系（Pixel Coordinate System） 图像坐标系是基于数字图像的像素排列建立的坐标系统。在计算机内存中，数字图像通常被存储为二维数组的形式，数组中的每个元素代表一个像素（pixel），该像素的值反映了图像点的亮度或灰度等级。如图4.1所示，图像上定义了一个直角坐标系\( u-v \)，其中每个像素的坐标\((u, v)\)分别对应于像素在数组中的列数和行数。因此，\((u, v)\)是以像素为单位的图像坐标系坐标。 #### 二、成像平面坐标系（Retinal Coordinate System） 虽然图像坐标系能够提供像素在图像中的位置信息，但这些坐标仅表示像素位于数字图像中的哪一行哪一列，并没有用物理单位表示像素在图像中的实际位置。因此，需要建立一个以物理单位（例如毫米）表示的成像平面坐标系\( x-y \)，如图4.1所示。在这个坐标系中，原点\( O' \)定义在摄像机光轴与图像平面的交点处，称为图像的主点（principal point）。通常情况下，主点位于图像中心，但有时会因为摄像机制造工艺的原因而略有偏移。\((u_0, v_0)\)表示主点在图像坐标系下的坐标，每个像素在\( x \)轴和\( y \)轴方向上的物理尺寸分别为\( dx \)、\( dy \)。两个坐标系之间存在以下关系： \[ \begin{cases} x = (u - u_0) \cdot dx \\ y = (v - v_0) \cdot dy \end{cases} \] 其中，\( s' \)表示因摄像机成像平面坐标轴相互不正交而产生的倾斜因子（skew factor）。 #### 三、摄像机坐标系（Camera Coordinate System） 摄像机成像的几何关系可通过图4.2展示。其中，\( O \)点被称为摄像机的光心（optical center），\( X_c \)轴和\( Y_c \)轴与成像平面坐标系的\( x \)轴和\( y \)轴平行，\( Z_c \)轴为摄像机的光轴，与图像平面垂直。光轴与图像平面的交点为图像主点\( O' \)。由点\( O \)与\( Z_c \)轴组成的直角坐标系称为摄像机坐标系。\( OO' \)代表摄像机的焦距。 #### 四、世界坐标系（World Coordinate System） 为了描述摄像机和物体在环境中的位置，需要选择一个参考坐标系，即世界坐标系。摄像机坐标系和世界坐标系之间的关系可通过旋转矩阵\( R \)与平移向量\( t \)来描述。空间中的一点\( P \)在世界坐标系和摄像机坐标系下的齐次坐标分别为\( [X_w, Y_w, Z_w, 1]^T \)和\( [X_c, Y_c, Z_c, 1]^T \)，并且存在以下关系： \[ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} R & t \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \] 其中\( R \)是3×3的正交单位矩阵，\( t \)是3维平移向量，\( M_1 \)是两个坐标系之间的联系矩阵。 #### 五、摄像机线性模型与透视投影 透视投影是成像中最常用的模型，可以用针孔成像模型近似表示。其特征在于所有来自场景的光线均通过一个投影中心，它对应于透镜的中心。经过投影中心且垂直于图像平面的直线称为投影轴或光轴，如图4.3所示。其中\( XYZ \)是固定在摄像机上的直角坐标系，遵循右手定则，其原点位于投影中心，\( Z \)轴与投影重合并指向场景，\( X \)轴和\( Y \)轴与图像平面的坐标轴\( x' \)和\( y' \)平行，\( XY \)平面与图像平面的距离\( f \)为摄像机的焦距。在实际摄像机中，图像平面位于投影中心之后距离为\( f \)的位置，其投影图像是倒立的。为了避免图像倒立，假设有一个虚拟成像平面\( x'y'z' \)位于投影中心前方，点\( P \)在图像平面上的投影位置\( (x, y) \)可以通过计算点\( P \)的视线与虚拟成像平面的交点获得。 摄像机坐标系与成像平面坐标系之间的关系为： \[ \begin{cases} x = f \frac{X_c}{Z_c} + u_0 \\ y = f \frac{Y_c}{Z_c} + v_0 \end{cases} \] 其中，\((x, y)\)为点\( P \)在成像平面坐标系下的坐标，\([X_c, Y_c, Z_c]\)为空间点\( P \)在摄像机坐标系下的坐标。使用齐次坐标与矩阵形式表示： \[ \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & u_0 \\ 0 & f & v_0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_c / Z_c \\ Y_c / Z_c \\ 1 \end{bmatrix} \] 将以上关系代入，得到图像坐标系和世界坐标系之间的关系： \[ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K [R | t] \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \] 其中，\( K = \begin{bmatrix} f & s & u_0 \\ 0 & f & v_0 \\ 0 & 0 & 1 \end{bmatrix} \)，\( [R | t] \)完全由摄像机相对于世界坐标系的方位决定，称为摄像机外部参数矩阵；\( K \)只与摄像机内部结构有关，称为摄像机内参数矩阵，其中\((u_0, v_0)\)为主点坐标，\( f \)为焦距，\( s \)描述两图像坐标轴倾斜程度的参数。矩阵\( P \)为3×4矩阵，称为投影矩阵，即从世界坐标系到图像坐标系的转换矩阵。 如果已知摄像机的内外参数，则已知投影矩阵\( P \)，对于任何空间点，如果已知其三维坐标\( [X_w, Y_w, Z_w] \)，就可以求出其图像坐标点的位置\((u, v)\)。然而，如果只知道空间某点的图像点坐标\((u, v)\)，即使已知投影矩阵，也无法唯一确定其空间坐标，它只对应于空间中的一条直线。这意味着单目摄像头只能测量平面信息，无法获取深度信息。