没有合适的资源?快使用搜索试试~ 我知道了~
线性代数在数学建模中的应用举例 2.pdf
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 130 浏览量
2023-05-20
08:24:44
上传
评论 1
收藏 737KB PDF 举报
温馨提示
"线性代数在数学建模中的应用举例 2" 本文主要讨论了线性代数在数学建模中的应用,通过两个实例来展示线性代数在数学建模中的重要性。 我们讨论了基因频率的表示问题。在这个问题中,我们使用单位向量来表示每一个群体的基因频率,然后利用向量间的夹角来表示两个对应的群体间的“距离”。这里,我们使用了 cosθ = a1·a2 来计算两个向量之间的夹角,然后通过反余弦函数来计算对应的角度。通过这种方法,我们可以计算出不同群体间的基因“距离”,并发现班图人与英国人之间的基因“距离”最小,而爱斯基摩人与班图人之间的基因“距离”最大。 我们讨论了四面体的体积问题。在这个问题中,我们使用了向量的数量积来计算四面体的体积。我们建立了一个坐标系,并设定了四面体的六条棱长分别为 l, m, n, p, q, r。然后,我们使用了向量 OA, OB, OC 来计算四面体的体积 V。我们发现,V 等于以向量 OA, OB, OC 组成右手系时,以它们为棱的平行六面体的体积 V6 的一半。我们使用了向量的数量积的坐标表示,来计算四面体的体积 V。 在这两个实例中,我们可以看到线性代数在数学建模中的重要性。线性代数提供了一种-powerful工具,用于解决数学建模中的问题。通过使用向量和矩阵,我们可以更方便地解决问题,并获得更加准确的结果。 本文展示了线性代数在数学建模中的应用,通过两个实例来展示线性代数在数学建模中的重要性。我们可以看到,线性代数提供了一种-powerful工具,用于解决数学建模中的问题。
资源推荐
资源详情
资源评论
线性代数在数学建模中的应用举例 2
线性代数在数学建模中的应用举例
1 基因间“距离”的表示
在ABO 血型的人们中,对各种群体的基因的频率进行了研究。如果我们把
四种等位基因 A
1
,A
2
,B,O 区别开,有人报道了如下的相对频率,见表 1、1。
表 1、1 基因的相对频率
爱斯基摩人 f1
i
0.2914
0、0000
0.0316
0、6770
1.000
班图人
f
2i
0.1034
0、0866
0、1200
0.6900
1、000
英国人
f
3i
0、2090
0、0696
0、0612
0.6602
1、000
朝鲜人 f4i
0、2208
0.0000
0、2069
0、5723
1、000
A
1
A
2
B
O
合计
问题 一个群体与另一群体的接近程度如何?换句话说 ,就就是要一个表
示基因的“距离”的合宜的量度。
解 有人提出一种利用向量代数的方法。首先 ,我们用单位向量来表示每一
个群体。为此目的,我们取每一种频率的平方根,记
x
ki
4 4
f
ki
、由于对这四种群体
2
1
、的每一种有
f
ki
1
,所以我们得到
x
ki
这意味着下列四个向量的每个都就
i1 i1
是单位向量、记
x11
x21
x31
x41
x12
x22
x32
x42
, a
3
, a
4
.a
1
, a
2
x13
x23
x33
x43
x14 x24 x34 x44
线性代数在数学建模中的应用举例 2
在四维空间中,这些向量的顶端都位于一个半径为 1 的球面上、
现在用两个向量间的夹角来表示两个对应的群体间的“距离”似乎就是合理
的、如果我们把
a
1
与
a
2
之间的夹角记为θ,那么由于| a
1
|=| a
2
|=1,再由内
只公式,得
cos
a
1
a
2
而
0.5398
0.3216
0.0000
0.2943
, a
2
.a
1
0.1778
0.3464
0.8228
0.8307
故 cos
a
1
a
2
0.9187
得
23.2
°.
按同样的方式,我们可以得到表 1.2.
表 1、2 基因间的“距离”
爱斯基摩人
班图人
英国人
朝鲜人
爱斯基摩人
0°
23、2°
16、4°
16、8°
班图人
23、2°
0°
9、8°
20、4°
英国人
16.4°
9、8°
0°
19.6°
朝鲜人
16、8°
20.4°
19.6°
0°
由表 1、2 可见,最小的基因“距离”就是班图人与英国人之间的“距离”,
而爱斯基摩人与班图人之间的基因“距离”最大、
2 Euler的四面体问题
问题 如何用四面体的六条棱长去表示它的体积?这个问题就是由
Euler(欧拉)提出的、
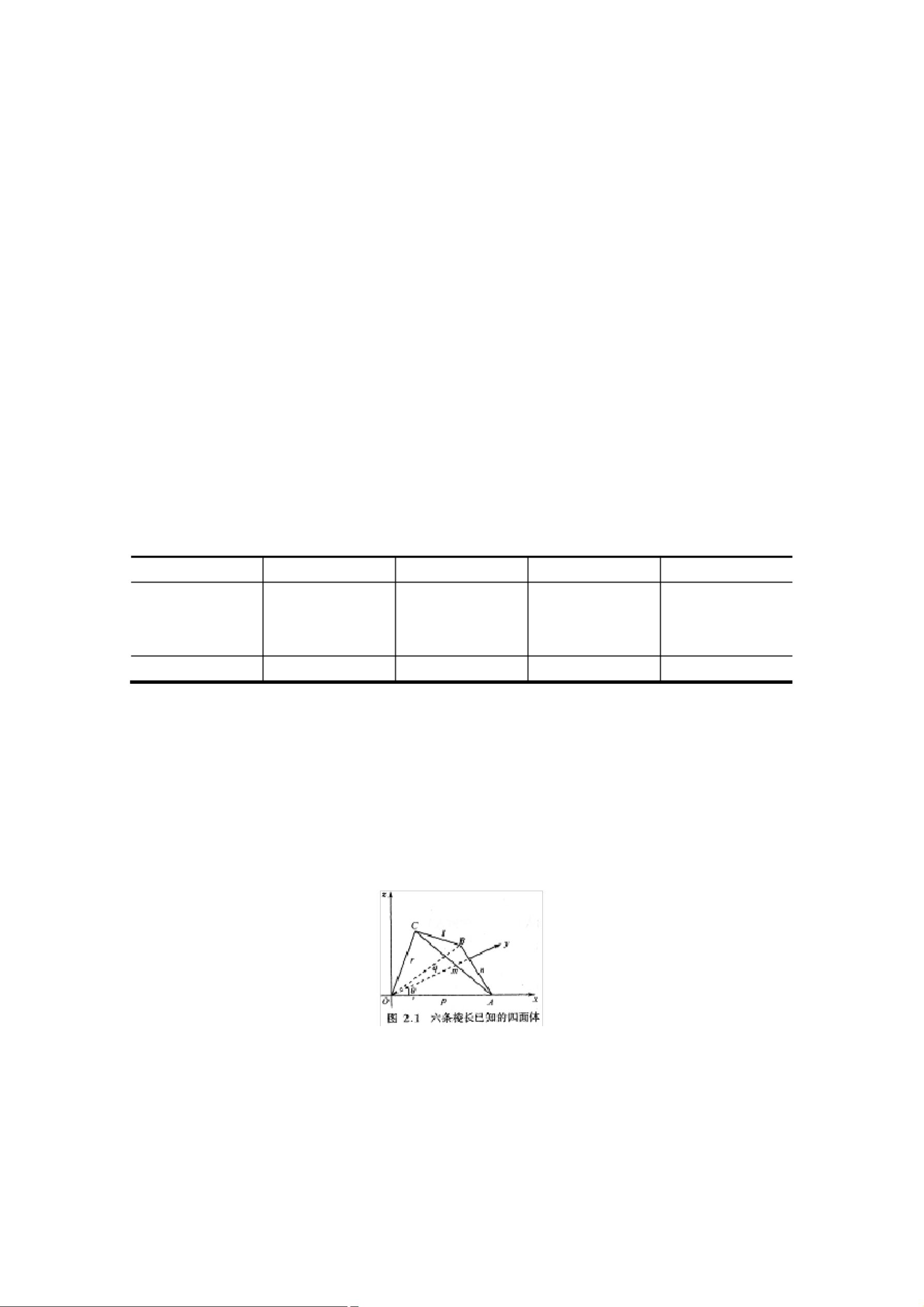
解 建立如图 2、1 所示坐标系,设
A
,
B
,
C
三点的坐标分别为(a
1
,b
1
,c
1
),( a
2
,b
2
,c
2
)
与(a
3
,b
3
,c
3
),并设四面体 O-ABC 的六条棱长分别为
l, m, n, p, q, r.
由立体几何知
道,该四面体的体积V等于以向量
OA,OB,OC
组成右手系时,以它们为棱的平行

线性代数在数学建模中的应用举例 2
1
六面体的体积V
6
的 .而
6
V
6
OA OB OC a
2
a
3
a
1
b
1
b
2
b
3
a
1
b
1
b
2
b
3
c
1
c
1
c
2
.
c
3
于就是得
6V a
2
a
3
将上式平方,得
c
2
.
c
3
a
1
36V
2
a
2
a
3
2
1
b
1
b
2
b
3
2
1
c
1
a
1
c
2
a
2
c
3
a
3
2
1
b
1
b
2
b
3
c
1
c
2
c
3
a
1
a
3
b
1
b
3
c
1
c
3
a
2
a
3
b
2
b
3
c
2
c
3
.
2 2 2
a
3
b
3
c
3
a b c
a
1
a
2
b
1
b
2
c
1
c
2
a
1
a
3
b
1
b
3
c
2
c
3
a
1
a
2
b
1
b
2
c
1
c
2
2 2 2
a
2
b
2
c
2
a
2
a
3
b
2
b
3
c
2
c
3
根据向量的数量积的坐标表示,有
OA OA a
1
2
b
1
2
c
1
2
, OA OB a
1
a
2
b
1
b
2
c
1
c
2
,
2 2 2
OA OC a
1
a
3
b
1
b
3
c
1
c
3
, OB OB a
2
b
2
c
2
2 2
OB OC a
2
a
3
b
2
b
3
c
2
c
3
, OC OC a
3
b
3
2
c
3
.
于就是
OAOA
36V
2
OA OB
OAOB
OB OB
OAOC
OB OC .
(2、1)
OAOC OB OC OC OC
由余弦定理,可行
p
2
q
2
n
2
OAOB p q cos
.
2
同理
p
2
r
2
m
2
q
2
r
2
l
2
OAOC , OB OC .
2 2
将以上各式代入(2、1)式,得

线性代数在数学建模中的应用举例 2
p
2
q
2
n
2
2
p
2
p
2
r
2
l
2
2
p
2
r
2
m
2
2
2
p r
2
l
2
.
(2、2)
2
r
2
p
2
2
p
2
q
2
n
2
36V
2
2
p r
2
m
2
2
这就就是 Euler 的四面体体积公式.
例 一块形状为四面体的花岗岩巨石,量得六条棱长分别为
l
=10m, m=15m, n=12m,
p=14m, q=13m, r=11m、
则
p2 q2 n2
110.5,
2
代入(2、1)式,得
196
36V 2 110.5
46
p2 r2 m2
46,
2
110.5
169
95
46
p2 r2 l2
95.
2
95 1369829.75.
121
于就是
V 2 38050.82639 (195m
3
)
2
.
即花岗岩巨石的体积约为 195m
3
、
古埃及的金字塔形状为四面体 ,因而可通过测量其六条棱长去计算金字塔的
体积、
3 动物数量的按年龄段预测问题
问题 某农场饲养的某种动物所能达到的最大年龄为15 岁,将其分成三个
年龄组:第一组,0~5 岁;第二组,6~10 岁;第三组,11~15 岁、动物从第二年龄组起
开始繁殖后代,经过长期统计,第二组与第三组的繁殖率分别为 4 与3、第一年龄
与第二年龄组的动物能顺利进入下一个年龄组的存活率分别为
错误!
与
错误!
、假设
农场现有三个年龄段的动物各100 头,问15 年后农场三个年龄段的动物各有多
少头?
问题分析与建模 因年龄分组为 5 岁一段,故将时间周期也取为 5 年.15年
后就经过了 3 个时间周期.设
x
i
(k )
表示第
k
个时间周期的第 i 组年龄阶段动物的数
量(
k
=1,2,3;i=1,2,3).
剩余17页未读,继续阅读
资源评论

hhappy0123456789
- 粉丝: 72
- 资源: 5万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功

