线性规划常见题型大全.doc

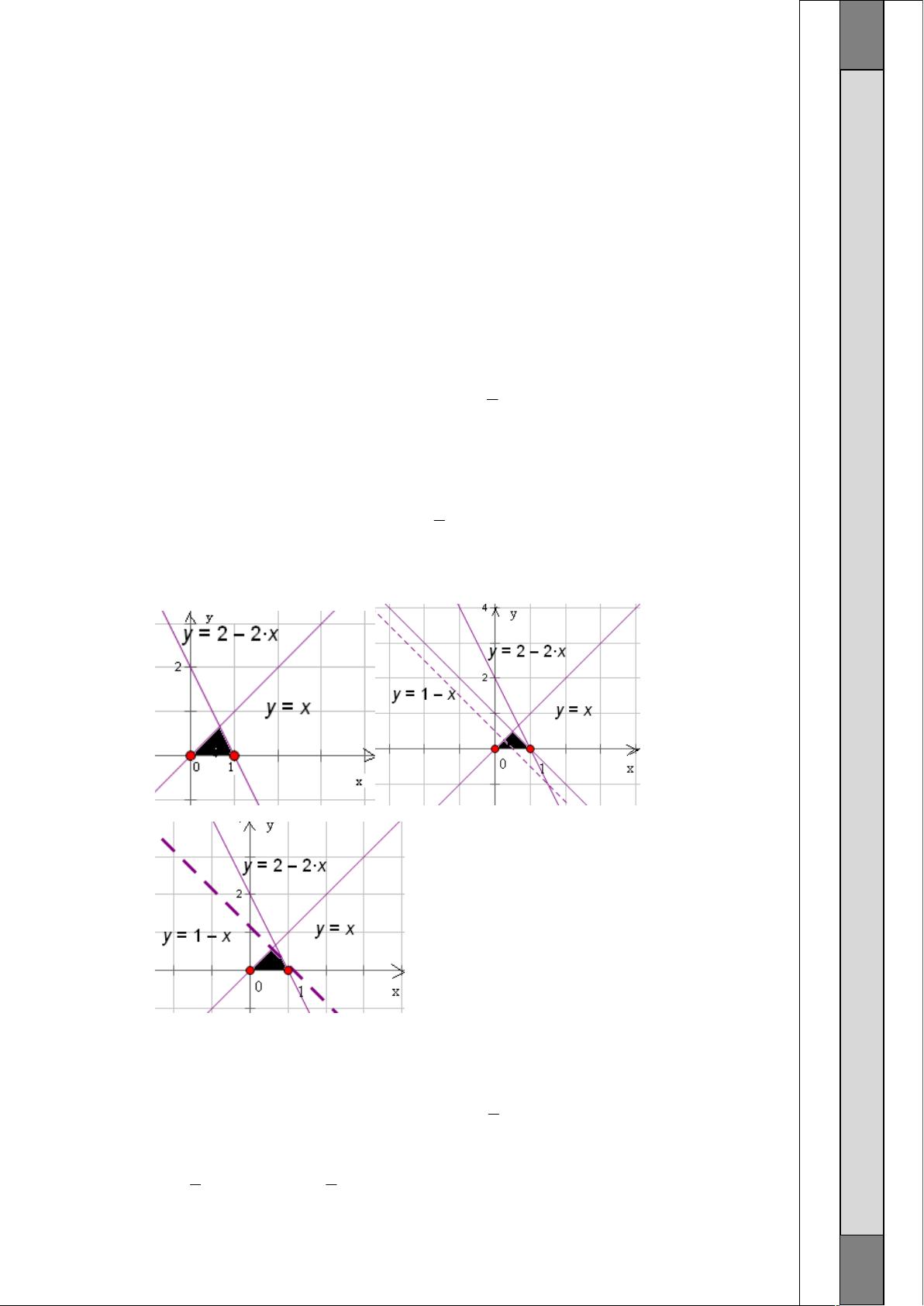
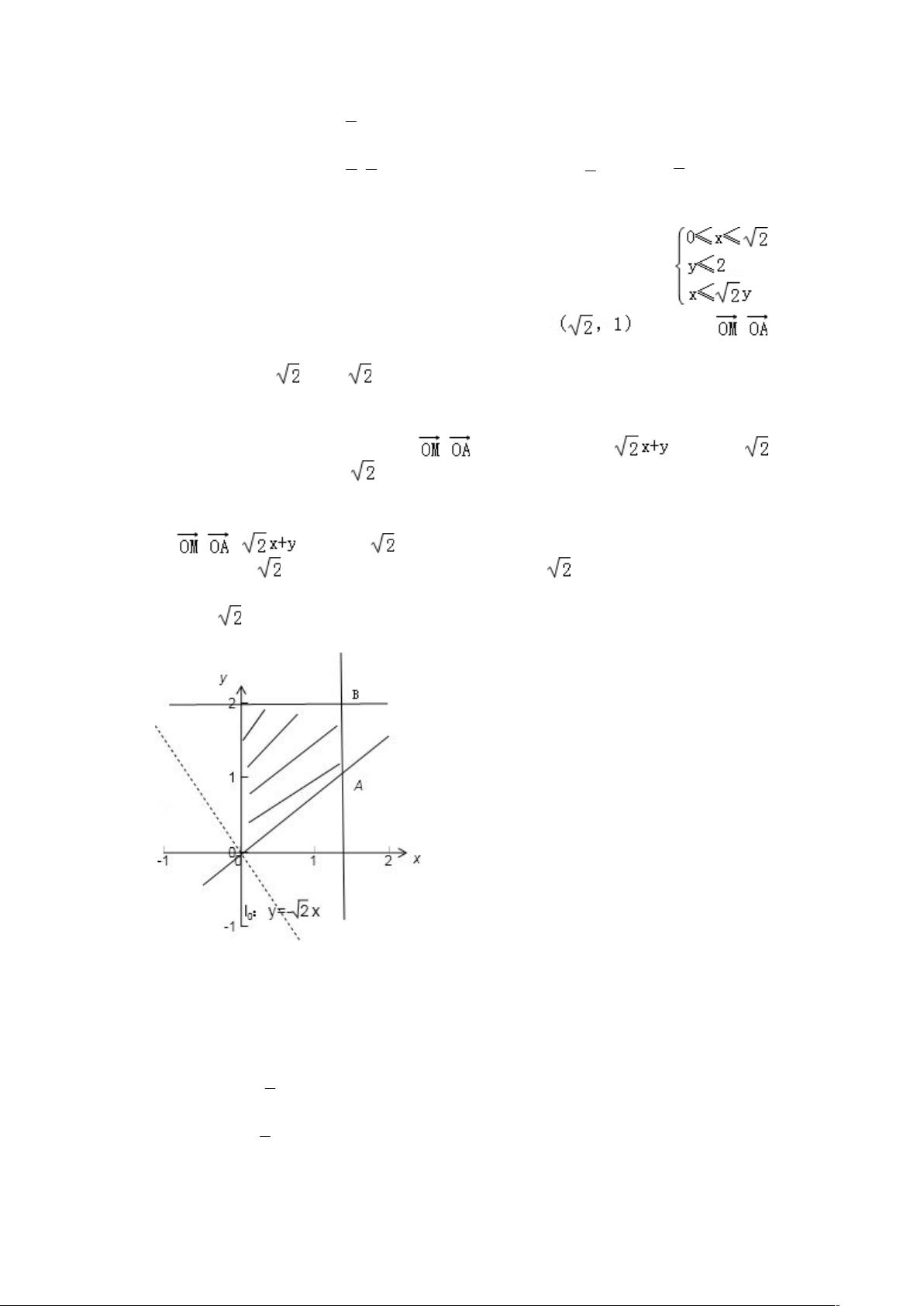
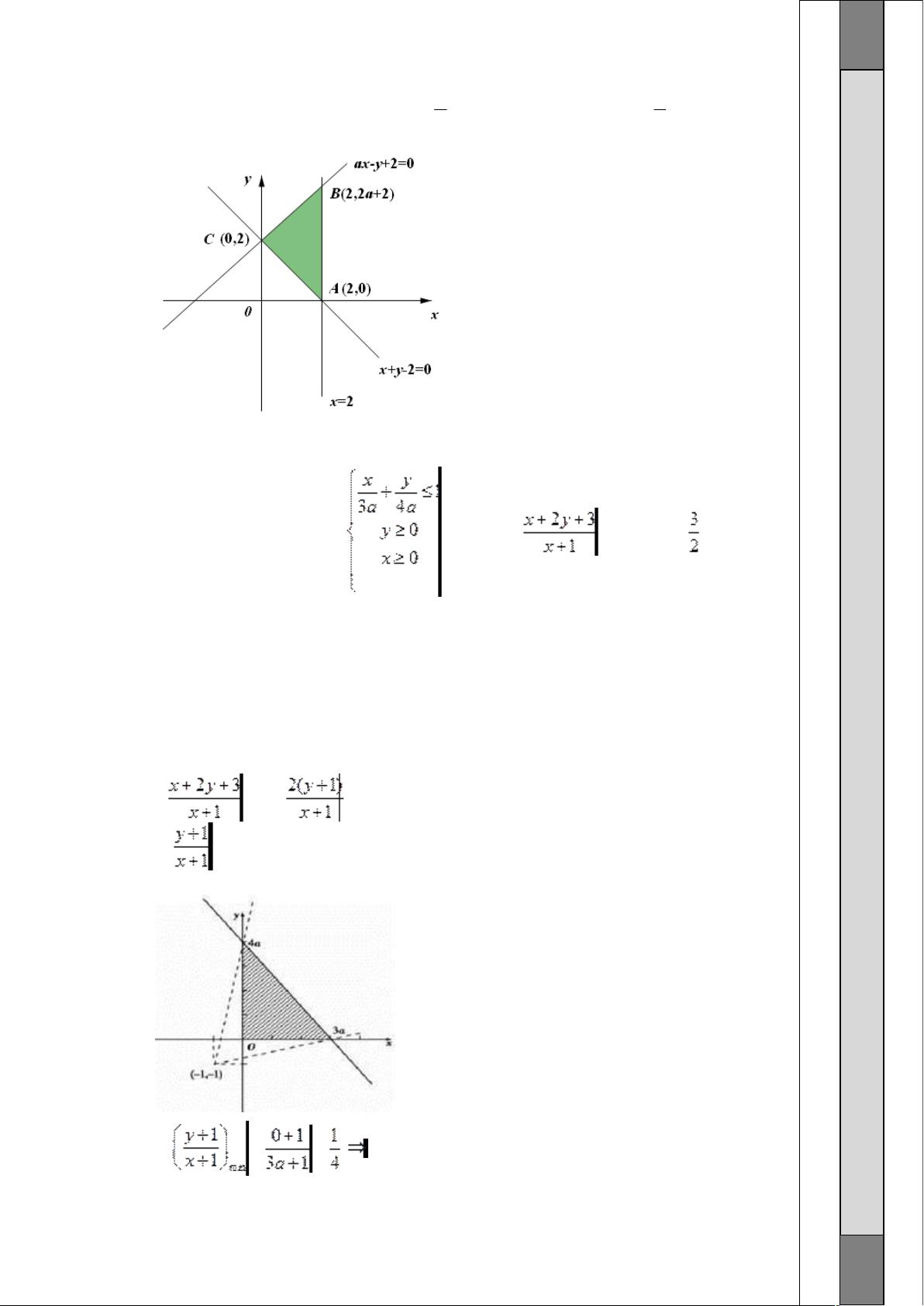
线性规划是一种优化方法，常用于解决在一系列线性不等式约束下的最优化问题，目标是最小化或最大化一个线性目标函数。这个文档，"线性规划常见题型大全.doc"，显然包含了多个线性规划的例题及其解析，帮助学习者理解和掌握线性规划的基本概念和解题技巧。 1. **线性目标函数与可行域**： - 在第一题中，题目要求找到目标函数`z = 4x + y`的最大值。线性规划的解答通常涉及绘制可行域，即满足所有约束条件的点的集合。在这个例子中，通过画出可行域并确定目标函数的最优解，得出当目标函数经过点A(2, 0)时，z取得最大值8。 2. **线性不等式组的几何表示**： - 第二题讨论了不等式组如何决定一个平面区域的形状。不等式组`0 ≤ 2x - y ≤ 2`和`0 ≤ x + y ≤ a`形成的平面区域是三角形，意味着我们需要找到a的取值，使得这个不等式组的解集形成一个三角形区域。通过图形分析，可以得出a的取值范围为`0 < a ≤ 1`或`4/3 ≤ a`。 3. **线性规划与斜率的关系**： - 第三题中，变量x和y满足约束条件`2x + 70y ≥ 0`, `-1 ≤ x - y ≤ 0`，题目要求求解`y/x`的取值范围。这里的`y/x`可以看作可行域内的点与原点连线的斜率。通过分析可行域及其边界，可以确定斜率`y/x`的取值范围是`[5/9, 6)`。 4. **向量和线性规划的结合**： - 第四题将线性规划与向量的坐标表示结合，要求找出向量`M(x, y)`与固定点`A`的乘积`z = MA`的最大值。解题策略是将向量乘积转化为直线的斜率形式，然后通过移动这条直线找到其与可行域相交并使z达到最大值的点。 5. **线性不等式组的面积**： - 最后一题涉及到不等式组`2x + 2y - ax ≥ 0`, `x - y ≥ 0`, 和 `2x - y ≥ 0`表示的平面区域面积。通过解不等式组，我们可以得到平面区域的边界，然后计算这个区域的面积来确定a的值。 这些题目展示了线性规划的核心概念，包括建立线性模型，画出可行域，以及确定目标函数的最优解。它们也强调了利用图形分析在解决线性规划问题中的重要性。通过解决这类问题，学生可以提升对线性规划理论的理解，并掌握实际应用中的技巧。