nonlinear_least_squares

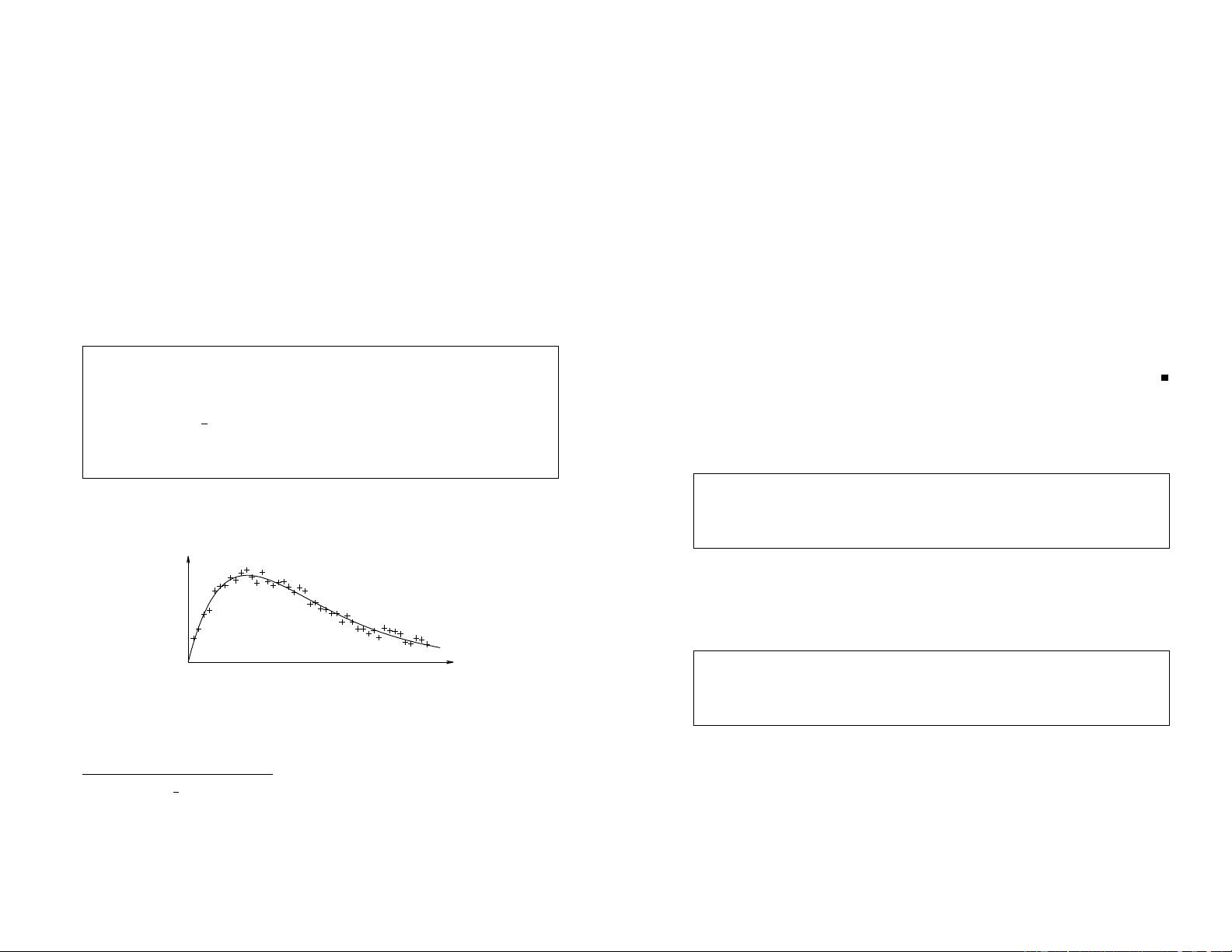
非线性最小二乘法是一种数学优化技术，用于解决非线性模型中参数的估计问题。当模型的输出与数据之间存在误差时，最小二乘法通过最小化误差的平方和来寻找最佳参数。这种方法广泛应用于各种领域，如统计、数据拟合、信号处理、工程设计以及经济学等。 非线性最小二乘问题通常难以解析求解，因此需要采用迭代算法进行求解。文中提到了基于导数的最优算法，包括梯度下降法、牛顿法、线搜索法、信赖域法以及阻尼法等。 梯度下降法是一种最基本的优化算法，它通过迭代的方式来更新参数。在每次迭代中，参数沿着负梯度方向进行更新，即向使目标函数值减少的方向移动。这个过程持续进行，直到达到局部最小值或满足停止准则。牛顿法是一种二阶优化算法，它利用函数的二阶导数（海森矩阵）信息来进行参数更新。牛顿法的迭代公式考虑了目标函数的曲率，因此往往比梯度下降法更加迅速。牛顿法的一个缺陷是需要计算和存储二阶导数，这在高维问题中可能会成为计算负担。 线搜索法是一种在每次迭代中寻找一个合适步长的方法。在确定了方向之后，线搜索算法试图找到一个最佳的步长，使得目标函数在该方向上下降最多。信赖域法是另一种迭代优化技术，它通过限制解的更新步长在某个“信赖域”内来保证算法的稳定性和收敛性。信赖域的大小随着迭代过程进行而动态调整。阻尼法是牛顿法的一种变体，它通过引入阻尼因子来减小更新步长，从而在保证算法稳定性的同时避免目标函数值的大幅度波动。 文档还提到了用于解决非线性最小二乘问题的几种特定算法，包括高斯-牛顿法、列文伯格-马夸特法、鲍威尔的犬腿法、L-M法和拟牛顿法的混合方法，以及L-M法和犬腿法的割线版本。 高斯-牛顿法是解决非线性最小二乘问题的常用方法，尤其适用于模型误差接近正态分布的情况。它利用雅可比矩阵（即误差函数的梯度矩阵）来线性化模型。当问题接近线性时，高斯-牛顿法效率较高，但如果模型非常非线性，算法可能无法收敛。 列文伯格-马夸特法是对高斯-牛顿法的改进，它在牛顿法的基础上增加了阻尼因子，以提高算法的鲁棒性。当模型函数在当前参数值附近的线性化不足以保证收敛时，列文伯格-马夸特法特别有效。 鲍威尔的犬腿法是一种特殊方法，用于在参数空间中搜索最小二乘解。它结合了高斯-牛顿法和梯度下降法，以避免搜索过程中出现的过度步长。 L-M法是一种结合了梯度下降法和高斯-牛顿法的算法，通过引入一个阻尼因子来平衡这两者的优点。L-M法在处理非线性问题时更加稳定，尤其是当问题非常非线性时。 拟牛顿法是一类利用目标函数的梯度信息来构建一个近似海森矩阵的优化方法。在L-M法和拟牛顿法的混合方法中，两种算法的优势被结合起来，以期望获得更好的优化性能。 文档最后提到了这两种割线版本方法的改进形式，割线法是一种不需要计算二阶导数（海森矩阵）的优化算法，它通过使用前两次迭代的信息来估计梯度，从而降低计算成本。 这些方法的选择和使用通常取决于具体问题的特性，如问题的规模、是否多峰、梯度信息的可用性以及计算资源等。非线性最小二乘法以及相关算法是数据分析、科学计算和工程领域中不可或缺的工具，它们对于从复杂数据中提取有价值信息至关重要。