双因素方差分析是一种统计方法,用于检验两个独立变量(因素A和因素B)对一个连续因变量的影响。在第四章的讲解中,主要聚焦于双因素无重复和等重复两种情况。
一、双因素无重复方差分析
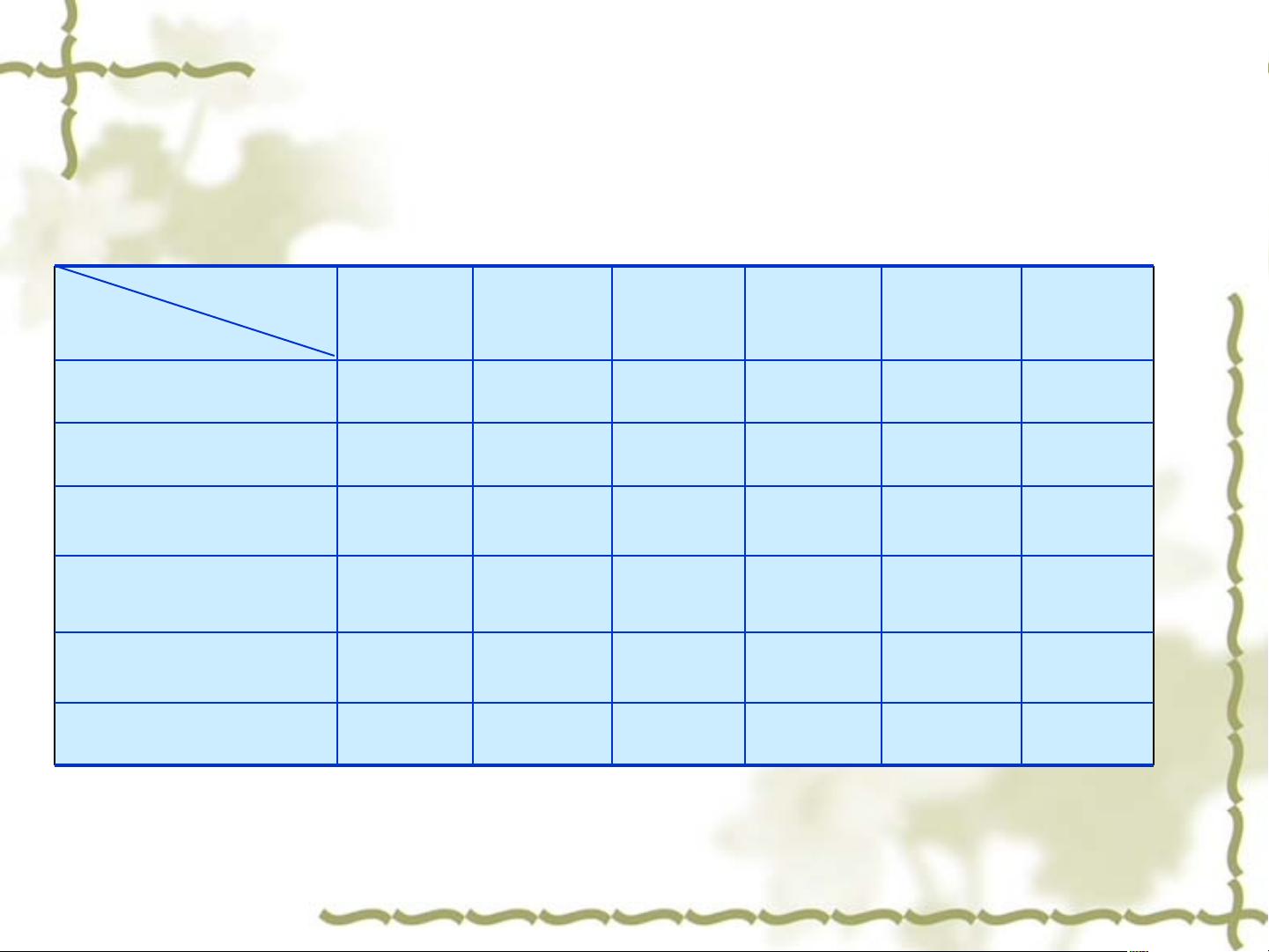
在双因素无重复方差分析中,数据通常以表格形式呈现,如表4.1所示。每个处理组合(A水平和B水平的交叉)只有一个观测值,这意味着实验不会在同一条件下重复。例如,A1B1表示因素A的第一水平与因素B的第一水平的组合,对应的观测值是y11。这样的数据结构有助于分析两个因素的单独效应以及它们之间的交互效应。
二、平方和与自由度的分解
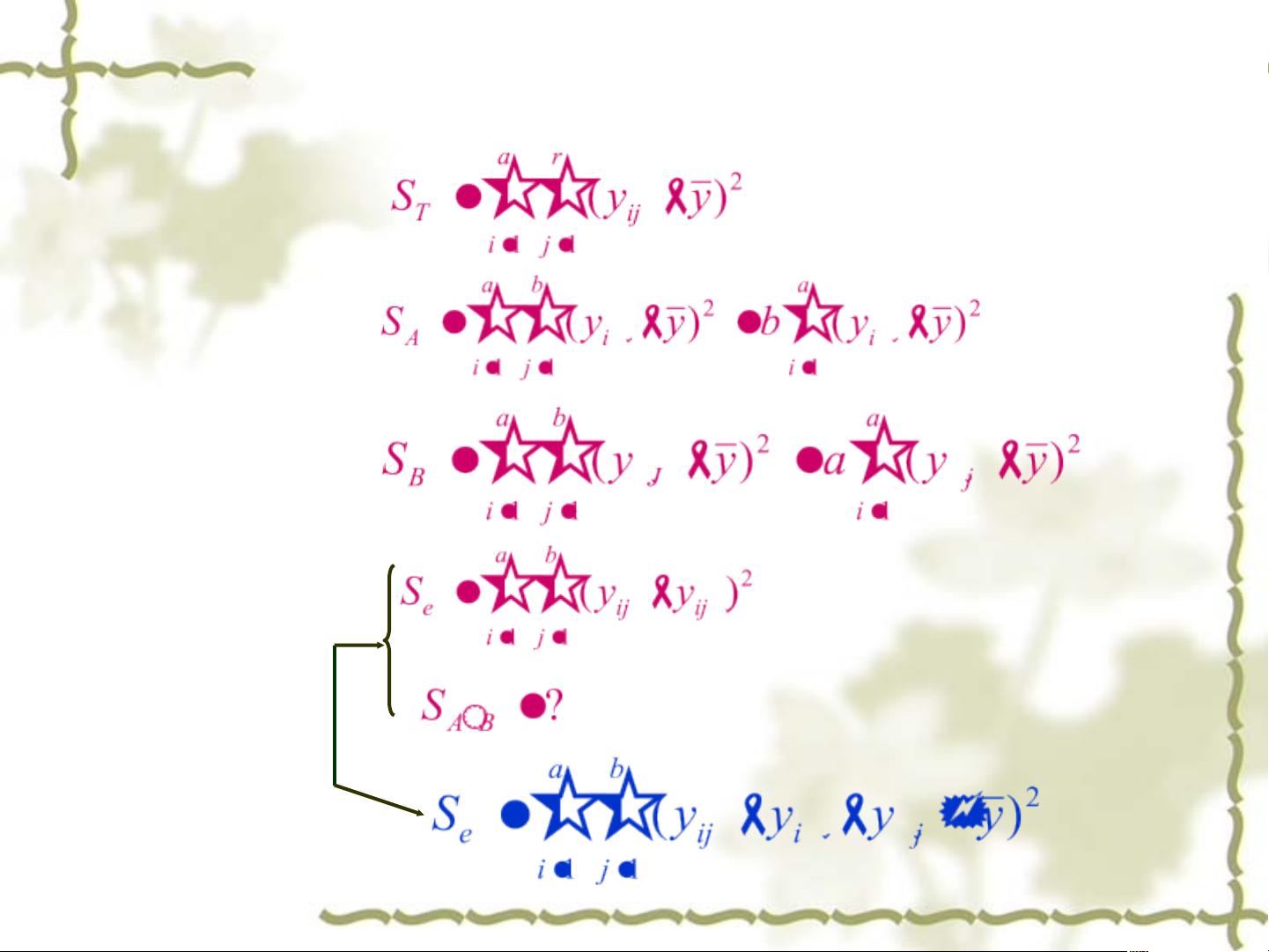
在方差分析中,总偏差被分解为几个部分,包括因素A的偏差平方和、因素B的偏差平方和、因素A与B交互影响的偏差平方和以及试验误差。这些平方和代表了不同来源的变异。自由度分析则用于确定每部分的自由度,比如因素A的自由度是a-1,因素B的自由度是b-1,交互作用的自由度是(a-1)(b-1),以及误差的自由度。
三、简化计算与F值
通过计算各平方和的自由度和均方(方差),可以得到F统计量,它是一个比较因素效应与随机误差比例的指标。F值等于某一平方和的均方除以误差平方和的均方。通过比较F值与特定显著性水平下的F分布临界值,我们可以判断因素A和B的影响是否显著。例如,在例4.3中,如果F值大于临界值,我们就可以拒绝原假设,认为因素A对纯度有显著影响,而如果F值小于临界值,则因素B的影响不显著。
四、双因素等重复方差分析
在双因素等重复方差分析中,每个处理组合有多个重复观测,这允许我们对每个因素的均值进行更准确的估计,同时考虑测量误差。这种分析方式特别适用于实验条件可以重复的情况下,比如实验中的随机误差可以通过多次测量来平均。
总结来说,双因素方差分析是探究两个独立变量对一个响应变量联合影响的有效工具。无重复和等重复两种类型根据实验设计的不同而选择。通过计算和比较平方和、自由度、F值以及进行假设检验,我们可以确定每个因素的显著性,并理解它们如何共同影响结果变量。在实际应用中,这种方法广泛应用于科学、工程、医学和社会科学等领域,以揭示复杂的因果关系。