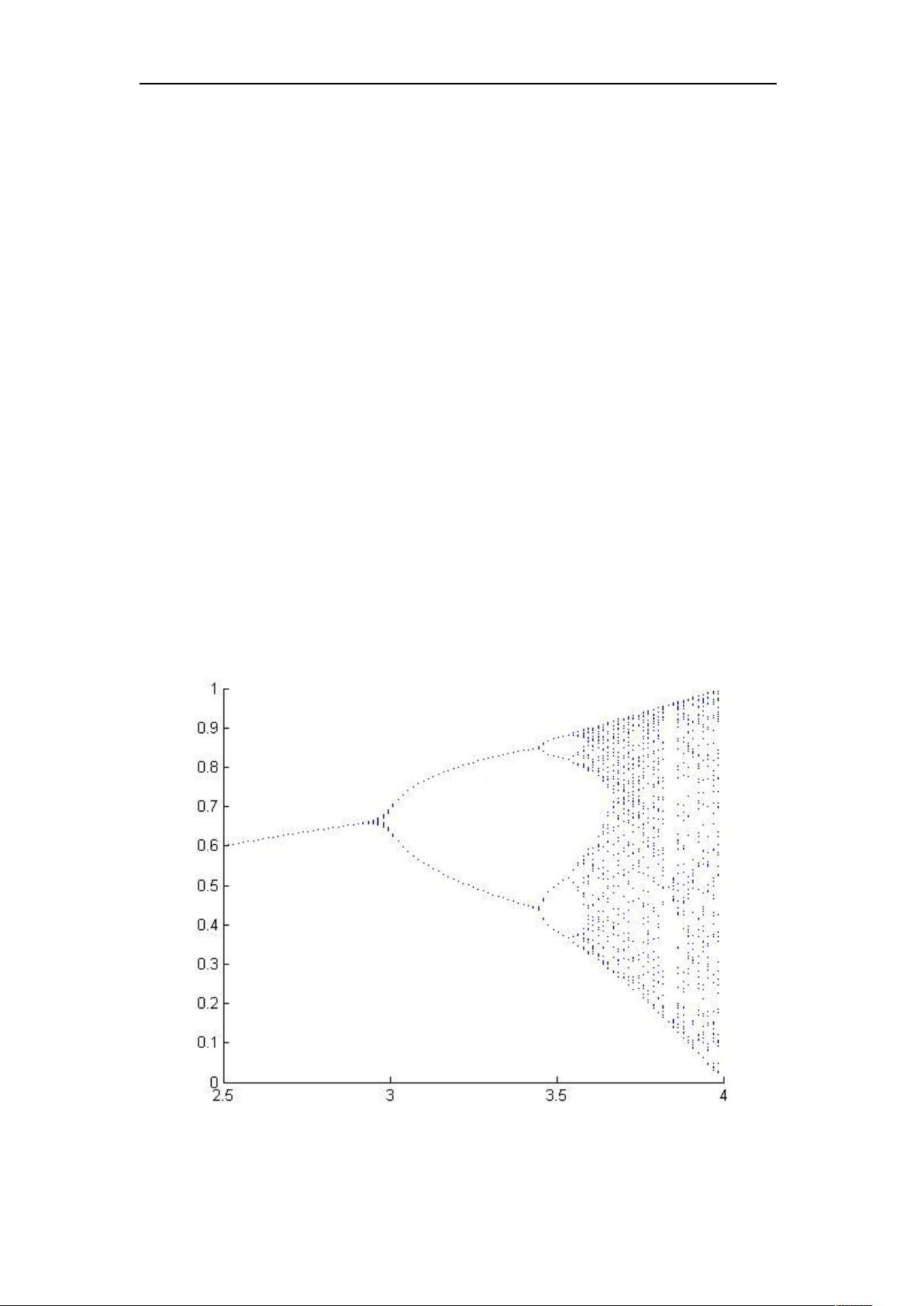
差分形式的阻滞增长模型是一种在生物学、经济学和物理学等多个领域广泛应用的动态系统模型，它用来描述系统在受到内外因素影响时的增长规律。在这个模型中，x(n) 表示系统在第 n 个时间步的状态，b 是一个参数，反映系统内部的自我调节能力。模型的核心在于它的非线性特性，即增长速率依赖于当前状态 x(n-1) 和其前一步 x(n-2) 的乘积。
模型的方程式是：
x(n) = bx(n-1)(1 - x(n-1))
这个方程揭示了系统的一个关键特性：当 x(n-1) 接近 0 或 1 时，增长会受到抑制（阻滞），因为此时增长因子 b(1-x(n-1)) 接近于 0。这种现象在自然界中很常见，比如种群数量达到环境承载力时的增长限制。
在数学上，研究差分形式的阻滞增长模型通常涉及以下几个方面：
1. **收敛性**：研究模型是否趋于某个稳定状态，即 x(n) 随着 n 的增加是否会收敛到某个常数值。这可以通过分析系统的平衡点（x'(n) = 0 的解）以及它们的稳定性来完成。
2. **分岔**：当参数 b 改变时，系统的动态行为可能发生变化，出现新的稳定点或不稳定点，这就是分岔。分岔理论可以帮助我们理解系统从有序到混沌的转变。
3. **混沌**：在某些参数条件下，阻滞增长模型可能出现混沌行为，即系统对初始条件极其敏感，长期预测变得几乎不可能。混沌是复杂系统的一个重要特征，常常与“蝴蝶效应”相联系。
在 MATLAB 环境下，我们可以编写函数 fun.m 来模拟这个模型，并利用混沌分析工具如 Lyapunov 指数或 Poincaré 平面来探索系统的动态行为。例如，`fun.m` 可能包含以下代码：
```matlab
function x = fun(x0, b, steps)
x = zeros(steps, 1);
x(1) = x0;
for n = 2:steps
x(n) = b*x(n-1)*(1 - x(n-1));
end
end
```
通过调用这个函数并绘制结果，我们可以得到模型的迭代轨迹，进一步分析其收敛性、分岔和混沌特性。文档混沌.doc可能包含了具体的 MATLAB 实现细节和分析结果。
差分形式的阻滞增长模型是一个强大的工具，用于描述具有内在自我调节机制的系统的动态行为。通过深入研究，我们可以理解系统的稳定状态、分岔现象以及混沌行为，这些对于理解和预测复杂系统的行为至关重要。
