游戏算法整理(贴图完整版)
游戏算法在游戏开发中扮演着至关重要的角色,特别是在游戏中的寻路系统中。A*(A Star)寻路算法是一种广泛应用的高效路径寻找算法,它广泛用于策略游戏、角色扮演游戏和实时战略游戏中,帮助游戏中的角色或玩家找到从起点到终点的最短路径。 A*算法的核心思想是通过评估每个节点的总成本(F值)来决定下一个要探索的节点。F值由两部分组成:G值和H值。G值代表从起点到当前节点的实际代价,而H值则是从当前节点到目标节点的预估代价。这种预估代价的计算方法称为启发式函数,通常基于曼哈顿距离或欧几里得距离,但在实际应用中可以根据游戏世界的具体规则进行调整。 在游戏环境中,地图通常被划分为网格,每个网格节点代表一个可通行或不可通行的位置。A*算法首先将起点加入开启列表,然后逐步将相邻的可通行节点加入,同时记录它们的父节点(即上一个被访问的节点)。每次从开启列表中选择F值最低的节点进行扩展,将其移出开启列表并加入关闭列表,表示这些节点不再需要被考虑。 在计算G值时,考虑到游戏中的移动规则,通常假设水平和垂直移动成本相同,对角线移动成本为水平或垂直移动成本的平方根,以保持曼哈顿距离的合理性。例如,如果水平和垂直移动成本为1,则对角线移动成本为约1.414。 H值的计算是启发式的一部分,它的目的是估计从当前节点到目标节点的剩余距离。常见的启发式函数有曼哈顿距离(直线距离,忽略障碍物)和欧几里得距离(考虑障碍物的直线距离)。在实际应用中,还可以根据游戏世界的特性设计更复杂的启发式,如切比雪夫距离或者其他更精确的预估方法。 在A*算法的迭代过程中,每当选择新的节点时,算法会更新所有相邻节点的F值,以反映通过新路径到达它们的成本。这一过程持续直到目标节点被添加到关闭列表,此时,通过回溯父节点,就可以构建出从起点到目标的最短路径。 游戏开发者通常会使用不同的编程语言实现A*算法,如C++或Blitz Basic,甚至会有现成的库供开发者调用。为了优化性能,还可以使用数据结构如优先队列(如二叉堆)来存储和检索开启列表中的节点。 A*算法在游戏寻路中的应用使得游戏世界中的角色能够智能地导航,避开障碍,找到最佳路径。理解和掌握A*算法对于游戏开发人员来说是必不可少的技能,它不仅提高了游戏体验,也为游戏世界增加了真实感和沉浸感。通过不断学习和实践,开发者可以针对特定的游戏场景进一步优化和调整A*算法,以达到最佳的寻路效果。


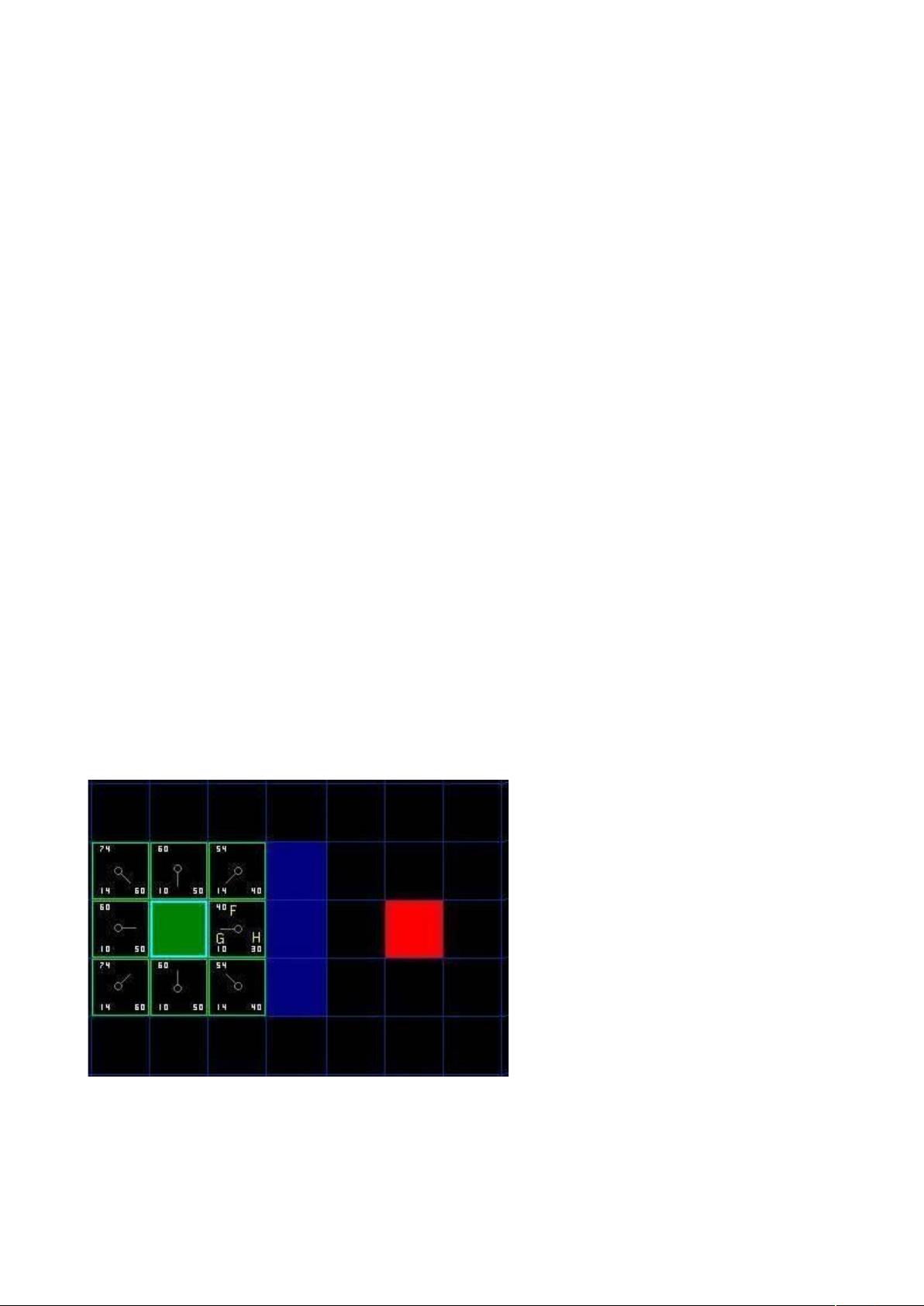
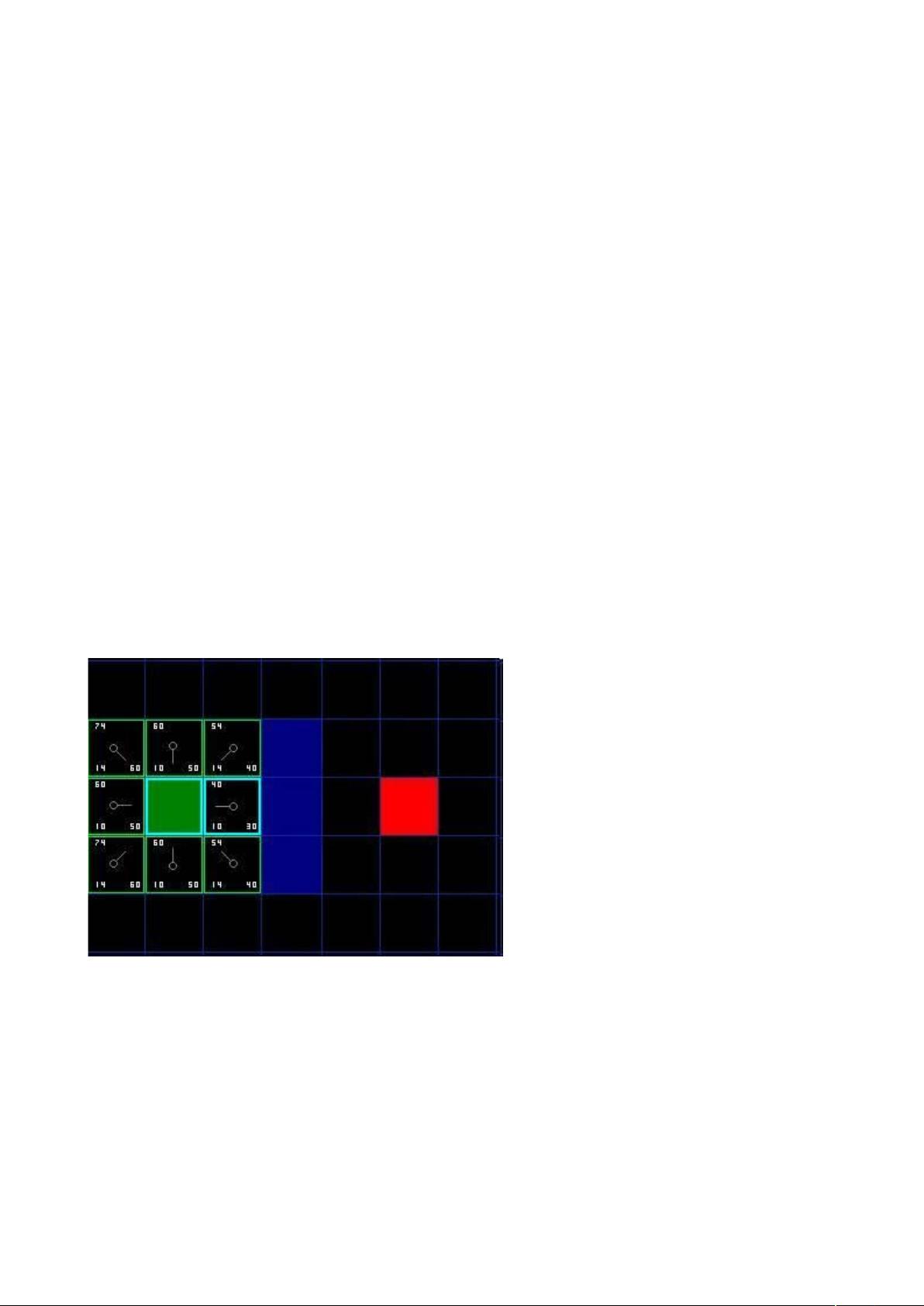
剩余25页未读,继续阅读

 flcode2014-02-08文章不错,如果能详细的给出一个例子那就好多了!
flcode2014-02-08文章不错,如果能详细的给出一个例子那就好多了!
- 粉丝: 0
- 资源: 1
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功