二阶电路的动态响应[整理].pdf

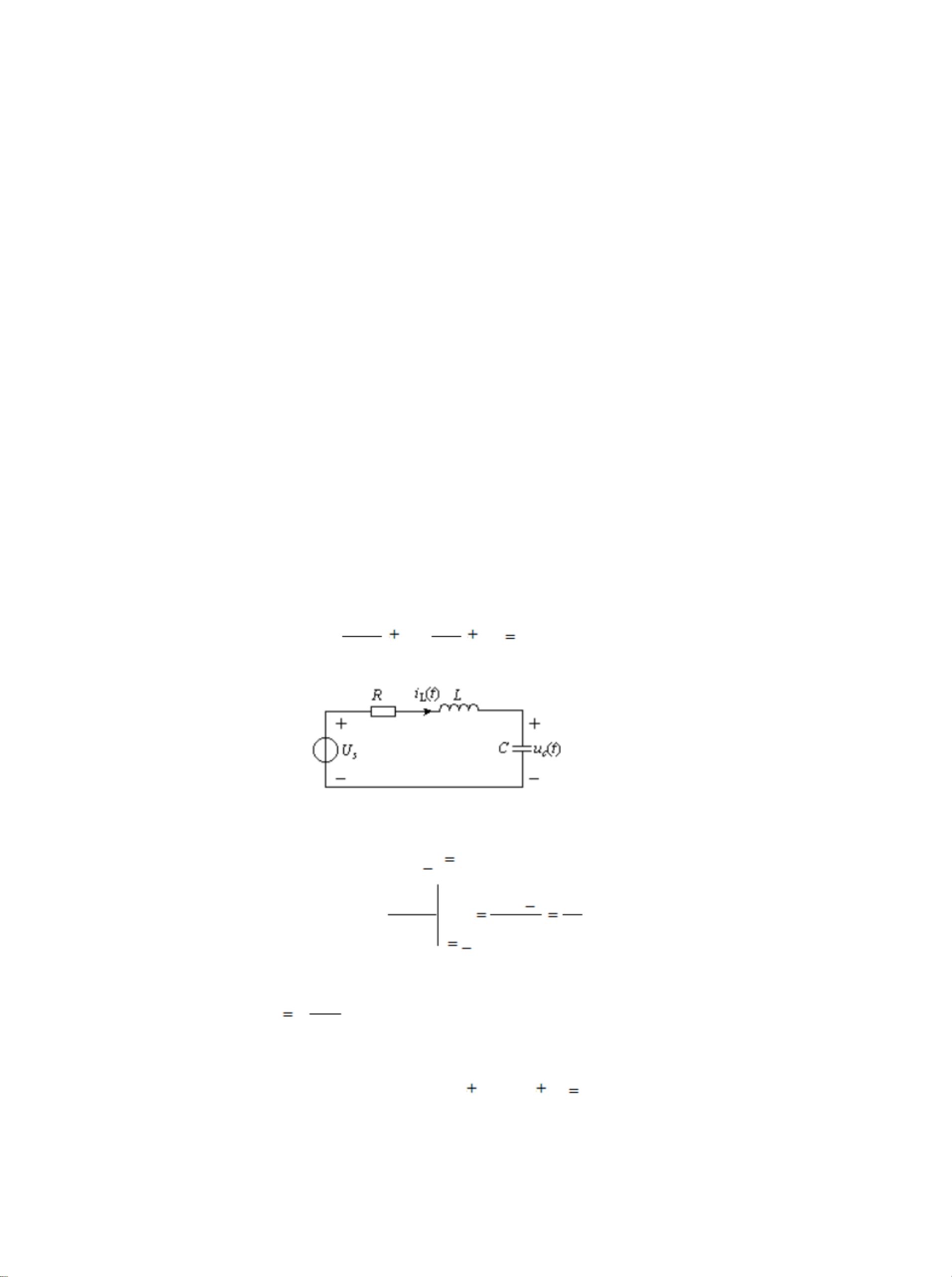
二阶电路的动态响应是电子工程领域中的一个重要概念，尤其在软件开发中，理解电路的动态行为对于设计高效能的电路系统至关重要。二阶电路，正如其名，是由至少一个电容（C）和一个电感（L）组成的电路，它们共同决定了电路的动态特性。这类电路通常可以被描述为一个二阶线性常系数微分方程，用于分析电路的瞬态响应。 在本实验中，我们关注的是二阶电路的动态响应，即电路在受到外部激励或内部储能影响时的行为。实验目标包括学习如何通过实验研究动态响应，探讨元件参数如何影响电路的响应，并具体研究阻尼系数和固有频率等参数。 二阶电路的微分方程可以表示为s^2U + sUC + UL = 0，其中s是复数频率，U是电容上的电压，Uc和Ul分别表示电容和电感两端的电压，C和L分别是电容和电感的值，R是电路的总电阻。这个方程的特征根是两个实数或一对共轭复数，它们定义了电路的响应类型。 1. **零输入响应**：当没有外部激励时，电路响应由初始储能引起。根据阻尼系数α和固有频率ω0，零输入响应可以分为三种情况： - 过阻尼（α > ω0）：响应是非振荡性的，电压和电流逐渐减少至零。 - 临界阻尼（α = ω0）：响应没有振荡，电压和电流快速减小至零。 - 欠阻尼（α < ω0）：响应包含振荡，电压和电流会在衰减至零前振荡一段时间。 2. **零状态响应**：当电路初始储能为零，仅由外部激励引起响应。零状态响应同样受到阻尼系数和固有频率的影响，表现为不同类型的充电过程。 3. **状态轨迹**：电路的状态可以通过两个一阶微分方程描述，这些方程的解形成了状态轨迹，反映了电压和电流随时间变化的路径。 实验中使用了Multisim进行仿真，通过改变电阻值来模拟不同的阻尼条件，观察并记录了过阻尼、临界阻尼和欠阻尼状态下的电路响应。此外，实际焊接的电路也进行了测量，比较了理论计算与实际测量之间的差异，以进行误差分析。实际电路中的电感电阻和电容器的介质损耗会影响理想状态，导致实际阻尼状态与理论计算有所偏差。 在分析电路响应时，还应注意振荡周期Td、峰值h1和h2以及衰减率α等参数。这些参数可以帮助我们更深入地理解电路动态响应的性质，从而优化电路设计。在软件开发中，这些知识可用于模拟和预测电路行为，以确保系统的稳定性和效率。