在数学建模中,MATLAB 是一个非常强大的工具,它提供了丰富的函数和运算符来处理各种复杂的数学问题。以下是一些常用地MATLAB程序和函数的详细解释:
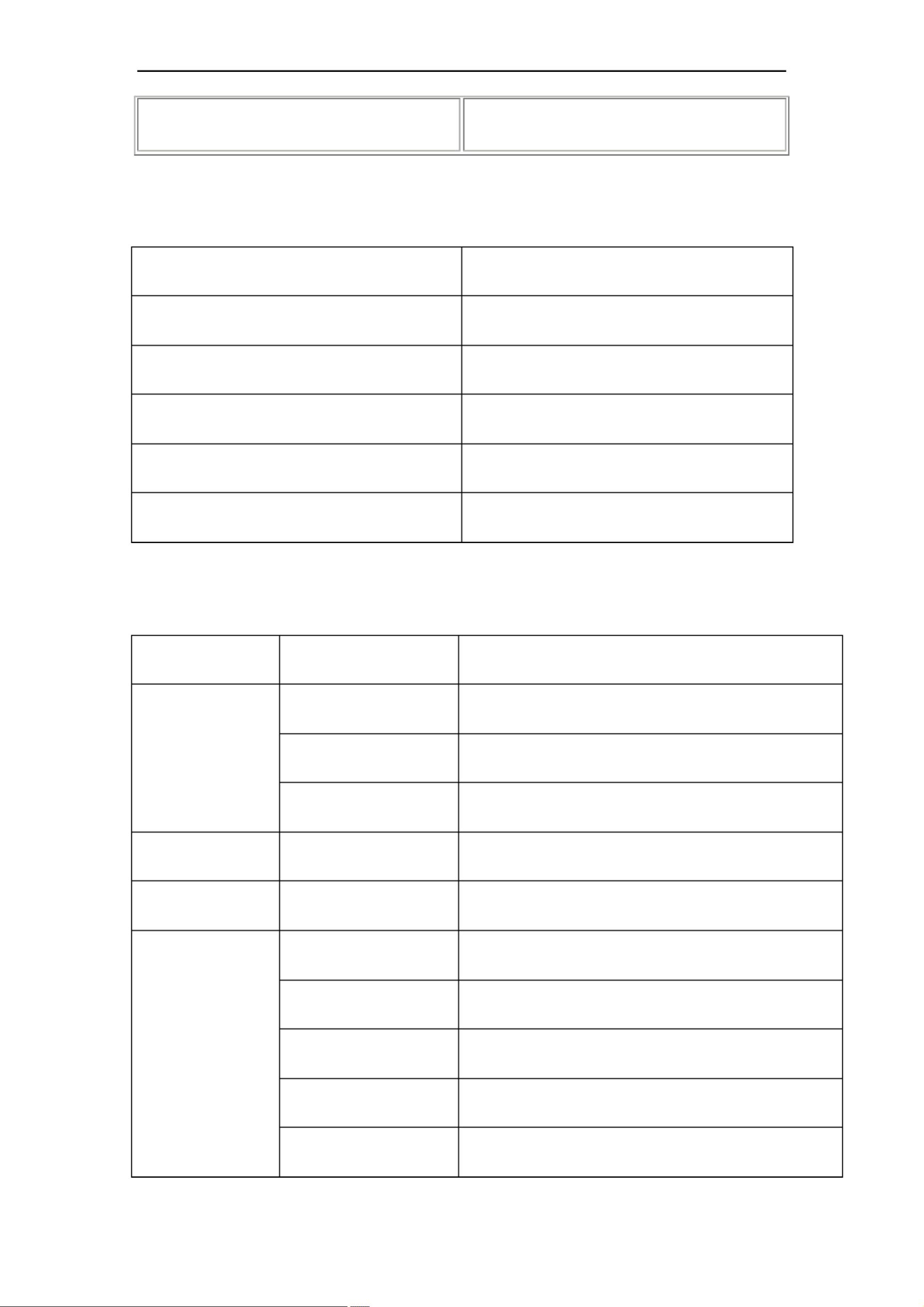
1. **数学常数**:
- `pi`:表示圆周率 π。
- `exp(1)`:计算自然对数的底数 e。
- `i` 或 `j`:代表复数的虚部单位。
- `Inf` 或 `inf`:表示无穷大。
2. **基本数学运算符**:
- `+`,`-`,`*`,`./`,`.\`,`^`:分别用于加法、减法、乘法、元素-wise除法(右除和左除)以及乘方运算。
- `.*` 和 `./`:用于数组乘法和除法,每个元素都执行运算。
- `\` 和 `/`:矩阵除法,前者是右除,后者是左除。
- `^` 和 `.^`:矩阵乘方和元素-wise乘方。
3. **关系运算符**:
- `==`,`<`,`>`,`<=`,`>=`,`~=`:用于比较操作,分别表示等于、小于、大于、小于等于、大于等于和不等于。
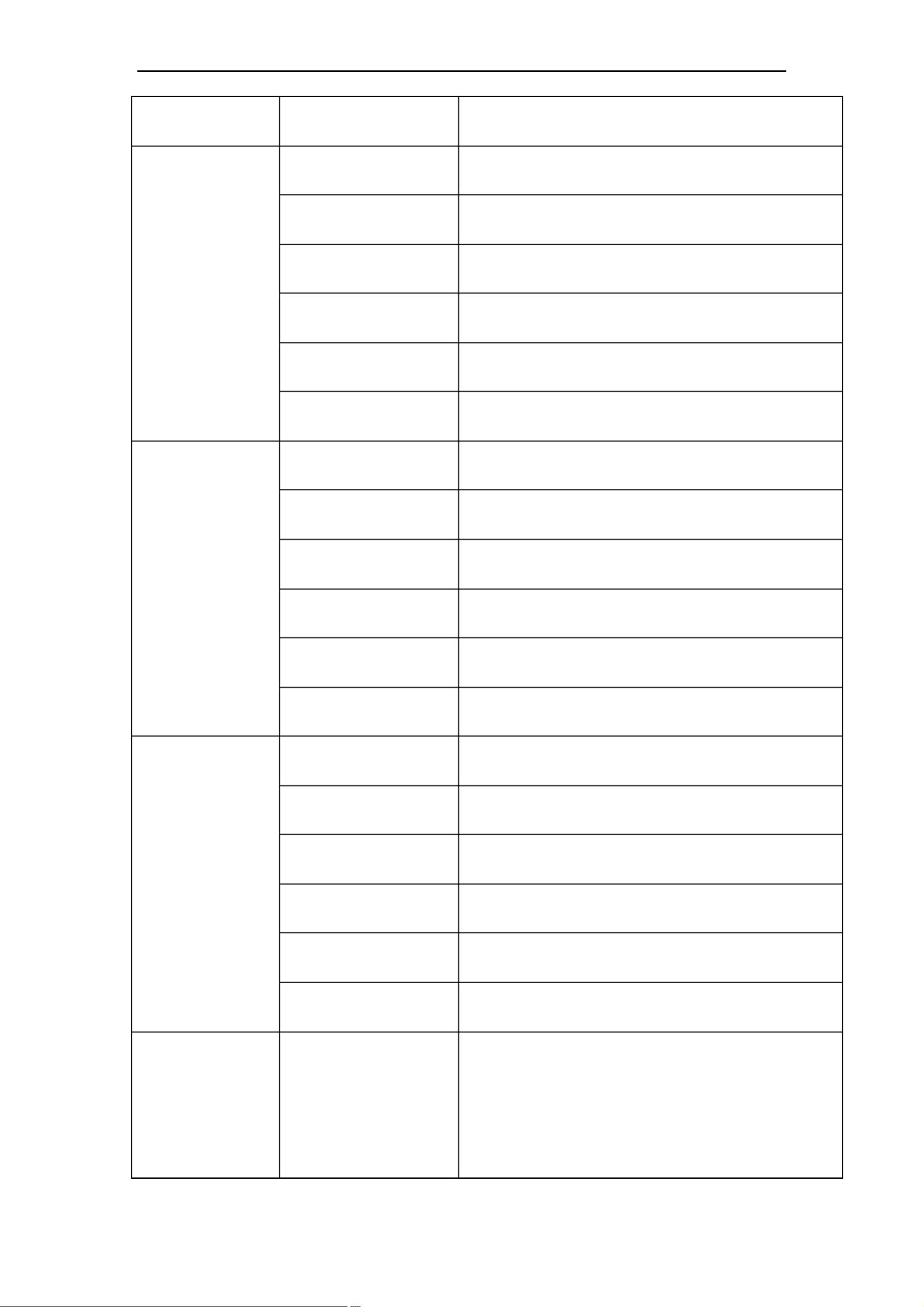
4. **常用内部数学函数**:
- `exp(x)`:计算 e 的 x 次方。
- `log(x)`:以 e 为底的对数。
- `log10(x)`,`log2(x)`:以 10 和 2 为底的对数。
- `sqrt(x)`:平方根。
- `abs(x)`:绝对值。
- `sin(x)`, `cos(x)`, `tan(x)`, `cot(x)`, `sec(x)`, `csc(x)`:正弦、余弦、正切、余切、正割和余割,这些函数接受弧度作为输入。
- `asin(x)`, `acos(x)`, `atan(x)`, `acot(x)`, `asec(x)`, `acsc(x)`:它们是对应的反三角函数。
- `sinh(x)`, `cosh(x)`, `tanh(x)`, `coth(x)`, `sech(x)`, `csch(x)`:双曲函数。
- `asinh(x)`, `acosh(x)`, `atanh(x)`, `acoth(x)`, `asech(x)`, `acsch(x)`:反双曲函数。
5. **数论和组合函数**:
- `gcd(a,b)`:计算最大公约数。
- `lcm(a,b)`:计算最小公倍数。
- `factorial(n)`:n的阶乘。
- `real(z)`,`imag(z)`:复数的实部和虚部。
- `abs(z)`,`angle(z)`,`conj(z)`:复数的模、幅角和共轭。
6. **自定义函数**:
- 使用 `function` 关键字定义函数,例如 `function 返回变量=函数名(输入变量)`,在函数体中实现特定的计算逻辑。
7. **函数的复合运算**:
- `compose(f,g)`,`compose(f,g,z)`,`compose(f,g,x,y,z)`:分别表示 f(g(y)),f(g(z)) 和 f(g(z)) 的复合运算。
8. **因式分解**:
- `factor(表达式)`:将表达式因式分解。
9. **代数式展开**:
- `expand(表达式)`:展开表达式中的乘积和指数。
10. **合并同类项**:
- `collect(表达式,指定的变量)`:按照指定变量将同类项合并。
11. **数学式化简**:
- `simplify(表达式)`:对表达式进行简化。
12. **变量替换**:
- `subs(表达式,要替换的变量或式子,代换式)`:将表达式中的某些变量或式子替换为指定的代换式。
13. **数学式转换**:
- `maple(‘转换命令')`:利用 Maple 的功能将表达式转换成特定形式。
14. **解方程**:
- `solve(’方程’,’变元’)`: 解单个方程,等号使用普通等号 `=`。
15. **解不等式**:
- `maple('maple 中解不等式的命令')`:调用 Maple 解不等式,有多种格式,根据需求选择。
16. **解不等式组**:
- `maple('maple 中解不等式组的命令')`:解决一组不等式,同样需要调用 Maple 的相应命令。
这些函数和运算符在MATLAB中广泛应用于数学建模,无论是数值计算、符号计算还是图形绘制,都能提供极大的便利。掌握这些基础工具,能帮助我们更高效地解决数学模型中的问题。