最大似然估计与最大后验估计 最大似然估计(Maximum Likelihood Estimation,MLE)是一种统计学方法,用于估计模型参数。它的基本思想是:给定观察数据,找出使该数据出现的概率最大的模型参数。MLE 方法的优点是简单、易于实现,但是它忽略了模型参数的先验分布信息。 在最大似然估计中,假设我们有一个模型 f,参数为 θ,观察数据为 x。则似然函数可以定义为 P(x|θ)。为了找到使似然函数最大的参数 θ,我们可以对似然函数取对数,然后对参数 θ 求导数,最后解似然方程。例如,在伯努利分布中,如果我们有 n 个独立同分布的采样值 x1,x2,…,xn,那么似然函数可以表示为: P(x|θ) = ∏[P(xi|θ)] 其中 P(xi|θ) 是每个采样值的伯努利分布概率函数。 在实际应用中,最大似然估计可以用于解决各种问题,例如估计人口的身高分布、估计罐中白球和黑球的比例等。 最大似然估计的缺点是忽略了模型参数的先验分布信息。为了解决这个问题,最大后验估计(Maximum a Posteriori Estimation,MAP)方法被提出。 最大后验估计是贝叶斯估计的一种特定形式,它将模型参数的先验分布信息纳入似然函数中。假设我们有一个模型 f,参数为 θ,观察数据为 x 先验分布为 g(θ)。那么似然函数可以定义为: P(x|θ) \* g(θ) 其中 g(θ) 是参数 θ 的先验分布函数。最大后验估计的目标是找到使似然函数最大的参数 θ。 最大后验估计的优点是可以考虑模型参数的先验分布信息,从而提高估计的准确性。例如,在估计罐中白球和黑球的比例时,最大后验估计可以考虑模型参数的先验分布信息,从而提高估计的准确性。 最大似然估计和最大后验估计都是统计学方法,用于估计模型参数。最大似然估计简单、易于实现,但是忽略了模型参数的先验分布信息。最大后验估计可以考虑模型参数的先验分布信息,从而提高估计的准确性。
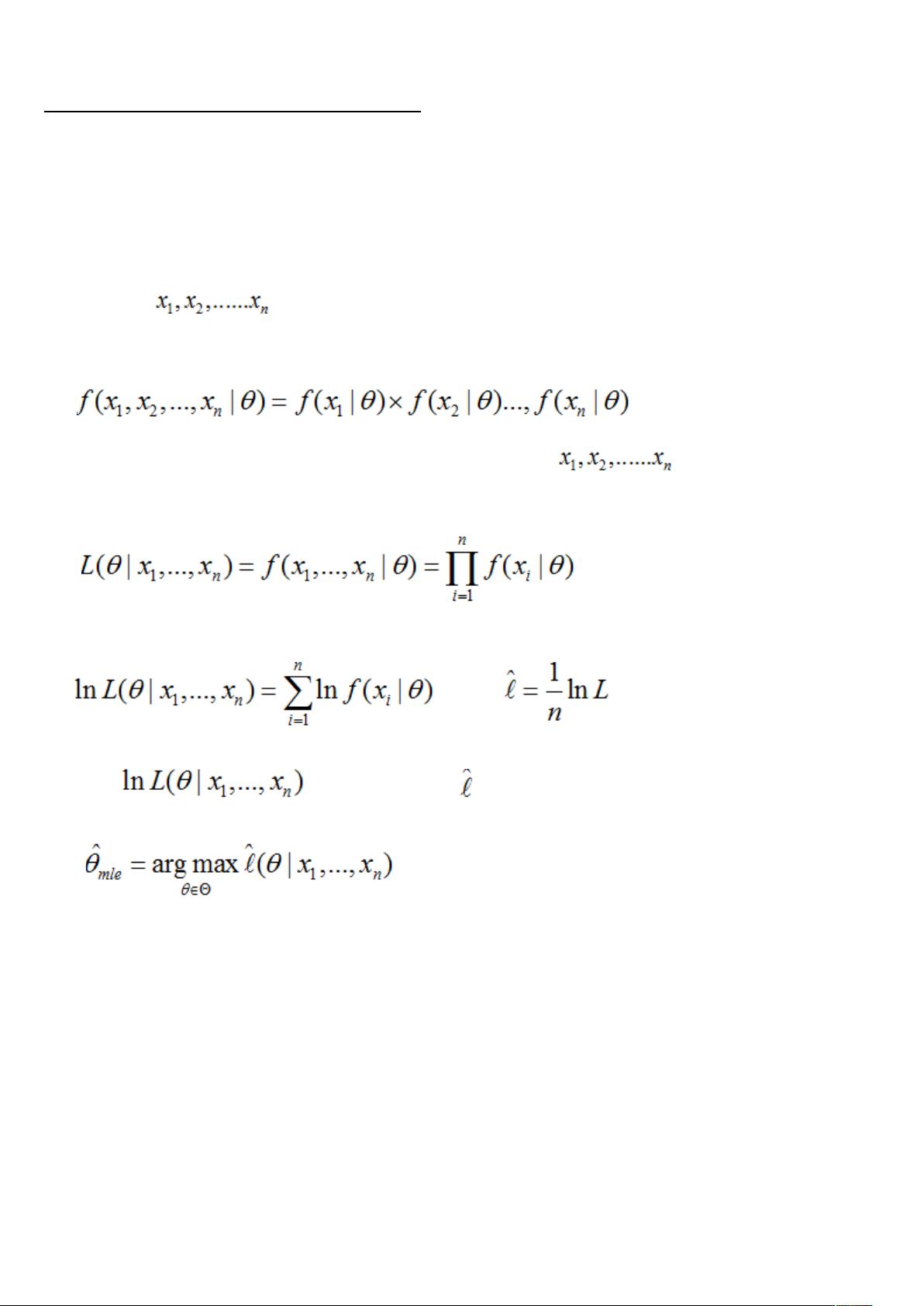

- 粉丝: 5
- 资源: 17
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功