算法设计与分析期末复习（知识点+习题详解）

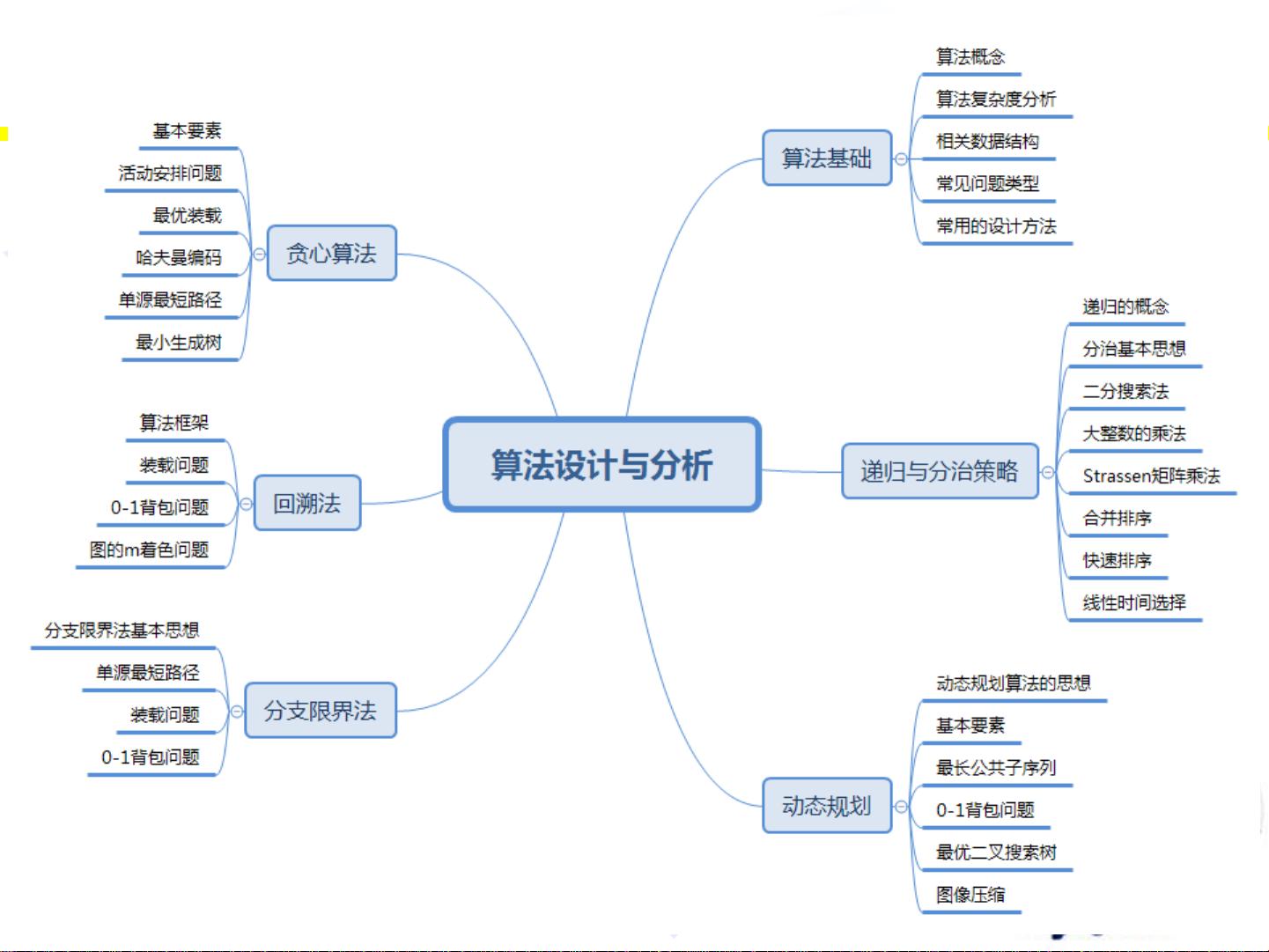
算法设计与分析期末复习的主要章节如下： 第1章算法引论 第2章递归与分治法 第3章动态规划 第4章贪心方法 第5章回溯法 第6章分支限界法 文档中包括各个重要章节的重难点知识还有部分常考习题解析，其中分求解0-1背包问题（分支限界法）单源最短路径问题、装载问题（回溯法）等等都做了很好的标注。 ### 算法设计与分析期末复习知识点及习题详解 #### 第1章 算法引论 **1.1 算法与程序** - **算法的定义**: 算法是一种精确且完整的解题方案描述，它是解决问题的具体方法和步骤。 - **算法的特征**: - **输入**(Input): 可能没有输入，也可能有多个输入。 - **输出**(Output): 至少有一个输出结果。 - **确定性**(Definiteness): 每一步骤必须明确无误。 - **可行性**(Effectiveness): 所有操作都是基本且可执行的。 - **有穷性**(Finiteness): 必须在有限步骤内完成。 **1.2 复杂性分析** - **时间复杂度**: - **渐进时间复杂度**: 用于衡量算法运行时间随问题规模增长的趋势。 - **渐进表示法**: - **O(大O)**: 上界表示法，表示最坏情况下算法运行时间的增长率。 - **Ω(大Omega)**: 下界表示法，表示最好情况下算法运行时间的增长率。 - **Θ(大Theta)**: 精确界表示法，表示算法平均情况下的运行时间增长率。 **1.3 时间复杂度分类** - **多项式时间算法**(Polynomial Time Algorithm): 渐近时间复杂度为多项式级别的算法。 - **指数时间算法**(Exponential Time Algorithm): 渐近时间复杂度为指数级别的算法。 - **常见的时间复杂度排序**: - O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < ... < O(2^n) < O(n!) < O(n^n) #### 第2章 递归与分治法 **2.1 递归的基本概念** - **递归定义**: 一种通过调用自身来解决问题的方法。 - **递归的基本要素**: - 基本情况(Base Case): 最简单的情况，可以直接求解。 - 递归步骤(Recursive Step): 将问题分解成更小的问题，并通过调用自身来解决这些子问题。 **2.2 分治法** - **分治法原则**: - 将问题分解成若干个子问题。 - 解决子问题。 - 合并子问题的解得到最终解。 - **经典应用案例**: - 归并排序(Merge Sort) - 快速排序(Quick Sort) #### 第3章 动态规划 **3.1 动态规划原理** - **定义**: 一种将问题分解成互相重叠的子问题来求解的方法。 - **关键特性**: - 子问题重叠(Subproblem Overlap): 不同子问题之间存在重叠。 - 最优子结构(Optimal Substructure): 问题的最优解包含子问题的最优解。 - **动态规划步骤**: - 定义状态(State Definition) - 状态转移(State Transition) - 边界条件(Boundary Conditions) **3.2 经典案例** - **0-1背包问题**: 使用动态规划方法解决背包容量限制下的物品选择问题。 - 状态定义: dp[i][j] 表示前 i 件物品放入容量为 j 的背包所能获得的最大价值。 - 状态转移方程: dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]) 其中 w[i] 和 v[i] 分别是第 i 件物品的重量和价值。 #### 第4章 贪心方法 **4.1 贪心策略** - **贪心算法定义**: 在每一步都做出局部最优选择，希望这样能够达到全局最优。 - **贪心算法的适用条件**: - 无后效性(No Aftereffect): 选择一旦做出，就不会再改变。 - 贪心选择性质(Greedy Choice Property): 局部最优解组合起来构成全局最优解。 - **应用场景**: - 单源最短路径问题(Dijkstra算法) **4.2 Dijkstra算法详解** - **算法思想**: - 初始化距离表。 - 从未确定最短路径的顶点中选取具有最短临时路径的顶点。 - 更新该顶点所有邻接顶点的距离。 - 重复直到所有顶点的最短路径都被确定。 #### 第5章 回溯法 **5.1 回溯法原理** - **回溯法定义**: 通过试探搜索来寻找问题的所有(或某个)解的算法。 - **核心思想**: - 递归地尝试所有可能的解。 - 当发现当前路径无法达到解时，回退到最近的一个选择点。 - **应用场景**: - 装载问题: 一种经典的组合优化问题，目标是在满足一定约束条件下最大化装载量。 **5.2 装载问题详解** - **问题描述**: 给定一组物品和一个装载容器，每个物品有自己的体积和价值，目标是在不超过容器容积的前提下最大化装载的价值。 - **回溯法求解**: - 定义状态空间树。 - 采用深度优先搜索遍历状态空间树。 - 使用剪枝技术避免无效搜索路径。 #### 第6章 分支限界法 **6.1 分支限界法概述** - **分支限界法定义**: 一种通过广度优先或最小成本优先的方式搜索解空间树的方法。 - **特点**: - 每次扩展一个最接近解的节点。 - 适用于求解最优解问题。 - **应用场景**: - 0-1背包问题: 与回溯法相比，分支限界法更关注于找到最优解。 **6.2 0-1背包问题详解** - **问题描述**: 给定一组物品和一个背包，每个物品有自己的重量和价值，目标是在不超过背包容量的前提下最大化装载的价值。 - **分支限界法求解**: - 定义状态空间树。 - 采用广度优先或最小成本优先的策略遍历状态空间树。 - 使用剪枝技术避免无效搜索路径。 以上内容涵盖了算法设计与分析课程的主要知识点，包括算法的基本概念、复杂度分析、递归与分治法、动态规划、贪心方法、回溯法以及分支限界法。通过对这些知识点的学习，可以帮助学生深入理解算法设计的基本原理及其应用，并能够在实际问题中灵活运用这些算法。