SVM的原理介绍
### 支持向量机(SVM)的基本原理与应用 #### 一、引言 支持向量机(Support Vector Machine, SVM)是一种强大的监督学习算法,主要用于分类和回归问题。自1995年Vladimir Vapnik及其团队在AT&T贝尔实验室首次提出以来,SVM因其卓越的泛化能力而在机器学习领域获得了广泛的关注和应用。本文将基于给定的文章内容深入探讨SVM的基本原理、特点以及其实现方式。 #### 二、SVM的基本概念 SVM的核心思想是寻找一个最优的决策边界(称为超平面),该边界能够最大化地分隔两类数据点,并确保最大的间隔(margin)。这种最大间隔原则有助于提高模型的泛化能力,即模型能够在未见过的数据上表现良好。 ##### 1. 分类问题 假设我们有两个类别C1和C2的数据集,我们需要找到一个超平面,使得C1和C2之间的距离尽可能大。这个距离被称为“间隔”,它是支持向量到超平面的最短距离的两倍。 ##### 2. 非线性可分问题 在现实世界的应用中,很多情况下数据并非线性可分。为了解决这个问题,SVM引入了核技巧(Kernel Trick),通过将原始数据映射到高维空间来实现非线性分类。这种映射可以是多项式核函数、径向基函数(RBF)等。 #### 三、SVM的工作原理 ##### 1. 线性可分情况 当训练数据完全线性可分时,可以通过求解一个凸优化问题来找到最优超平面。具体来说,SVM试图最小化以下目标函数: \[ \min_{\mathbf{w}, b} \frac{1}{2}\|\mathbf{w}\|^2 + C \sum_{i=1}^{n} \xi_i \] 其中,\(\mathbf{w}\)表示权重向量,\(b\)表示偏置项,\(\xi_i\)是松弛变量,用来处理不完全线性可分的情况,而\(C\)是一个正则化参数,用于平衡分类间隔和错误分类之间的关系。 ##### 2. 非线性可分情况 对于非线性可分的数据,SVM利用核技巧将低维空间中的非线性关系转换为高维空间中的线性关系。常用的核函数包括: - **线性核**:\(K(x, y) = x \cdot y\) - **多项式核**:\(K(x, y) = (x \cdot y + c)^d\) - **径向基函数核**:\(K(x, y) = \exp(-\gamma \|x - y\|^2)\) 这些核函数的选择对SVM的性能有着重要的影响。 #### 四、SVM的特点 - **鲁棒性**:即使在少量样本的情况下,SVM也能保持较好的性能。 - **泛化能力强**:由于最大间隔原则,SVM具有较强的泛化能力。 - **对高维特征空间的适应性**:核技巧使得SVM能够处理高维数据。 - **稀疏性**:最终模型只依赖于支持向量,这大大减少了计算成本。 #### 五、SVM的应用案例 文章提到的一个实际应用案例是光学字符识别(OCR)。SVM被证明在这种场景下比传统学习算法具有更好的性能。通过使用多项式输入变换的SVM网络,实验结果显示其具有较高的泛化能力。 #### 六、结论 支持向量机是一种功能强大且实用的机器学习算法,它不仅适用于线性分类问题,还能够通过核技巧解决非线性分类问题。SVM的理论基础及其在实际应用中的优异表现使其成为许多领域的首选工具之一。对于希望深入了解并应用这一技术的研究者和实践者而言,掌握SVM的基本原理和操作技巧至关重要。


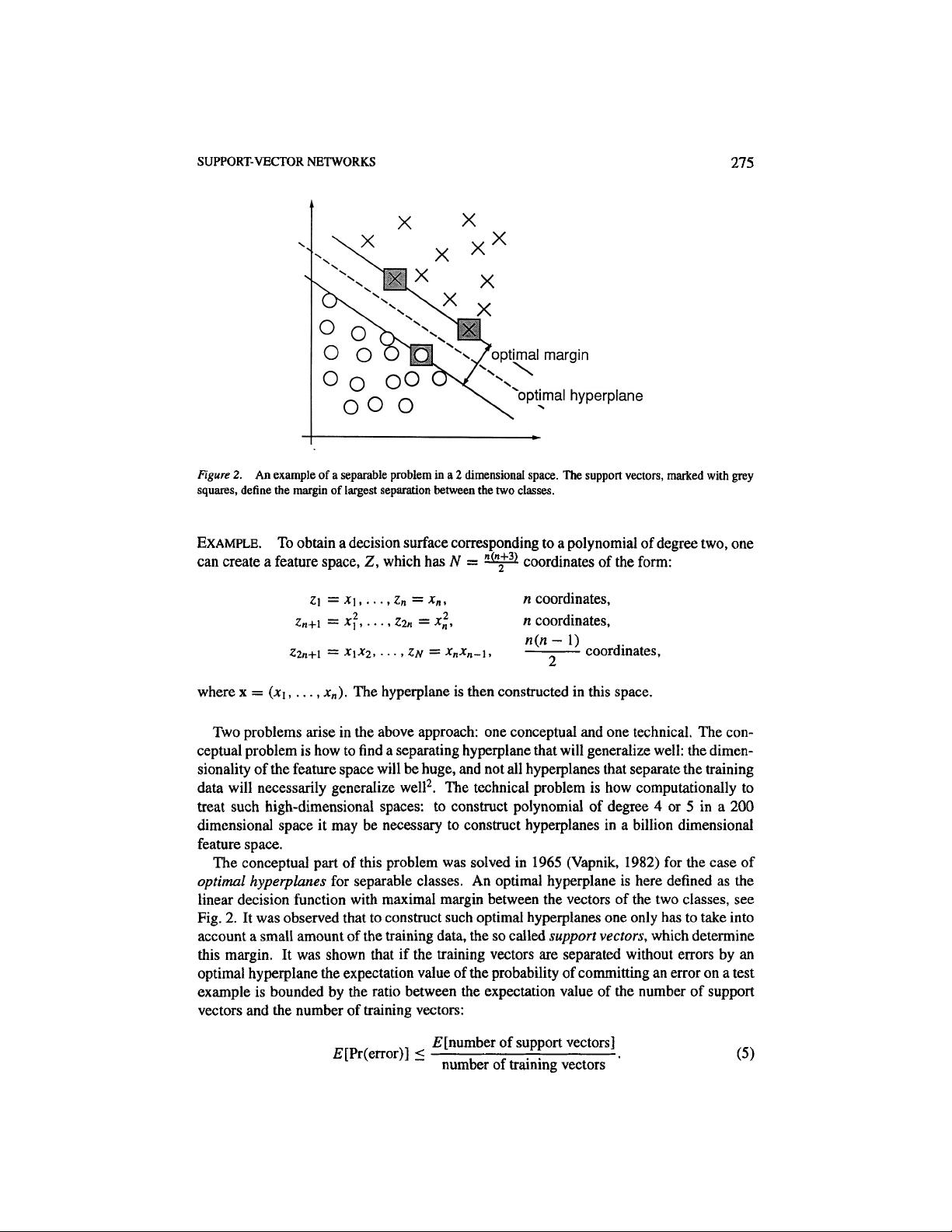

剩余24页未读,继续阅读

 ElricYM2012-12-28挺好的,不过是英文的
ElricYM2012-12-28挺好的,不过是英文的
- 粉丝: 2
- 资源: 5
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功