220号资源-源程序：基于Newton-Raphson：一种新的基于群体的元启发式算法（附带WORD)-本人博客有解读资源-CSDN文库

共9个文件

m：6个

png：2个

pdf：1个

版权申诉

启发式算法

182 浏览量 2024-10-20 17:15:34 上传评论收藏 26.36MB RAR 举报

资源推荐

资源详情

资源评论

收起资源包目录

NRBO_Newton_Raphson_Based_Optimizer.rar （9个子文件）

NRBO_Newton_Raphson_Based_Optimizer

initialization.m 2KB

SearchRule.m 3KB

2GK9JAYLN$`4T{RN6N02FWG.png 270KB

Get_Functions_details.m 8KB

Newton-Raphson-based optimizer A new population-based metaheuristic algorithm for continuous optimization probles.pdf 32.83MB

Main.m 2KB

func_plot.m 4KB

NRBO.m 6KB

~D4CNTIVIVU9I%}K}{M(SQ2.png 173KB

Engineering Applications of Articial Intelligence 128 (2024) 107532

Available online 12 December 2023

Newton-Raphson-based optimizer: A new population-based metaheuristic

algorithm for continuous optimization problems

Ravichandran Sowmya

, Manoharan Premkumar

, Pradeep Jangir

Department of Electrical and Electronics Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, Karnataka 576104, India

Department of Electrical and Electronics Engineering, Dayananda Sagar College of Engineering, Bengaluru, Karnataka, 560078, India

Rajasthan Rajya Vidyut Prasaran Nigam, Sikar, 332025, Rajasthan, India

ARTICLE INFO

Keywords:

Constrained problems

Internet of vehicle

Metaheuristics

Newton-Raphson-based optimizer

Newton-Raphson search rule

Trap avoidance operator

ABSTRACT

The Newton-Raphson-Based Optimizer (NRBO), a new metaheuristic algorithm, is suggested and developed in

this paper. The NRBO is inspired by Newton-Raphson’s approach, and it explores the entire search process using

two rules: the Newton-Raphson Search Rule (NRSR) and the Trap Avoidance Operator (TAO) and a few groups of

matrices to explore the best results further. The NRSR uses a Newton-Raphson method to improve the explo-

ration ability of NRBO and increase the convergence rate to reach improved search space positions. The TAO

helps the NRBO to avoid the local optima trap. The performance of NRBO was assessed using 64 benchmark

numerical functions, including 23 standard benchmarks, 29 CEC2017 constrained benchmarks, and 12 CEC2022

benchmarks. In addition, the NRBO was employed to optimize 12 CEC2020 real-world constrained engineering

optimization problems. The proposed NRBO was compared to seven state-of-the-art optimization algorithms, and

the ndings showed that the NRBO produced promising results due to its features, such as high exploration and

exploitation balance, high convergence rate, and effective avoidance of local optima capabilities. In addition, the

NRBO also validated on challenging wireless communication problem called the internet of vehicle problem, and

the NRBO was able to nd the optimal path for data transmission. Also, the performance of NRBO in training the

deep reinforcement learning agents is also studied by considering the mountain car problem. The obtained results

also proved the NRBO’s excellent performance in handling challenging real-world engineering problems.

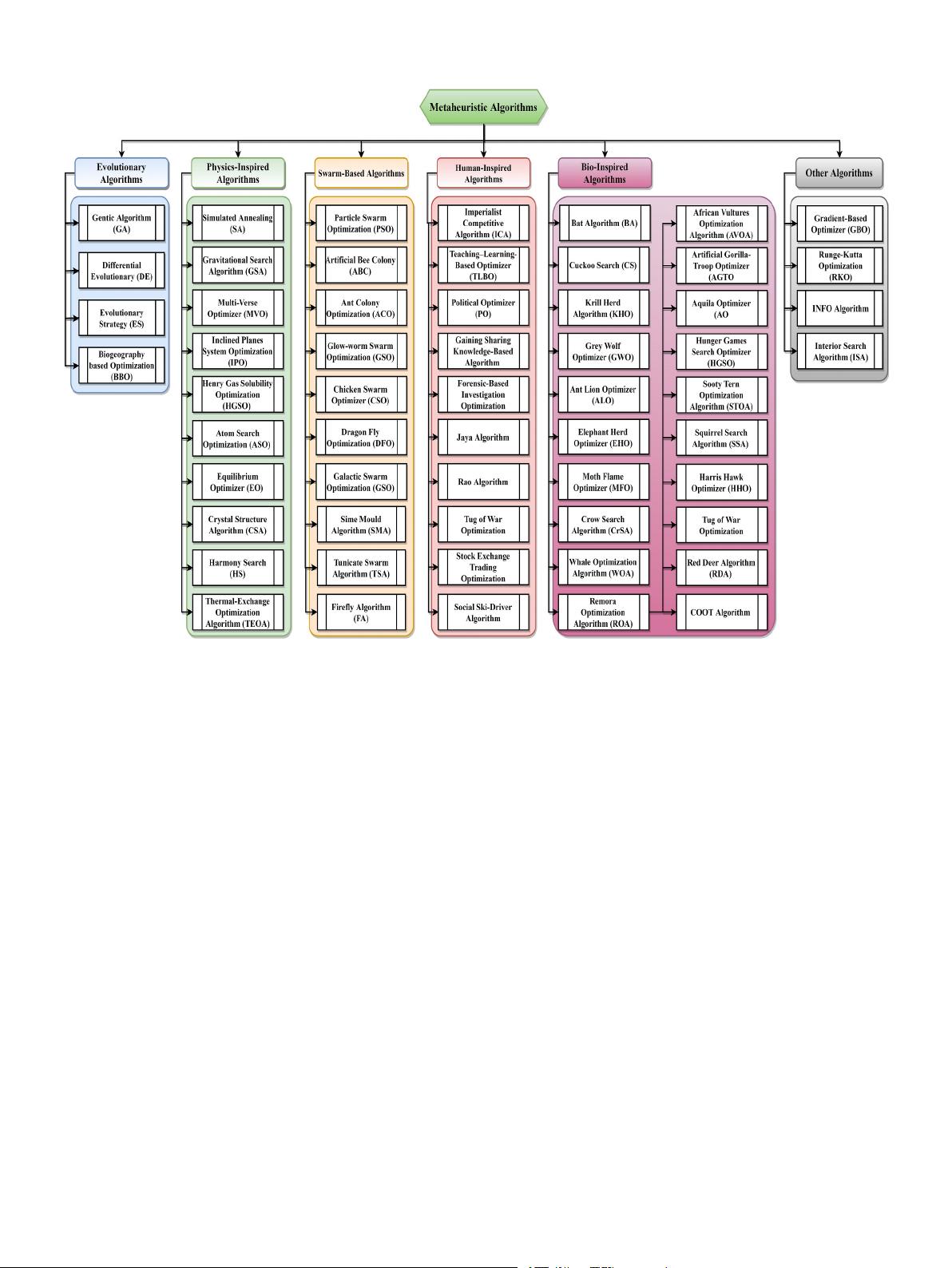
1. Introduction

The past several years have seen a urry of interest in real-world

optimization problems that are difcult to solve in various elds,

together with but not restricted to computer science-associated chal-

lenges and data analytics, as well as wireless communication and engi-

neering design challenges (Abdel-Basset et al., 2018). Common features

of such optimization problems include the presence of constraints, de-

cision variables, objectives, and other similar elements. Today’s modern

research, particularly in engineering and manufacturing control prob-

lems, heavily relies on applying optimization algorithms (Halim et al.,

2020; Sreedhar et al., 2020). Analytical or numerical programming and

heuristics or metaheuristic techniques are two categories used to solve

real-world engineering problems (Osaba et al., 2021). The initial clas-

sication of the Metaheuristic Algorithm (MA) separates it into two

categories: single-solution and population-based algorithms.

Single-Solution-Based (SSB) algorithms are more efcient than

population-based algorithms. Depending on their complexity, numerous

real-world problems could be characterized as single-objective, multi--

objective, or multimodal optimization problems. Because of such

complicated features, conventional mathematical methods such as

gradient descent and conjugate gradient cannot handle these situations

efciently and effectively (Okwu and Tartibu, 2021; Kumar et al., 2022).

On the other hand, the MA of the latter categories is not gradient-

based and, as a result of their randomized behaviour, has a high likeli-

hood of avoiding local optima (Gong et al., 2020; Abualigah et al.,

2021). The MAs provide many advantages over traditional techniques,

including ease of implementation, reliability, and efciency. Because of

such characteristics, MAs can overcome the limitations of classic

methodologies, such as early convergence and local optima stalling

(Dr

eo et al., 2006). When handling optimization problems, because MAs

are members of the randomized optimization class, they gain from using

stochastic operators to prevent locally optimum solutions as much as

possible (Oliva et al., 2021). In MAs, the two important search stages are

exploration and exploitation. These two phases must be balanced to get

* Corresponding author.

E-mail addresses: sowmyanitt@gmail.com (R. Sowmya), mprem.me@gmail.com (M. Premkumar), pkjmtech@gmail.com (P. Jangir).

Contents lists available at ScienceDirect

Engineering Applications of Articial Intelligence

journal homepage: www.elsevier.com/locate/engappai

https://doi.org/10.1016/j.engappai.2023.107532

Received 24 February 2022; Received in revised form 30 August 2023; Accepted 14 November 2023

Engineering Applications of Articial Intelligence 128 (2024) 107532

the best optimal solutions. Consequently, MAs are suitable for various

situations in both research and industrial applications due to their spe-

cic qualities (Costa and Oliveira, 2003). A typical disadvantage of most

MAs, on the other hand, is that they are often resistant to parameter

tuning that the inventor chooses. On the other hand, the MAs may not

necessarily lead to global optimum solutions (Okwu and Tartibu, 2021;

eo et al., 2006). Aside from that, they are typically more computa-

tionally expensive than traditional algorithms because they use a pop-

ulation of solutions. The MAs can be divided into Swarm Intelligence

(SI) and Evolutionary Algorithms (EA) (Hussain et al., 2018). Nature’s

evolutionary principles inspire the EAs. For instance,

Biogeography-Based Optimization (BBO) (Simon, 2008), Differential

Evolution (DE) (Kumar et al., 2022; Qin et al., 2009), Genetic Algo-

rithms (GA) (Goldberg and Holland, 1988), Evolutionary Strategy (ES)

(Rechenberg, 1989), etc., are a few algorithms in the EA category.

However, their parameters must be ideally adjusted before starting the

optimization procedure to prevent the local optima trap. As a result,

numerous studies have been conducted to determine the optimal pa-

rameters for such EAs.

The SI algorithms are a form of articial intelligence used to replicate

the communal characteristics of social swarms in the environment. It is

possible to achieve this by having agents follow local rules without

centralized control. The aggregate capabilities of the swarm are signif-

icantly more extensive than the sum of individual swarm behaviours.

The SI algorithms generate more than one randomized solution and

rene those solutions over the optimization procedure. SI comprises

Particle Swarm Optimization (PSO) (Eberhart and Kennedy, 1995; Shi

and Eberhart, 1998) and Ant Colony Optimization (ACO) (Dorigo et al.,

1996), which are probably the most common methods. For instance, the

ACO simulates ants’ social actions to identify the shortest distance be-

tween the food source and the nest. The PSO mimics the movement of a

ock of birds and their foraging activity. Recently, numerous SI algo-

rithms have been reported for solving various optimization problems.

For instance, Articial Bee Colony (ABC) (Karaboga and Basturk, 2007),

Bat Algorithm (BA) (Bora et al., 2012), Cuckoo Search (CS) (Yang and

Deb, 2010), Glow-worm swarm optimization (Li and Huang, 2016),

Grey Wolf Optimizer (GWO) (Mirjalili et al., 2014; Premkumar et al.,

2022), Dragon Fly Optimizer (DFO) (Khishe and Safari, 2019), Firey

algorithm (Johari et al., 2013), Ant Lion Optimizer (ALO) (Mirjalili,

2015a), Moth Flame Optimizer (MFO) (Mirjalili, 2015b), Emperor

Penguin Optimizer (EPO) (Dhiman and Kumar, 2018), Elephant Herding

Optimizer (EHO) (Jadoun et al., 2021), buttery optimization (Arora

and Singh, 2019), Salp Swarm Algorithm (SaSA) (Mirjalili et al., 2017),

Whale Optimization Algorithm (WOA) (Mirjalili and Lewis, 2016),

chicken swarm optimizer (Meng et al., 2014), Crow Search Algorithm

(CrSA) (Zamani et al., 2019), elephant clan optimizer (Jafari et al.,

2021), Mante-Ray Foraging Optimizer (MRFO) (Zhao et al., 2020), Red

Deer Algorithm (RDA) (Fathollahi-Fard et al., 2020), Harris Hawks

Optimizer (HHO) (Heidari et al., 2019), Spotted Hyena Optimizer (SHO)

(Dhiman and Kumar, 2017), Slime Mould Optimizer (SMO) (Li et al.,

2020), Squirrel Search Algorithm (SSA) (Jain et al., 2019), Marine

Predator Algorithm (MPA) (Faramarzi et al., 2020a), tunicate swarm

algorithm (Kaur et al., 2020), Hunger Games Search Optimizer (HGSO)

(Manjula Devi et al., 2022), Sooty Tern Optimization Algorithm (STOA)

(Dhiman and Kaur, 2019), Aquila Optimizer (AO) (Abualigah et al.,

2021), Articial Gorilla-Troop Optimizer (AGTO) (Abdollahzadeh et al.,

2021a), African Vultures Optimization Algorithm (AVOA) (Abdollah-

zadeh et al., 2021b), COOT Algorithm (Naruei and Keynia, 2021),

Remora Optimization Algorithm (ROA) (Jia et al., 2021), etc. are a few

algorithms in SI category. The following are mostly preferred

Population-Based (PB) optimization algorithms: Simulated Annealing

(SA) (Kirkpatrick et al., 1983), harmony search (Geem et al., 2001),

imperialist competitive algorithm (Shahrazad and Alikhanzadeh, 2015),

gravitational search algorithm (Rashedi et al., 2009), Teach-

ing–Learning-Based Optimizer (TLBO) (Crawford et al., 2020), Krill

Herd (Gandomi and Alavi, 2012), Interior Search Algorithm (ISA)

(Trivedi et al., 2016), Multi-Verse Optimizer (MVO) (Mirjalili et al.,

2016), Inclined Planes system Optimization (IPO) (Mozaffari et al.,

2016), Henry Gas Solubility Optimization (HGSO) (Hashim et al., 2019),

Atom Search Optimization (ASO) (Irudayaraj et al., 2022), Political

Optimizer (PO) (Askari et al., 2020), Equilibrium Optimizer (EO) (Far-

amarzi et al., 2020b), Gradient-Based Optimizer (GBO) (Ahmadianfar

et al., 2020; Premkumar et al., 2021a), Runge-Kutta Optimization (RKO)

(Ahmadianfar et al., 2021), Crystal Structure Algorithm (CSA) (Talata-

hari et al., 2021), etc. Further, the algorithms are classied as EAs,

swarm-based, physics-inspired, human-inspired, and bio-inspired. Fig. 1

illustrates the broad classication of metaheuristic algorithms.

As seen in Fig. 1, most MAs created are based on population infor-

mation. Algorithms preserve and enhance several candidate solutions by

using various operators. On the other hand, an SSB applies a solution to

discover the optimal solution. When a population of solutions is utilized

to search for good solutions in a region, the likelihood of nding viable

solutions among the candidate solutions is greater than one. However,

compared to SSB algorithms, PB strategies often need more time, and, in

addition, the majority do not have a decent or greedy intensication

phase. Nevertheless, it is clear that the number of SSB approaches is far

lower than the PB algorithms (Fathollahi-Fard et al., 2018).

Studies have extensively concentrated on PB algorithms during the

Nomenclature

- Initial or starting point

n+1

- Next approximation

′

(x), f

″

), f

‴

) - First-order, second-order, and third-order

derivatives

lb and ub - Lower and upper bounds

dim - Problem dimension

- Decision vector/variable

- Population size

- Population matrix

and X

- Best and worst population position, respectively

δ - Adaptive coefcient for balancing exploration and

exploitation

IT - Current iteration

Max

IT - Maximum number of iterations

- Adaptive coefcient for improving exploitation

and r

- Random integers

, a and b - Uniform random numbers between (0,1)

and θ

- Uniform random numbers between (− 1,1) and

(− 0.5,0.5)

β - Binary number, either 1 or 0

- Current vector position

and X

- Random position vectors

- New vector position by updating x

- New vector position by considering X

, X

and X

New vector position by considering X1

, X2

, and x

div

- Average population diversity

div

max

- Maximum population diversity

- Probability of route link

- Probability of packet reception

D - Route delay

) - Threshold value for the delay

T - Time variation of the graphical model

G(i, s) - Network map

R. Sowmya et al.

Engineering Applications of Articial Intelligence 128 (2024) 107532

last three decades, with only a few SSB algorithms. The SSB algorithms

are less complicated than PB algorithms. Generally, the PB methods can

be categorized into gradient-based (GB) methods and MAs. The

gradient-based methods have been broadly employed to solve optimi-

zation problems. An extreme point at which the gradient is equal to zero

must be identied to determine an optimal solution using the gradient-

based methods. Exploring the search directions in these methods re-

quires determining the derivatives of the objective function and the

constraints. The two main disadvantages of this type of optimization are:

(1) the convergence speed is very slow, and (2) there is no guarantee of

achieving the optimal solution. Some initial points (i.e., population) are

randomly generated in the second category. Each point has a search

direction determined by the information acquired from previous results.

The optimization process is continued by updating the search directions

until the convergence criterion is met. Such optimization techniques (i.

e., MAs) have been widely utilized to optimize engineering problems.

The MAs provide great robustness to nding the global optima, while

the gradient-based methods tend to converge into local optima. How-

ever, the non-gradient-based methods require higher computational

capacities, especially for problems with high-dimensional search spaces.

Hence, it will be very worthwhile to develop an optimization method

that uses a gradient method to skip the unfeasible points and move to-

wards the feasible area and also takes advantage of the capabilities of the

population-based optimization methods.

Despite the variety in such algorithms, there seems to be one thing

they all have in prevalent: MAs split the search procedure into two

stages: exploitation and exploration. The exploratory phase occurs when

an MA seeks to locate the best regions of a particular search space using

a variety of search parameters. An MA should utilize its random oper-

ators to comprehensively investigate diverse portions of the search

region. On the other hand, the exploitation stage enables the optimi-

zation to focus on the neighbourhood of the entire search space that

contains higher-quality solutions rather than the entire search area

(Premkumar et al., 2021b). The contradictory nature of exploitation and

exploration necessitates using a robust and reliable optimizer to balance

the exploitative and exploratory abilities. The local optima trap signif-

icantly increases if the balance between exploration and exploitation is

not properly balanced (Li et al., 2021).

In addition to the MAs, Reinforcement Learning (RL) is also getting

more attention to solve optimization problems. The RL is a machine

learning paradigm where an agent learns to make decisions by inter-

acting with an environment. The agent takes action in the environment

and receives rewards based on the results, aiming to maximize the cu-

mulative reward over time (Mazyavkina et al., 2021). Deep Reinforce-

ment Learning (DRL) combines RL with Deep Learning (DL) techniques,

using neural networks to approximate the policies or value functions.

DRL can be applied to optimization problems where the

decision-making process can be modelled as a sequence of decisions or

actions (Dell’Aversana and Dell’Aversana, 2022; Dussauge et al., 2023).

For instance, Deep Q-Networks (DQN) combines Q-learning with deep

neural networks. It was one of the pioneering methods that showed the

potential of combining RL with DL, initially used to play Atari games but

later extended to optimization problems (Mnih et al., 2015). Some other

applications are as follows: (i) Deep Deterministic Policy Gradients

(DDPG) algorithm that adapts the concepts of DQN for continuous ac-

tion spaces. It is valuable for optimization problems where actions are

not discrete (Silver et al., 2014); (ii) Proximal Policy Optimization (PPO)

tries to balance exploiting known good actions and exploring new ones.

It is known for its stability in training, which can be crucial for many

optimization tasks (Schulman et al., 2017); (iii) Actor-critic (AC)

Fig. 1. Broad classication of metaheuristic algorithms.

R. Sowmya et al.

Engineering Applications of Articial Intelligence 128 (2024) 107532

methods combine the benets of value-based and policy-based methods.

An actor learns the policy, and a critic evaluates it (Mnih et al., 2016;

Haarnoja et al., 2018). This combination can speed up the learning

process for optimization problems. Silver et al. (2014) demonstrated

using DRL for continuous control tasks with DDPG (Silver et al., 2014).

Bello et al. (2016) used DRL to tackle the travelling salesman problem,

showing that DRL methods could produce near-optimal solutions and

sometimes outperform traditional heuristics (Bello et al., 2016). The

authors of (S

anchez et al., 2022) have reviewed DRL for efcient

resource allocation in computer systems. Lillicrap et al. (2015) imple-

mented DDPG for various robotic control tasks, pushing the boundaries

of what DRL could achieve in real-world settings (Lillicrap et al., 2015a).

Schulman et al. (2017) introduced PPO, enhancing training stability,

which is particularly crucial for challenging optimization tasks (Schul-

man et al., 2017). Andrychowicz et al. (2017) developed hindsight

experience replay to help agents learn from failures, proving useful for

certain optimization scenarios where failure experiences are abundant

(Andrychowicz et al., 2017).

DRL algorithms often require a signicant amount of data to achieve

good performance. Balancing exploration and exploitation remains a

challenge. Novel techniques like entropy regularization have been pro-

posed to address this (Haarnoja et al., 2018). Training DRL agents for

one optimization problem does not guarantee performance on another.

Work on meta-learning and transfer learning, like that by (Finn et al.,

2017), provides a promising avenue. The authors of (Grumbach et al.,

2022a, 2022b) have compared the performance of DRL methods against

traditional metaheuristic algorithms, nding mixed results dependent

on problem specics. Researchers have proposed hybrid models, inte-

grating DRL with metaheuristics, to benet from the strengths of both

methods (Kosanoglu et al., 2022; Chen et al., 2020). While DRL has

shown promise for various optimization problems, the eld is still

evolving. Challenges remain, especially regarding training stability,

sample efciency, and transferability. Future research may delve deeper

into hybrid models, adaptive exploration techniques, and improved

sample efciency. Though the DRL methods are advantageous over the

metaheuristic algorithms in solving some complex optimization prob-

lems, it has several drawbacks. (i) Training deep neural networks can be

time-consuming and computationally expensive; (ii) DRL algorithms can

sometimes be unstable during training, particularly if not correctly

tuned; (iii) DRL usually requires a signicant amount of data or in-

teractions with the environment; however, the metaheuristic algorithms

do not necessarily have this demand; (iv) Metaheuristic algorithms often

have intuitive steps and can be easier to interpret than DRL models; (v)

DRL models can overt to their training environments, leading to poor

performance on new, unseen instances of the optimization problem; (vi)

Setting up and tuning DRL models usually demands a deeper under-

standing of both RL and DL, which might not be the case for some

metaheuristic algorithms.

Deep reinforcement learning has shown signicant potential in

solving optimization problems, offering the ability to generalize across

problem instances and handle large-scale and complex problems.

However, its adoption comes with challenges, including long training

times and potential stability issues. Traditional metaheuristic algorithms

still nd relevance due to their simplicity, transparency, and suitability

for specic problems. The choice between DRL and metaheuristics de-

pends on the optimization problem, available computational resources,

and the practitioner’s expertise.

On the other hand, even though most PB algorithms are preferred for

optimization problems and effectively balance the exploration and

exploitation stages, algorithms require several stages and numerous

parameters to be tuned. Furthermore, according to the No-Free-Lunch

(NFL) theory, none of the previously listed metaheuristics can solve all

optimization problems (Wolpert and Macready, 1997). According to this

theorem, a new algorithm that outperforms present metaheuristics on

current or future problems is always possible as long as it is based on

current or future optimization problems. The metaheuristic algorithms

can not always promise to nd the global optima for every optimization

problem because of the random elements in the search mechanisms. A

difcult and unsolved challenge with metaheuristic algorithms is

nding a good balance between exploration and exploitation. Addi-

tionally, according to the NFL theory, no single optimization technique

can handle all possible optimization problems. NFL also suggests that

this eld of research is quite dynamic, encouraging the years-long in-

vention of numerous new metaheuristic optimization techniques. This

work proposes a new metaheuristic algorithm with population-based

features named “Newton-Raphson-Based Optimizer (NRBO)” to close

the research gap.

The metaheuristic algorithms provide great robustness to nd the

global optima, while the gradient-based methods tend to converge into

local optima. However, the non-gradient-based methods require higher

computational capacities, especially for problems with high-

dimensional search spaces. Hence, it will be very worthwhile to

develop an optimization method that uses a gradient method to skip the

unfeasible points and move towards the feasible area and also takes

advantage of the capabilities of the population-based optimization

methods. Thus, one of the unique features of this study is to combine the

concept of the gradient-based method with the population-based

method to create a powerful and efcient NRBO algorithm to over-

come the drawbacks of gradient and non-gradient algorithms. As a

result, the above-said limitations motivate our attempt to build a novel

population-based metaheuristic algorithm called NRBO that is simple

and efcient. The proposed NRBO is inspired by Newton-Raphson’s

approach, and it explores the entire search process using two rules: the

Newton-Raphson Search Rule (NRSR) and the Trap Avoidance Operator

(TAO) and a few groups of matrices to explore the best results further.

The main contributions of the paper are listed as follows.

• A new population-based metaheuristic algorithm called NRBO

inspired by the Newton-Raphson method is proposed and analyzed.

• Two operators called NRSR and TAO are proposed to improve the

exploration and exploitation of NRBO.

• The performance of NRBO is validated using 23 classical benchmark

functions, 29 CEC2017 benchmark functions, and 12 CEC2020 real-

world engineering problems. In addition, 12 CEC2022 benchmarks

are utilized and compared with CEC2022 winners.

• The performance comparison is made among seven newly reported

algorithms using statistical data analysis, convergence analysis,

runtime analysis, balance analysis, and Friedman’s rank statistical

test.

• The capability of NRBO is further investigated on one of the chal-

lenging wireless communication problems called the Internet of

Vehicles (IoV) problem to enhance the data broadcasting over a

reliable path.

• The performance of NRBO in training the DRL agents is also briey

studied by considering the mountain car problem.

The paper is structured as follows: Section 2 discusses the back-

ground study of the MAs and the basic concepts of the Newton-Raphson

method. In addition, the inspiration and mathematical modelling of the

proposed NRBO are comprehensively discussed, along with the formu-

lation procedure of NRSR and TAO. Section 3 discusses the results ob-

tained on classical benchmark problems, CEC2017, and CEC2022

problems and the performance comparison based on several metrics. In

addition, the performance comparison between NRBO and the CEC2022

winners is also discussed. Section 4 presents the results obtained by the

NRBO and other state-of-the-art algorithms on 12 CEC2020 real-world

engineering problems. Section 5 comprehensively discusses the results

of the NRBO and other algorithms on the IoV problem. Section 6 dis-

cusses the performance study of the DRL agents training in mountain car

problems and the summary of the proposed work, limitations, and

challenges, and Section 7 concludes the paper.

R. Sowmya et al.

Engineering Applications of Articial Intelligence 128 (2024) 107532

2. Background and methodology

This section comprehensively discusses the theoretical background

and the concepts of Newton’s method. In addition, the inspiration and

the formulation procedures of the proposed population-based meta-

heuristic algorithm called Newton-Raphson-Based Optimizer (NRBO)

are explained comprehensively.

2.1. Background

Mostly, the optimization algorithms are classied into two cate-

gories: Gradient-Based (GB) algorithms, such as Newton’s Method (NM)

(Amrein and Wihler, 2014), Gradient-Descent Algorithm (GDA)

(Madgwick et al., 2011), Levenberg Marquardt Algorithm (LMA) (Mor

1978), and Quasi-Newton’s Method (QNM) (Weerakoon and Fernando,

2000), and non-gradient-based algorithms called MAs, such as GA, DE,

PSO, ABC, ACO, SA, JAYA algorithm, GWO, SSA, EO, MPA, GBO, RKO,

HGSO, SMO, AGTO, etc., as discussed in earlier. The GB approaches

have been widely used in solving optimization problems in different

applications. Identifying an absolute extreme, where the gradient is

equivalent to 0, is required to discover an optimum solution employing

GB techniques. The NM and conjugate direction methods are GB

methods based on this principle. The GB methods and most other opti-

mization approaches require selecting a search path, after which the

search proceeds in that direction in pursuit of the best solution. In order

to investigate the search directions, it is necessary rst to establish the

derivative of the tness function and the constraints. The two most

signicant drawbacks of GB methods are slow convergence speed and no

assurance that the best solution will be obtained.

In MAs, the selected algorithm produces certain initial population

positions randomly. With respect to each position, a search path is

established by the intelligence gathered from earlier ndings. The

optimization is carried out until the maximum number of iterations or

other convergence conditions by updating the search patterns. The

application of MAs to various real-world engineering problems has

become extremely prevalent. The MAs offer excellent robustness in

searching for optimal solutions, whereas the GB approaches get trapped

by local optimal solutions. On the other hand, the MAs necessitate more

CPU core utilization, which is particularly important for problems with

large search spaces. To avoid impracticable locations and advance to-

wards the viable region, it would be extremely benecial to build an

algorithm that employs a GB and takes advantage of the availability of

population-based algorithms. As a result, one of the unique aspects of

this research is combining Newton’s method with population-based

methods to develop an advanced and effective algorithm that over-

comes the shortcomings of traditional algorithms.

2.2. Newton-Raphson Method (NRM)

Newton’s method, commonly known as the Newton-Raphson

Method (NRM), is a root-nding procedure that uses the rst few com-

ponents of the Taylor Series (TS) of a function f(x) in the region of a

presumed root to locate the root of the function (Chapter 5 Newton,

2007; Bazaraa et al., 2006; Kalantari, 2000). For f(x) a polynomial, NRM

is fundamentally similar to Horner’s method (He and J-S Shiue). The

NRM initiates with a single point (x

) and then employs the TS evaluated

at x

for identifying one more point nearby the previous solution. This

step is repeated until the appropriate solution has been found. The TS of

f(x) about the point (x = x

+ ϵ) is represented as follows.

f (x

+ϵ)=f (x

)+f

′

)ϵ +

″

)(ϵ)

‴

)(ϵ)

+ ⋯ (1)

Keeping the second-order terms,

f (x

+ϵ)≈f

′

)ϵ +

″

)(ϵ)

(2)

Equation (2) can be utilized to nd the offset ϵ required to locate

closer to the root originating from x

. Assume f(x

+ϵ)= 0 and Eq. (2)

solved for ϵ ≡ ϵ

gives,

= −

′

)

″

)

(3)

Eq. (3) is the second-order tuning to the position of the root. By

allowing x

= x

+ ϵ

, determine the next position of the root, and the

procedure can be repeated until it converges to the optimal root using

Eq. (4).

= −

′

)

″

)

(4)

Regrettably, this process can be unbalanced near a local peak or a

horizontal asymptote. Still, the method can be applied iteratively to nd

the next approximation with a proper initial position.

n+1

= x

−

’

)

’’

)

, n = 1, 2, 3, … (5)

In NRM, an approximate zero is a starting point x

that ensures safe

convergence of the algorithm.

2.3. Newton-raphson-based optimizer (NRBO)

The proposed NRBO denes the search path by applying the NRM to

discover the search region using a few vector sets and two operators,

such as NRSR and TAO to explore the search domain.

2.3.1. Initialization

Imagine the following scenario: The optimization is performed on an

unconstrained single-objective optimization problem with the following

denition.

Minimize : f (x

, x

, …, x

)

lb ≤ x

≤ ub, j = 1, 2, …, dim

(6)

where f(x) is the tness function to be minimized, x

denotes the deci-

sion vector, dim represents the problem dimension, lb denotes the lower

bounds, and u b denotes the upper bounds. Like other MH algorithms,

NRBO initiates its search for optimal solutions by producing initial

random populations inside the boundaries of the candidate solutions.

Based on the fact that there are N

number of populations, and each

population consists of dim decision variables/vectors. Therefore, the

random population is generated using Eq. (7).

= lb +rand × (ub − lb), n = 1, 2, …, N

and j = 1, 2, …, dim (7)

where x

denotes the position of j

dimension of n

population, and

rand denotes the random number between (0,1). Eq. (8) presents the

population matrix that can portray the populations with all dimensions.







⋯ x

dim

⋯ x

dim

⋮ ⋮ ⋱ ⋮

⋯ x

dim







×dim

(8)

2.3.2. Newton-Raphson Search Rule (NRSR)

The vectors are controlled by the NRSR, allowing for a more accurate

exploration of the viable region and obtaining better positions. The

NRSR is based on the notion that the NRM is presented to boost the

exploration tendency and speed up the convergence. Since numerous

optimization techniques are not differentiable, a mathematical NRM is

used to replace the explicit formulation of the function in such situa-

tions. The NRM begins with a presumed initial solution and proceeds to

the next location in a denite direction. In order to get the NRSR from

R. Sowmya et al.

评论收藏

内容反馈

版权申诉

电网论文源程序

粉丝: 1w+
资源: 369

220号资源-源程序：基于Newton-Raphson：一种新的基于群体的元启发式算法（附带WORD)-本人博客有解读

Newton-Raphson.rar_Newton-Raphson法_Newton–Raphson_Raphson_newton

Newton-raphson.rar_newton_newton-raphson

Newton-raphson-method.rar_Newton–Raphson_Raphson_newton_newton r

Newton-Raphson.rar_newton_newton raphson

Newton-Raphson法：Newton-Raphson算法的简单应用-matlab开发

基于MATLAB的Newton-Raphson法电力系统潮流计算.pdf

Newton-Raphson-Secant方法：使用Newton Raphson和Secant方法在多项式中找到根。-matlab开发

Newton-Raphson-power-flow.rar_newton_newton-raphson_潮流 C++_牛顿拉夫

Newton-Raphson 方法：Newton-Raphson 方法是一种迭代方法，用于寻找非线性方程及其系统的根。-matlab开发

newdim.zip_newton_newton-raphson

Newton-Raphson(C++).rar_newton_newton raphson_newton-raphson_牛顿拉

基于NEWTON-RAPHSON 方法进行潮流研究附matlab代码.zip

Newton-Raphson Loadflow

Newton-Raphson1:Newton-Raphson 方法的一种简单方法，用于求一个变量的方程根。-matlab开发

newton raphson

NEWTON-RAPHSON.rar_newton_newton-raphson

patb.rar_enjoy3b8_newton_newton-raphson_数学计算_非线性有限元

基于Newton-Raphson算法的电力系统潮流计算.pdf

基于MATLAB的Newton-Raphson法电力系统潮流计算.zip

NRO - Newton-Raphson One：NRO 是使用 Newton-Raphson 方法对一个变量求解方程的应用程序。-matlab开发

潮流分析工具箱：Polar Newton-raphson算法、笛卡尔坐标Newton-raphson算法、PQ算法-matlab开发

niudunfa.zip_newton_newton-raphson_泰勒法_牛顿法

newton.rar_load flow_newton_newton-raphson

Newton-Raphson 方法：Newton-Raphson 是一种求根算法，它可以连续生成对实值函数根的更好的近似。-matlab开发

Newton-iteration-method.rar_Newton-iteration_newton_newton itera

Newton-Raphson1:Newton-Raphson1 代码的修改。-matlab开发

Newton-Raphson-power-flow-program.rar_newton_power flow_power fl

最新资源